МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ОЦЕНКА НАДЕЖНОСТИ ХИМИЧЕСКОГО И НЕФТЯНОГО ОБОРУДОВАНИЯ ПРИ ПОВЕРХНОСТНОМ РАЗРУШЕНИИ
РД 26-10-87
Москва
1987
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН НИИхиммашем.
ИСПОЛНИТЕЛИ:
Р. Г. Маннапов, к. т. н., (руководитель темы); Е. Н. Гальперин, к. т. н.; В. Д. Жданов; Б. С. Вальтер; Г. Г. Дубровина.
2. УТВЕРЖДЕН Министерством
3. ВВЕДЕН В ДЕЙСТВИЕ письмом Главного технического управления от 28.08.87 г. № 11-10-4/1164.
4. ВВЕДЕН впервые.
5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ.
|
Обозначение НТД, на который дана ссылка |
Номер пункта, подпункта, перечисления, приложения |
|
ГОСТ 9.302-79 |
|
|
ГОСТ 9.908-85 |
|
|
ГОСТ 27.002-83 |
|
|
ГОСТ 27.003-83 |
|
|
ГОСТ 27.103-83 |
|
|
ГОСТ 27.502-83 |
РУКОВОДЯЩИЙ ДОКУМЕНТ ПО СТАНДАРТИЗАЦИИ
|
Методические
указания. |
РД |
Дата введения 01.01.88
Настоящий руководящий документ устанавливает метод оценки надежности химического и нефтяного оборудования, основной причиной нарушения работоспособности которого является сплошное поверхностное разрушение его элементов от воздействия технологических сред.
РД не распространяется на случаи локального разрушения оборудования.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Оценка надежности осуществляется путем проведения периодических обследований оборудования, измерения глубин разрушения его поверхностей, статистической обработки результатов измерений и последующего расчета показателей надежности.
1.2. При обследованиях должно быть установлено отсутствие коррозионного растрескивания, локальных видов коррозии (питтинга, щелевой, межкристаллитной), усиленной коррозии металла швов, зоны термического влияния и других видов локального разрушения оборудования, недопустимых при его эксплуатации, и наличие только сплошной коррозии, коррозии пятнами или коррозионно-эрозионного разрушения поверхностей оборудования.
1.3. Оценка надежности оборудования осуществляется по критериям его отказов и предельных состояний, устанавливаемых в технических условиях (стандартах ТУ) на оборудование в соответствии с ГОСТ 27.003-83 и ГОСТ 27.103-83 с целью достоверного определения его технического состояния (см. приложение 3 и п. 3.6).
1.4. При обследованиях должны быть определены площадь поверхности оборудования, подвергшейся разрушению; площадь поверхности, приходящейся на одно измерение (глубины разрушения или остаточной толщины стенки), в зависимости от выбранного метода измерений; степень неравномерности разрушения и необходимое число измерений (N). После измерений в N точках, равномерно распределенных по поверхности, осуществляются статистическая обработка результатов измерений (в соответствии с разделом 2) и оценка показателей надежности (в соответствии с разделом 3).
1.6. Методы статистической обработки результатов измерений глубин разрушения поверхностей следует применять для оценки степени разрушения больших поверхностей оборудования, находящихся в одинаковых условиях эксплуатации и разрушения, когда невозможно (или нецелесообразно) измерить глубину разрушения на всех участках обследуемой поверхности и измерения осуществляют выборочно. Для участков поверхности, находящихся в существенно различных условиях эксплуатации и разрушения (местные перегревы, повышенные скорости технологической среды и т.п.) применение статистических методов нецелесообразно, т. к. неравномерность разрушения будет определяться, главным образом, различием этих условий.
1.8. Термины, используемые в РД, соответствуют ГОСТ 27. 002-83.
1.9. Примеры применения методов статистической обработки и оценки надежности оборудования приведены в справочных приложениях 1 и 2.
1.10. Теоретические основы руководящего документа приведены в справочном приложении 3.
1.11. Обозначения, используемые в РД, приведены в справочном приложении 4.
2. МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
2.1. Статистическая обработка результатов измерений включает:
определение минимального необходимого числа измерений (объема выборки);
оценку однородности полученной выборки;
определение коэффициента вариации и параметров распределения глубин разрушения;
определение максимальной глубины разрушения с учетом масштаба поверхности.
2.2. Определение минимального числа точек поверхности для измерений.
2.2.1. Выбор необходимого минимального числа точек N поверхности для измерений следует осуществлять в соответствии с ГОСТ 27.502-83 по табл. 1 в зависимости от требуемой доверительной вероятности оценки g, допустимой ошибки d и степени неравномерности разрушения поверхности, характеризующейся коэффициентом вариации глубин разрушения uh.
2.2.2. Величина коэффициента вариации uh ориентировочно может быть выбрана
при малой неравномерности разрушений до 0,2
при значительной - » - 0,3 - 0,6
при сильной - » - 0,7 - 1,5
Таблица 1
Минимальное число N точек для измерений
|
g |
N при uh |
|||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,6 |
0,8 |
1,0 |
||
|
0,05 |
0,80 |
4 |
13 |
25 |
50 |
100 |
200 |
315 |
|
0,90 |
8 |
25 |
65 |
100 |
250 |
500 |
650 |
|
|
0,95 |
13 |
40 |
100 |
150 |
400 |
650 |
1000 |
|
|
099 |
25 |
100 |
200 |
315 |
800 |
1000 |
1000 |
|
|
0,10 |
0,80 |
- |
5 |
10 |
13 |
32 |
50 |
100 |
|
0,90 |
3 |
8 |
15 |
32 |
65 |
125 |
200 |
|
|
0,95 |
5 |
13 |
25 |
50 |
100 |
200 |
400 |
|
|
0,99 |
8 |
25 |
50 |
100 |
200 |
400 |
650 |
|
|
0,15 |
0,80 |
- |
3 |
5 |
6 |
15 |
25 |
40 |
|
0,90 |
- |
4 |
8 |
15 |
32 |
65 |
80 |
|
|
0 95 |
3 |
6 |
13 |
25 |
50 |
100 |
150 |
|
|
0,99 |
5 |
13 |
25 |
40 |
100 |
200 |
315 |
|
|
0,20 |
0,80 |
- |
- |
3 |
5 |
10 |
20 |
25 |
|
0,90 |
- |
4 |
6 |
10 |
20 |
40 |
50 |
|
|
0,95 |
- |
5 |
8 |
15 |
32 |
50 |
100 |
|
|
0,99 |
4 |
8 |
15 |
25 |
65 |
125 |
150 |
|
Примечание. Знак «-» означает, что число точек N < 3.
2.2.3. Доверительную вероятность g выбирают из ряда 0,80; 0,90; 0,95; 0,99.
2.2.4. Максимальную допустимую относительную ошибку d выбирают из ряда 0,05; 0,10; 0,15; 0,20.
2.2.5. Если по результатам N измерений получен коэффициент вариации больше заданного, то объем измерений уточняют в соответствии с п. 2.2.1. и выполняют дополнительные измерения.
2.3. При наличии в выборке резко выделяющихся значений hmax на участке, где получена величина hmax необходимо провести дополнительные измерения. В случае повторного появления такого значения принимается решение о несоответствии данного участка требованиям п. 1.5 и необходимости оценки его надежности отдельно от всей обследуемой поверхности.
Критерием резкого выделения значения hmax из выборки является выполнение условия
![]()
где коэффициент вариации uh и средняя глубина
разрушения ![]() вычисляются по п. 2.4.
без учета значения hmax.
вычисляются по п. 2.4.
без учета значения hmax.
2.4. Определение коэффициента вариации глубин разрушения по поверхности, uh.
2.4.1. Вычисляют среднюю глубину разрушения:
2.4.2. Вычисляют среднее квадратическое отклонение глубин разрушения:
где D - предельная ошибка метода измерений.
2.4.3. Вычисляют коэффициент вариации глубин разрушения:
2.4.4. Уточняют N в соответствии с п. 2.2.5.
2.5. Определение параметров распределения глубин разрушения.
2.5.1. Параметры распределения определяются для функции Вейбулла:
![]() (4)
(4)
где а - параметр масштаба; b - параметр формы.
Теоретическое обоснование см. в приложении 3.
2.5.2. Параметр масштаба «а» определяется по средней глубине разрушения:
где Kb - коэффициент, зависящий от uh, определяется по табл. 2.
2.5.3. Параметр формы «b» определяется по коэффициенту вариации uh по табл. 2.
Таблица 2
Взаимосвязь параметров b, кb и u распределения Вейбулла
|
Kb |
u |
|
|
0,8 |
1,133 |
1,261 |
|
0,9 |
1,52 |
1,113 |
|
1,0 |
1,000 |
1,000 |
|
1,1 |
0,965 |
0,910 |
|
1,2 |
0,941 |
0,837 |
|
1,3 |
0,924 |
0,775 |
|
1,4 |
0,911 |
0,723 |
|
1,5 |
0,903 |
0,679 |
|
1,6 |
0,897 |
0,640 |
|
1,7 |
0,892 |
0,605 |
|
1,8 |
0,889 |
0,575 |
|
1,9 |
0,887 |
0,547 |
|
2,0 |
0,886 |
0,523 |
|
2,1 |
0,886 |
0,500 |
|
2,2 |
0,886 |
0,480 |
|
2,3 |
0,886 |
0,461 |
|
2,4 |
0,887 |
0,444 |
|
2,5 |
0,887 |
0,428 |
|
2,6 |
0,888 |
0,413 |
|
2,7 |
0,889 |
0,399 |
|
2,8 |
0,890 |
0,386 |
|
2,9 |
0,892 |
0,375 |
|
3,0 |
0,893 |
0,363 |
|
0,894 |
0,353 |
|
|
3,2 |
0,896 |
0,343 |
|
3,3 |
0,897 |
0,334 |
|
3,4 |
0,898 |
0,325 |
|
3,5 |
0,900 |
0,316 |
|
3,6 |
0,901 |
0,309 |
|
3,7 |
0,902 |
0,301 |
|
3,8 |
0,904 |
0,294 |
|
3,9 |
0,905 |
0,287 |
|
4,0 |
0,906 |
0,281 |
|
4,5 |
0,913 |
0,253 |
|
5,0 |
0,918 |
0,230 |
|
6,0 |
0,928 |
0,194 |
|
7,0 |
0,935 |
0,168 |
|
8,0 |
0,942 |
0,148 |
|
9,0 |
0,947 |
0,133 |
|
10,0 |
0,951 |
0,120 |
|
12,0 |
0,958 |
0,101 |
|
14,0 |
0,964 |
0,087 |
|
16,0 |
0,969 |
0,077 |
|
18,0 |
0,971 |
0,069 |
|
20,0 |
0,974 |
0,0625 |
|
25,0 |
0,978 |
0,0510 |
2.6. Определение максимальной глубины разрушения на обследуемой поверхности.
(Теоретическое обоснование см. в приложении 3).
2.6.1. Максимальная глубина разрушения при возможности измерения на всех участках обследуемой поверхности определяется путем непосредственного измерения.
где g - требуемая достоверность оценки;
М = S/S0 - показатель масштаба;
S - площадь поверхности, подлежащей обследованию;
S0 - площадь поверхности, приходящаяся на одно независимое измерение.
2.6.3. Величина S0 определяется по среднему числу «n» каверн (язв, впадин или выступов), приходящихся на единицу поверхности, S0 = 1/n.
2.6.4. Глубину разрушения (hb) на доле поверхности b, определяют по формуле
2.7. Пример применения статистических методов приведен в приложении 1.
3. ОЦЕНКА НАДЕЖНОСТИ ОБОРУДОВАНИЯ
показатели долговечности - средний ресурс (срок службы) и установленный ресурс (срок службы);
показатели безотказности - средняя наработка до отказа (либо на отказ), установленная безотказная наработка или вероятность безотказной работы.
Средний ресурс (срок службы, наработка до отказа) - математическое ожидание ресурса (срока службы, наработки до отказа).
Установленный ресурс (срок службы, наработка до отказа) - значение ресурса (срока службы, наработки до отказа), обеспечиваемое с заданной вероятностью, близкой к единице.
3.2. Расчет осуществляют по параметрам распределения глубин разрушения, приведенным к заданному моменту времени (экстраполяцией по времени).
3.4. При известном виде закономерности изменения средней глубины разрушения от времени h(t) необходимое число обследований уменьшается до числа неизвестных коэффициентов функции h(t), которые определяются по результатам обследований.
В частном случае, когда известно, что зависимость глубины разрушения от времени линейна: h(t) = c1 + c2t, для оценки неизвестных коэффициентов «с1» и «с2» достаточно двух обследований или (при c1 = 0) одного обследования.
3.5. Параметры распределения глубин разрушения для заданного момента времени t определяются в соответствии с п. 2.5, причем значение средней глубины разрушения ht определяется по функции h(t), а коэффициент вариации uht по формуле:
где uh - коэффициент
вариации, соответствующий средней глубине разрушения ![]() .
.
3.6. Показатели надежности рассчитываются по следующим критериям.
Показатели долговечности (срок службы, ресурс) - по критерию разрушения установленной доли (b) поверхности на предельно допустимую глубину hпред (величину прибавки на коррозию и другие запасы).
Показатели безотказности (наработка до отказа, вероятность безотказной работы) - по достижению глубины разрушения (hmax) в одной из точек поверхности толщины H стенки аппарата (или покрытия).
3.7. Расчет показателей долговечности.
3.7.1. Расчет среднего ресурса (срока службы) Тр.
Расчет ведется путем решения относительно t уравнения
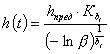 , (9)
, (9)
где «bt» и «Kbt» определяются по табл. 2 в зависимости от uht, определяемого по формуле
где hb определяется по результатам обследования по формуле (7);
uh - коэффициент вариации, соответствующий hb.
В частном случае, при постоянной скорости разрушения «с»:
3.7.2. Расчет установленного ресурса (срока службы), Тру, осуществляют по формуле:
где Тр определяется по п. 3.7.1;
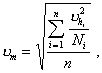 (13)
(13)
где n - число обследований;
uhi - коэффициент вариации, определенный при i-м обследовании по результатам Ni измерений , приведенный по формуле (8) к моменту tn.
В частном случае, когда число обследований равно 1,
3.8. Расчет показателей безотказности.
3.8.1. Расчет средней наработки до отказа Т0.
Расчет выполняют путем решения относительно t уравнения
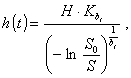 (15)
(15)
где S0 и S определены в п. 2.6;
«bt» и «Kbt» определяют по табл. 2 в зависимости от uht:
hmax определяется по результатам обследования по формуле (6);
uh - коэффициент вариации, соответствующий hmax.
В частном случае, при постоянной скорости разрушения «с»:
3.8.2. Расчет установленной безотказной наработки T0y осуществляют по формуле:
где T0 определяется по п. 3.8.1;
uт - определяется по п. 3.7.2.
3.8.3. Расчет вероятности безотказной работы Р(t) осуществляют по формуле:
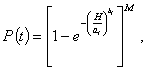 (19)
(19)
где at, bt - параметры распределения, определенные для момента времени t в соответствии с п. 3.5;
M - по п. 2.5.2.
3.9. Пример оценки показателей надежности приведен в приложении 2.
3.10. При малой глубине разрушений поверхностей оборудования, не превышающей предельной ошибки D метода измерений, подтверждение показателей надежности, записанных в нормативно-технической документации, может быть осуществлено по нижним границам показателей, определяемых по формулам:
![]()
где t0 - продолжительность эксплуатации до момента обследования (не менее 1 года).
ПРИЛОЖЕНИЕ 1
Справочное
ПРИМЕР ПРИМЕНЕНИЯ СТАТИСТИЧЕСКИХ МЕТОДОВ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ ГЛУБИН РАЗРУШЕНИЯ
При обследовании резервуара для хранения нефтепродуктов после пяти лет эксплуатации необходимо было определить максимальную глубину разрушения стенок верхнего пояса, подвергающегося наибольшей коррозии, а также глубину разрушения, которая превышает 5 % поверхности. Площадь поверхности верхнего пояса составляет 100 м2.
Предварительный осмотр показал, что стенки резервуара подверглись сплошной коррозии малой неравномерности.
Решение.
1. Выбор минимального числа измерений осуществляем по табл. 1, для чего задаемся максимально допустимой относительной ошибкой d = 0,10 и доверительной вероятностью оценки g = 0,95. Коэффициент вариации в соответствии с п. 2.2.2 принимаем равным 0,2. По табл. 1 определяем N = 13.
2. После измерений в 13 равноудаленных точках поверхности верхнего пояса остаточной толщины стенок (с помощью ультразвукового толщиномера) получены следующие значения глубин разрушения, мм: 1,3; 1,2; 1,5; 1,4; 1,0; 1,1; 1,4; 1,6; 1,2; 1,4; 2,0; 1,7; 1,4.
3. По формуле (1) определяем среднюю глубину разрушения:
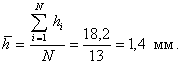
4. По формуле (2) определяем среднее квадратическое отклонение глубин разрушения:
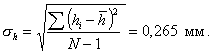
5. По формуле (3) определяем коэффициент вариации:
![]()
Так как полученное значение коэффициента вариации меньше выбранного, то дополнительных измерений не требуется.
6. По табл. 2, используя интерполяцию,
определяем параметр формы распределения глубин разрушения b = 6,1 и коэффициент Kb = 0,93, по
которому вычисляем параметр масштаба ![]()
7. Для расчета максимальной глубины разрушения по формуле (6) определим
![]()
где S0 - поверхность, приходящаяся на одно независимое измерение толщиномера S0 = 0,5 см2 = 0,5·10-4 м2.
По формуле (6) определяем максимальную глубину разрушения поверхности для выбранной доверительной вероятности g =0,95:
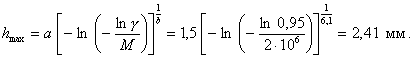
Видим, что подученная величина hmax несколько выше, чем максимальная из измеренных величин - 2,0 мм.
8. Глубину hb на 5 % поверхности (b = 0,05), определяем по формуле (7)
![]()
ПРИЛОЖЕНИЕ 2
Справочное
ПРИМЕР ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
По данным предыдущего примера необходимо оценить показатели надежности резервуара: средний и установленный срок службы, среднюю и установленную безотказную наработку. Толщина стенок резервуара Н = 10 мм. Критерий предельного состояния - разрушение 5 % поверхности на глубину (hпред) более 4 мм.
По многолетним данным
эксплуатации известно, что зависимость средней глубины коррозии стенок
резервуаров от времени имеет вид ![]()
Решение.
1. Расчет среднего срока службы резервуара до наступления предельного состояния по формуле (11).
1.1. Определяем среднюю скорость коррозии:
![]()
1.2. По формуле (10) определяем коэффициент вариации, соответствующий моменту наступления предельного состояния
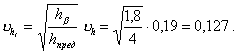
1.3. По табл. 2 определяем bt =9,5, Kbt = 0,95.
1.4. По формуле (11) определяем Тр:
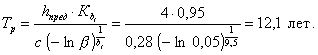
2. Расчет установленного срока службы Тpy осуществляем по формуле (12).
2.1. По формуле (14) определяем коэффициент вариации ресурса
![]() .
.
2.2. Определяем Трy
![]()
3. Расчет средней наработки до отказа осуществляем по критерию возникновения сквозного разрушения стенки по формуле (17).
3.1. По формуле (16) определяем коэффициент вариации глубин разрушения, соответствующий моменту сквозного разрушения:
![]()
3.2. По табл. 2 определяем bt =13; Кbt = 0,96.
3.3. По формуле (17) определяем Т0:
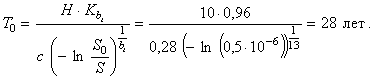
4. Установленную безотказную наработку T0y определяем по формуле (18):
![]()
Таким образом в данном случае предельное состояние резервуара (Tpy =10,2 лет) наступит раньше, чем возникнут его отказы (сквозные разрушения).
При большей неравномерности коррозионного разрушения (при большем значении uh) сквозные разрушения оболочек могут возникнуть раньше, чем наступит предельное состояние. По данным рассмотренного примера такой случай наступил бы при величине uh ³ 0,7.
ПРИЛОЖЕНИЕ 3
Справочное
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РУКОВОДЯЩЕГО ДОКУМЕНТА
Химическое и нефтяное оборудование при эксплуатации подвергается различным видам разрушения, в том числе поверхностному коррозионному и эрозионному разрушению от воздействия технологических сред.
При периодических обследованиях осуществляют измерения степени разрушения элементов оборудования, на основе которых делают заключение о возможности дальнейшей эксплуатации оборудования и прогнозируют сроки его службы до предельного состояния. Величины поверхностей оборудования (например, оболочек) достигают десятков и сотен квадратных метров, поэтому измерить глубину разрушения во всех точках (участках) этих поверхностей практически невозможно. В связи с этим измерение глубин разрушения осуществляют выборочно, в местах подвергающихся наибольшему разрушению. В тех случаях, когда такие места легко выявляются и известны причины повышенной скорости разрушения (повышенные скорости, температуры, концентрации технологической среды и др.), указанный подход оказывается эффективным. Если же условия эксплуатации для всех участков обследуемой поверхности одинаковы, а неравномерность глубин разрушения в различных точках поверхности существенна, необходим статистический подход к оценке степени разрушения оборудования.
При традиционном подходе по результатам измерений определяют среднюю глубину разрушения поверхности и максимальную глубину, не оценивая достоверности полученных результатов. Такой подход в некоторых случаях может привести к большим ошибкам.
Величина ошибки зависит от числа точек (участков) поверхности, в которых проводились измерения, площади обследуемой поверхности, степени неравномерности величины разрушения по поверхности.
Неравномерность коррозионного разрушения поверхностей металлов в различных точках при одинаковых внешних условиях обусловлена неоднородностью физико-химических свойств реальных металлов и сплавов, проявляющаяся в их электрохимической гетерогенности. По современным воззрениям*) электрохимическая гетерогенность поверхности металла может быть вызвана микронеоднородностью структуры металла как, например, различием в составе или ориентации отдельных кристаллов, наличием границ зерен и инородных включений, и субмикронеоднородностью металла (местные несовершенства кристаллической решетки вследствие дислокации или включения других атомов в решетку основного металла). Поэтому, если важно определение не только величины общего коррозионного эффекта, но и расчет распределения коррозионного поражения по поверхности, то единственно правильным считается (Томашов Н. Д., Чернова Г. П., Теория коррозии и коррозионностойкие сплавы. М.: Металлургия, 1986) рассмотрение процесса коррозии с привлечением гетерогенно-электрохимического механизма. При этом применение вероятностно-статистических методов является необходимым.
*) Я. М. Колотыркин. Металл и коррозия. М.: Металлургия, 1985.
Вопросами статистического анализа коррозионного разрушения оборудования в последнее время начали заниматься также зарубежные специалисты-коррозионисты. Так, например, этим вопросам посвящена работа авторов J. E. Strutt, J. R. Nicholls and B. Barbier «The prediction of corrosion by statistical analysis of corrosion profiles» (Corrosion science, 1985, Volume 25, No. 5, p. 305 - 316), в заключении которой говорится:
1. Применение статистических методов при исследовании прокорродировавших поверхностей обеспечивает более точную оценку возникающей степени коррозии, когда профиль поверхности является неоднородным. Для прогнозирования коррозии успешно может быть использовано распределение экстремальных значений, когда полное распределение глубин не может быть описано никаким из хорошо известных распределений.
2. Профилометрирование поверхностей и статистический анализ, редко используется в коррозионных исследованиях, но может быть крайне полезным для морфологических коррозионных исследований, дополняя применяющиеся коррозионистами методы.
3. Экспериментальные данные, приведенные в данной статье, показали, что зависимость статистических параметров от времени является важной при оценке долговечности сталей и может указать на механизм коррозии.
К п. 1.3. и 3.6
КРИТЕРИИ ОТКАЗОВ И ПРЕДЕЛЬНЫХ СОСТОЯНИЙ ОБОРУДОВАНИЯ ПРИ ПОВЕРХНОСТНОМ РАЗРУШЕНИИ
В соответствии с ГОСТ 27.003-83 и ГОСТ 27.103-83 критерии отказов и предельных состояний изделий должны устанавливаться в технических условиях (стандартах ТУ) с целью достоверного определения их технического состояния.
Критерии отказа - это совокупность признаков, характеризующих неработоспособное состояние изделия. Критерием предельного состояния является совокупность признаков, при которых использование по назначению должно быть прекращено (или невозможно) и изделие должно направляться в капитальный ремонт или списываться (сниматься с эксплуатации).
Предельным состоянием оборудования, подвергающегося при эксплуатации коррозионно-эрозионному разрушению, является уменьшение толщины его стенок до предельной величины, ниже которой не обеспечивается необходимый запас его несущей способности.
Глубина отдельных локальных разрушений (исключая трещины) может значительно превышать среднюю глубину разрушения (вплоть до сквозного разрушения) и не нарушать несущей способности аппарата. Однако появление сквозных разрушений нарушает работоспособность аппаратов, т. е. является критерием их отказов, а если работоспособность аппаратов после таких отказов не подлежит восстановлению, то и критерием их предельного состояния.
Кроме того для высоконагруженного оборудования возникновение даже отдельных дефектов поверхности может явиться причиной возникновения и развития трещин. Поэтому для такого оборудования должна устанавливаться предельно допустимая величина поверхностных дефектов, которая является критерием его предельного состояния.
Таким образом при оценке надежности оборудования, подвергающегося коррозионно-эрозионному разрушению, в качестве предельного состояния оборудования принимается разрушение определенной доли (b) поверхности на предельно допустимую глубину (величину прибавки на коррозию и другие запасы).
В качестве критерия отказа принимается возникновение сквозного разрушения стенки аппарата (или покрытия), что соответствует достижению глубины (hmax) разрушения в одной из точек поверхности толщины стенки аппарата или покрытия. Этот критерий одновременно является и критерием предельного состояния оборудования, если после отказа его восстановление невозможно или нецелесообразно.
К разделу 2
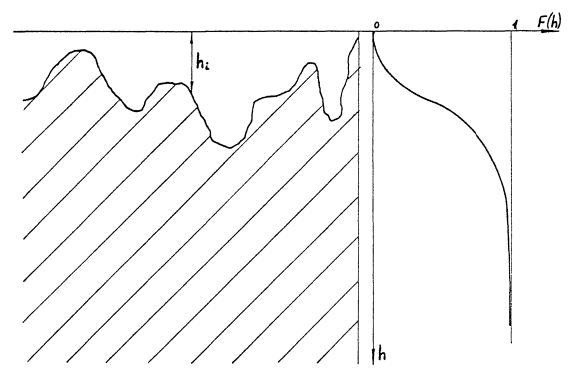
Неравномерность разрушения поверхности характеризуется функцией распределения глубин разрушения F(h), см. черт. 1. Числовое значение этой функции определяет долю поверхности, имеющей глубину разрушения меньше, чем h.
Специальные исследования (Отчет № гос. рег. 01840031823 «Разработка рекомендаций по выбору материалов с учетом требований надежности». М.: НИИхиммаш, 1985) показали, что распределение глубин разрушения по поверхности подчиняется закону Вейбулла (без сдвига), функция которого имеет вид:
![]() (1)
(1)
где а - параметр масштаба распределения, определяемый по средней глубине разрушения;
b - параметр формы, характеризующий разброс значений h.
Параметр формы определяется по коэффициенту вариации (см. табл. 2), значения которого зависят от вида разрушения.
При оценке степени разрушения оборудования и прогнозировании его надежности необходимое определять максимальную глубину разрушения hmax. Величина hmax при прочих равных условиях зависит от площади поверхности, подвергающейся разрушению. Доказательство этого факта приведено в работе Новаковского В. М. «К стандартной научной системе коррозионно-электрохимических понятий и терминов», опубликованной в ж. «Защита металлов», т. 16, № 3, 1980, с. 250 - 264.
Выведем формулу для расчета hmax. В соответствии с формулой (1) для максимально допустимой величины разрушения hmax вероятность ее непревышения при измерении на единичном участке поверхности S0 будет равна:
![]() (2)
(2)
На «М» участках поверхности вероятность h < hmax будет равна:
Функция распределения F(h) глубин разрушения поверхности
Черт. 1.
Для поверхности площадью S величина М = S/S0.
Зависимость (3) положена в основу расчета вероятности безотказной работы поверхности по критерию непревышения глубины ее разрушения предельно допустимой величины.
Подстановкой в формулу (3) заданной достоверности оценки g = F(hmax), получим выражение для расчета максимальной глубины разрушения на поверхности заданной площади:
Величина М = S/S0 зависит как от площади обследуемой поверхности S, так и от величины поверхности S0, приходящейся на одно измерение.
Величина S0 зависит от вида инструмента, используемого для измерений глубины разрушения. Например, если глубина разрушения определяется путем измерения остаточной толщины стенки оборудования ультразвуковым толщиномером, то площадь измеряемого участка поверхности будет равна площади контакта измерительной головки с измеряемой стенкой. При измерении щуповыми инструментами площадь определяется площадью сечения щупа. Минимальное значение, которое может принимать величина S0, определяется радиусом корреляции глубин разрушения по поверхности металла. Как установлено в работе (Отчет № гос. рег. 01840031823) величина этого радиуса составляет до 1 - 2 величин среднего размера зерен металла и может быть ограничена величиной порядка 0,1 мм2.
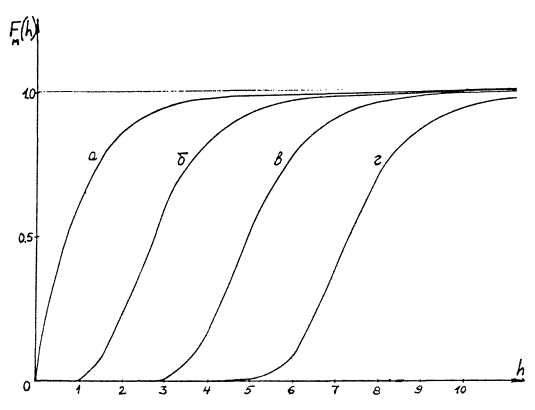
На черт. 2 показаны функции распределения, построенные с использованием формулы (4) при некоторых значениях «М». Видим, что с возрастанием площади «М» поверхности математическое ожидание максимальной глубины разрушения увеличивается, а разброс ее значений уменьшается.
Указанное свойство уменьшения разброса максимальных значений с увеличением М может быть использовано для резкого уменьшения числа необходимых измерений (то есть уменьшения их трудоемкости) при обеспечении требуемой точности результатов. Это возможно в тех случаях, когда максимальная глубина разрушения на некотором участке поверхности легко выявляется визуально.
Функции распределения максимумов FM(h) из М значений:
а) исходная функция (М = 1); б) М = 10; в) М = 100; г) М = 1000.
Черт. 2.
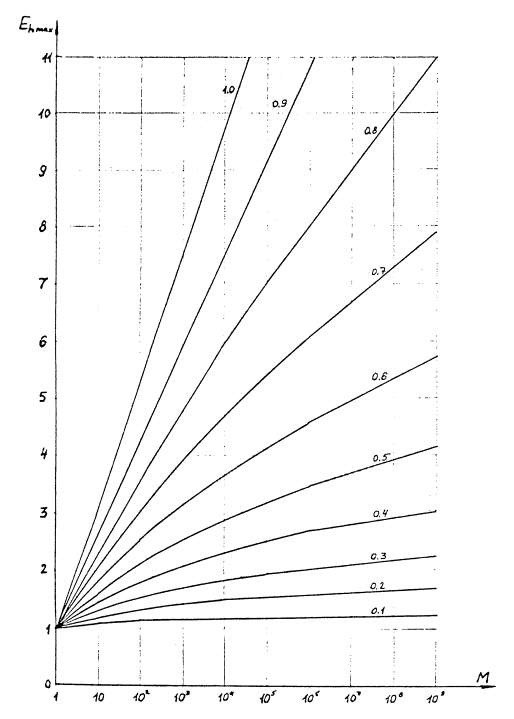
Зависимость математического ожидания максимума от числа М значений случайной величины, распределенной по закону Вейбулла. Величины коэффициентов вариации исходных распределений указаны около кривых.
Черт. 3.
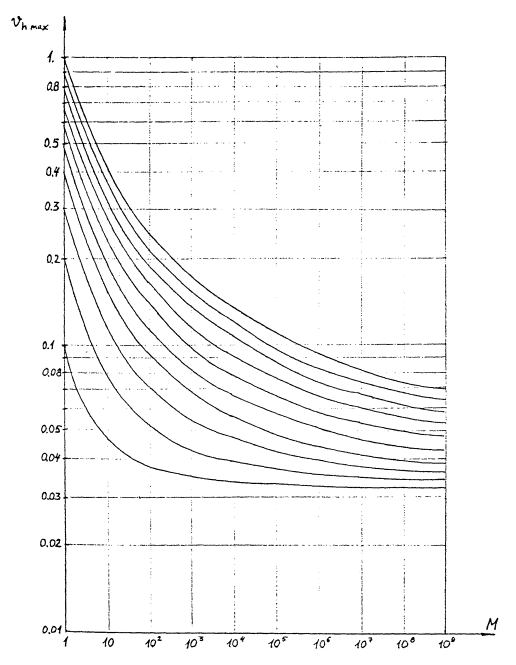
Зависимость коэффициента вариации максимума от числа М значений случайной величины, распределенной по закону Вейбулла
Черт. 4.
На черт. 3 и 4 представлены зависимости математического ожидания и коэффициента вариации максимума из М значений величины, распределенной по закону Вейбулла.
При использовании приведенных зависимостей достаточно измерить максимальную глубину разрушения на нескольких участках известной площади (М по п. 2.6.2) и определить (по п. 2.4) коэффициент вариации этих глубин.
По полученным данным на черт. 4 определяется кривая, соответствующая данному виду разрушения, и на черт. 3 может быть определена максимальная глубина разрушения для поверхности любой площади.
Расчет hmax по формуле (4) при больших
значениях М неудобен, поэтому сделаем замену ![]() , которая при М > 10 дает ошибку меньше 1 %, при М
> 100 - 0,1 % и т. д. Получаем более удобную для расчетов формулу (см. п. 2.6.2):
, которая при М > 10 дает ошибку меньше 1 %, при М
> 100 - 0,1 % и т. д. Получаем более удобную для расчетов формулу (см. п. 2.6.2):
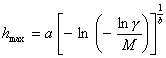 .
.
Эта формула положена в основу критерия
резкого выделения значения hmax из выборки (п. 2.3).
Значение уровня значимости a принято равным 0,05 (g = 1 - a),
значение 1/b » u
(погрешность в пределах 15 %), значение ![]() (погрешность до 10
%). Получаем более простую формулу, удобную для предварительной оценки:
(погрешность до 10
%). Получаем более простую формулу, удобную для предварительной оценки:
![]()
Расчет показателей долговечности оборудования осуществляют по критерию разрушения установленной доли (b) поверхности на предельно допустимую глубину (hпред). В этом случае предельному состоянию оборудования соответствует условие hb = hпред, где hb - глубина разрушения, которую имеет или превышает доля поверхности b.
Величины b и hb связаны между собой через функцию распределения (1):
![]()
откуда
![]() (5)
(5)
Формула (5) использована в п. 2.6.4.
Определим параметры распределения, соответствующие предельному состоянию: hb = hпред.
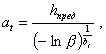
где bt - соответствует коэффициенту вариации в момент наступления предельного состояния ut.
Выражая параметр формы через среднее значение функции (at = ht/Kbt), получаем уравнение связи между средним и предельным значениями глубины разрушения:
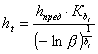 . (6)
. (6)
Из этого уравнения по известной функции h(t) можно найти время Тр (срок службы) до предельного состояния поверхности. В частном случае, когда h(t) = c · t, срок службы
Поскольку коэффициенты «Kbt» и «bt», определяемые по ut, зависят от времени, уравнения (6, 7) могут быть решены с заранее заданной точностью лишь путем последовательных приближений по функции u(t).
В результате специально проведенных исследований (Маннапов Р. Г. «Оценка надежности аппаратов в условиях поверхностного разрушения технологическими средами», ж. «Химическое и нефтяное машиностроение», 1987, № 5) установлен вид зависимости коэффициента вариации (uht) от средней глубины разрушения (ht):
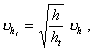 (8)
(8)
где uh - коэффициент вариации, соответствующий средней глубине разрушения h.
Заменяя в (8) подкоренное выражение, получаем формулы, приведенные в п. 3.7. и 3.8:
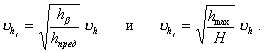
Эти формулы дают несколько завышенное значение uht, что обеспечивает запас надежности (1 - 3 %) при расчете. При необходимости более точного расчета используют метод последовательных приближений.
Вероятность безотказной работы по критерию отсутствия сквозных разрушений или нарушения сплошности покрытия за требуемый срок службы t определяется путем подстановки в формулу (3) значения hmax = H.
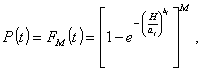
где параметры at и bt соответствуют заданному сроку службы.
Расчет установленного ресурса (наработки) осуществляется в соответствии с рекомендациями МР 88-83 «Надежность в технике. Методы оценки и контроля индивидуальных показателей надежности» (М.: ВНИИНМАШ, 1983), согласно которым для нормального распределения
![]()
где Т - средний ресурс, s - среднее квадратическое отклонение ресурса, uт - коэффициент вариации ресурса.
Правомерность применения нормального распределения для оценки доверительных интервалов математического ожидания величины, распределенной по любому двухпараметрическому закону, указана в ГОСТ 27.503-81 «Надежность в технике. Система сбора и обработки информации. Методы оценки показателей надежности».
Коэффициент вариации прогнозируемой величины ресурса uт при условии сохранения режима (условий) эксплуатации и соответствующей закономерности разрушения зависит от числа значений измеряемых параметров, т. е. числа обследований n и числа измерений Ni при каждом обследовании:
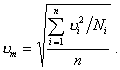
ПРИЛОЖЕНИЕ 4
Справочное
ОБОЗНАЧЕНИЯ, ПРИМЕНЯЕМЫЕ В РД
Обозначения приведены в порядке упоминания в РД.
N - число измерений;
g - доверительная вероятность;
d - допустимая ошибка;
uh - коэффициент вариации глубин разрушения;
![]() - средняя
измеренная глубина разрушения;
- средняя
измеренная глубина разрушения;
hmax - максимальная глубина разрушения;
hi - измеренная случайная глубина разрушения;
sh - среднее квадратическое отклонение глубин разрушения;
F(h) - функция распределения глубин разрушения;
а - параметр масштаба функции распределения;
b - параметр формы функции распределения;
Кb - параметрический коэффициент распределения Вейбулла;
М - показатель масштаба поверхности;
S - площадь поверхности оборудования, подвергшаяся разрушению;
S0 - площадь поверхности, приходящаяся на одно измерение;
hb - глубина разрушения на доле поверхности b;
h(t) - функция изменения средней глубины разрушения от времени;
t - время эксплуатации (ресурс);
c1, с2 - коэффициенты в зависимости h(t).
ht - средняя глубина разрушения, соответствующая времени t;
uht - коэффициент вариации глубин разрушения в момент времени t;
hпред - предельно допустимая глубина разрушения;
Н - толщина стенки (или покрытия);
Т - средний ресурс (срок службы, наработка);
bt - параметр формы распределения глубин разрушения, соответствующий моменту t.
Kbt - коэффициент, соответствующий bt;
Ty - установленный ресурс;
uт - коэффициент вариации ресурса;
ui - коэффициент вариации, определенный при i-м обследовании по результатам Ni измерений;
n - число обследований;
Р(t) - вероятность безотказной работы за период до момента (t);
a - уровень значимости события hi > hmax.
СОДЕРЖАНИЕ
|
2. Методы обработки результатов измерений. 2 3. Оценка надежности оборудования. 5 Приложение 2 Пример оценки показателей надежности. 8 |
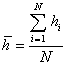
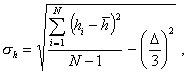
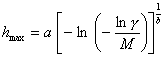 ,
,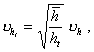
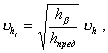
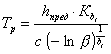
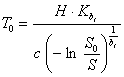
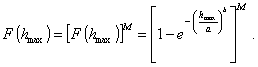
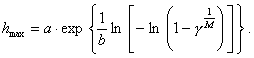
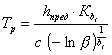 .
.