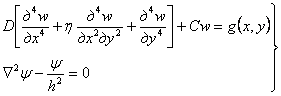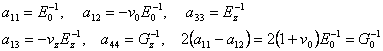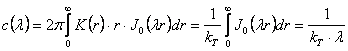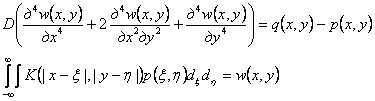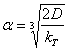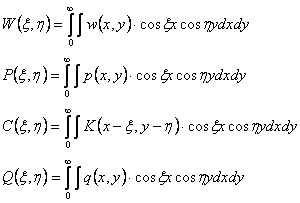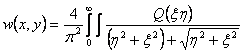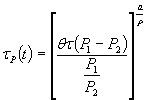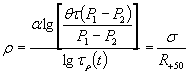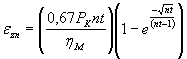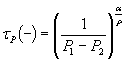МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
СБОРНИК НАУЧНЫХ ТРУДОВ
МОСКВА 1999
СОДЕРЖАНИЕ
Издание МАДИ (ТУ), 1999, 94 с, 19 рис., 4 табл., 60 библ.
В сборнике научных трудов приведены результаты теоретических и экспериментальных исследований в области проектирования, организации строительства и оптимизации элементов конструкций аэродромных сооружений.
Сборник предназначен для инженеров и специалистов, работающих в области проектирования и строительства аэропортов, а также для студентов, обучающихся по специальности 29.10 «Строительство автомобильных дорог и аэродромов».
Редакционная коллегия:
д-р техн. наук, проф. А.П. Степушин (отв. ред.),
д-р техн. наук, проф. Г.И. Глушков,
д-р техн. наук, проф. Г.И. Попов,
канд. техн. наук, доц. В.Д. Агеев,
канд. техн. наук, ст. науч. сотр. С.В. Картошина (отв. секретарь)
ПРЕДИСЛОВИЕ
Публикуемые в настоящем сборнике научных трудов материалы теоретических и экспериментальных исследований посвящены совершенствованию теории расчета конструкций аэродромных покрытий и обеспечению требуемой надежности на стадиях проектирования и строительства.
В статье А.П. Степушина и В.А. Сабуренковой приведена математическая модель вероятностного расчета конструкций жесткого аэродромного покрытия из цементобетона с заданным уровнем надежности.
В статье Г.И. Глушкова и С.В. Картошиной рассмотрены аспекты повышения точности существующего нормативного метода расчета на основе учета различных условий на контакте покрытия и анизотропного основания.
Вопросы совершенствования метода расчета бетонных покрытий рассмотрены в статье А.И. Юрченко.
Статьи Г.И. Попова, Г.И. Филимошкиной, И.Е. Марьясиной посвящены совершенствованию теории расчета железобетонных элементов.
Вопросы применения новых строительных материалов, организации строительства рассмотрены С.С. Ловшиным, В.А. Серебренниковым, А.В. Агеевым.
В работе О.В. Елфимовой рассмотрены аспекты, связанные с оптимизацией генерального плана аэропорта.
Д-р. техн. наук, проф. А.П. Степушин
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Д-р техн. наук, проф. А.П. Степушин,
канд. техн. наук В.А. Сабуренкова
КОНЦЕПЦИЯ СИСТЕМНОГО ПОДХОДА К ОБЕСПЕЧЕНИЮ ТРЕБУЕМОЙ НАДЕЖНОСТИ ЦЕМЕНТОБЕТОННОГО ПОКРЫТИЯ
В настоящее время при проектировании конструкций аэродромных покрытий применяют детерминированные методы расчета плит на упругом основании. Процедура расчета жесткого покрытия сводится к оценке двух - трех вариантов конструкций, соответствующих заданной нормативной нагрузке на основную опору расчетного воздушного судна (или категории нормативной нагрузки), с проверкой условия
|
md ≤ mu |
(1) |
где md и mu - соответственно величины расчетного и предельного изгибающих моментов, Применяемое в результате расчета сравнение вариантов конструкций покрытий по единственному критерию - приведенным затратам на их сооружение - без оценки надежности принятых решений на стадии проектирования не обеспечивает выбора оптимальных решений, так как при этом игнорируются следующие аспекты: вероятностно-статистические закономерности распределения эксплуатационных нагрузок от колес воздушных судов и температуры, прочностных и деформационных характеристик материалов, а также геометрических характеристик конструктивных слоев жесткого аэродромного покрытия.
Дальнейшее совершенствование методики расчета и обеспечения требуемой надежности аэродромных и дорожных покрытий на стадии проектирования возможно на основе использования методологии системного подхода, центральной процедурой которого является построение обобщенной модели инженерной конструкции или сооружения.
Разработке обобщенной модели конструкции жесткого аэродромного покрытия посвящена работа В.Е. Тригони /1/, в которой предусмотрен учет надежности принимаемого решения конструкции цементобетонного (армобетонного) покрытия введением коэффициента условий работы, предложенного В.Д. Садовым и учитывающего изменчивость лишь двух факторов: прочности цементобетона на растяжение при изгибе и величины температурных напряжений в цементобетоне. При этом не учитывается стохастическая природа таких входных переменных, как деформационные характеристики грунтовых и искусственных оснований, взлетные массы воздушных судов, распределение нагрузок от колес главных опор по ширине участков аэродромных покрытий и геометрические характеристики конструктивных слоев.
В связи с этим одной из актуальных задач развития обобщенной модели системного подхода к проектированию искусственных покрытий аэродромов и дорог является усовершенствование модели подсистемы оценки надежности жестких одежд с учетом перечисленных факторов.
Ниже приведена блок-схема предлагаемой модели подсистемы оценки надежности жесткого аэродромного покрытия на стадии проектирования (рис.).
Модель подсистемы оценки надежности включает систему входных параметров:
нагрузки от воздушных судов, важнейшими характеристиками которых являются: взлетная масса воздушного судна, количество главных опор, доля взлетной массы, приходящаяся на главные опоры, число и схема компоновки колес на главной опоре и давление в шинах; расчетное число приложений нагрузки за проектный срок службы;
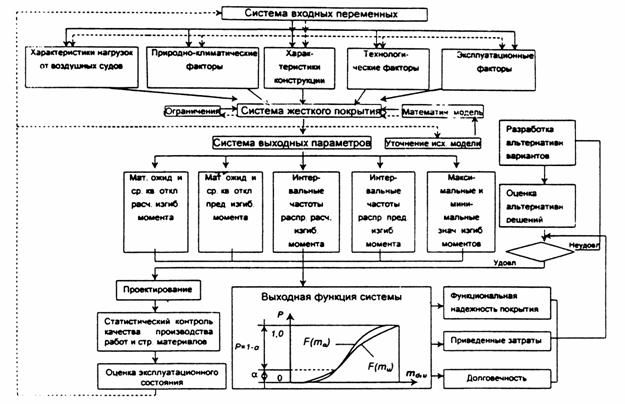
Рис Блок-схема к расчету жесткого аэродромного покрытия с заданным уровнем надежности
природно-климатические факторы: годовая амплитуда среднесуточных температур воздуха, интенсивность солнечной радиации, среднесуточная амплитуда колебания температуры на поверхности цементобетона, ее повторяемость и коэффициент вариации, число переходов температуры через ноль в году, влажность и глубина сезонного промерзания грунта и высотное положение грунтовых вод;
характеристики конструкции покрытия: толщина, ширина и длина плиты, наличие и тип стыковых соединений, изолирующих прослоек, прочностные и деформационные характеристики материалов: класс и коэффициент вариации прочности цементобетона на растяжение при изгибе, начальный модуль упругости цементобетона, коэффициент постели грунта искусственного основания;
технологические факторы: минимальная и максимальная толщина конструктивных слоев, отклонение толщин конструктивных слоев от проектных, обусловленное технологическими факторами, фактические коэффициенты вариации прочности цементобетона на растяжение при изгибе, модуль упругости цементобетона, коэффициент постели грунта и искусственного основания, нарастание прочности цементобетона во времени;
эксплуатационные факторы: интенсивность и состав движения воздушных судов, статистические параметры, характеризующие вероятностный характер распределения нагрузок от колес главных опор по ширине отдельных участков аэродромных покрытий, статистические параметры и закономерность распределения взлетных масс однотипных воздушных судов, скорость движения и влияние подъемной силы крыла, динамичность воздействия нагрузок, усталостные явления в цементобетоне, накопление остаточных осадок в грунтовом основании и возможность эпизодической эксплуатации покрытия нагрузками, превышающими расчетную.
Математическая модель вероятностного расчета конструкции жесткого покрытия на стадии проектирования с заданным уровнем надежности может быть записана в следующей форме:
|
Р{arg Ф[F(mu) - F(md) - F(mt)] ≥ 0} = Рн = 1 - α |
(2) |
где Р - вероятность выполнения условия прочности жесткого аэродромного покрытия по первому предельному состоянию в течение заданного срока службы,
Рн - заданный уровень надежности;
Ф - интегральная функция распределения и резерва прочности покрытия; а - уровень риска заказчика;
F(mu) - интегральная функция распределения случайной величины предельного изгибающего момента, определяемая по формуле
|
|
|
|
(4) |
|
|
(5) |
где R28 - прочность цементобетона на растяжение при изгибе в возрасте 28 суток;
t - толщина плиты;
п - заданный срок службы покрытия;
u - число приложений нагрузок в расчетном сечении плиты;
F(md) – интегральная функция распределения случайной величины изгибающего момента в расчетном сечении плиты от воздействия колес главных опор воздушного судна, определяемая по формуле
|
|
(6) |
где φ(Fd, nгл, nk, xk, yk, t, Еb, Кs) - четырехмерная плотность вероятности распределения случайной величины изгибающего момента в плите от воздействия колес главной опоры;
Fd - нагрузка на колесо главной опоры шасси расчетного воздушного судна;
|
|
(7) |
M - среднее значение взлетной массы воздушного судна;
g - ускорение свободного падения;
kгл - коэффициент, учитывающий долю взлетной массы воздушного судна, приходящуюся на главные опоры;
kd и γt - соответственно коэффициенты динамичности и разгрузки, принимаемые по СНиП 2.05.08-85 /2/;
пгл и nk - соответственно число главных опор шасси и количество колес на главной опоре;
хk, yk - координаты колес главной опоры шасси;
Еb - модуль упругости цементобетона;
ks - коэффициент постели грунтового основания (или эквивалентный коэффициент постели слоистого основания);
F(mt) - интегральная функция распределения случайной величины изгибающего момента в краевой зоне на подошве плиты от воздействия температуры;
|
|
(8) |
ψ(а, t, E, A) - трехмерная плотность распределения случайной величины mt:
|
ψ(α, t, Е, А) = 0,437αt2ЕbА |
(9) |
где α - коэффициент линейного расширения цементобетона;
А - средняя амплитуда колебаний температуры цементобетона на поверхности плиты.
Входными параметрами предложенной модели подсистемы обеспечения надежности жестких покрытий на стадии проектирования являются: математическое ожидание, среднеквадратические отклонения, минимальные и максимальные значения случайных величин расчетного и предельного изгибающих моментов, а также интегральные функции их распределений Ф(md) и Ф(mu). Вероятность Р безотказной работы конкретной конструкции жесткого покрытия по первому предельному состоянию может быть найдена на основе решения уравнения (3) графоаналитическим методом как Р = 1 - α. Величина α при этом соответствует ординате точки пересечения интегральных кривых распределений расчетного изгибающего момента F(md) и предельного изгибающего момента F(mu) (см. рис.).
Полученное значение Р соответствует функциональной надежности принятой конструкции жесткого покрытия. Если найденная величина Р ниже заданного уровня надежности Рн, то необходимо рассмотреть альтернативные решения конструкций с последующей оценкой функциональной надежности, долговечности и приведенных затрат.
По завершению строительства функциональная надежность покрытия должна быть уточнена с использованием статистических параметров прочности и деформативности материалов, полученных по данным контроля качества производства работ и строительных материалов построечными лабораториями
В дальнейшем возможно уточнение разработанной модели подсистемы обеспечения надежности жестких покрытий на основе использования результатов оценки эксплуатационного состояния покрытий и накопленных данных, характеризующих вероятностно-статистические закономерности распределения входных переменных: нагрузок от воздушных судов (взлетных масс), характеристик конструкции покрытия и технологических факторов (прочности цементобетона на растяжение при изгибе, коэффициента постели грунта, толщины плиты), природно-климатических и эксплуатационных факторов (амплитуды колебаний температуры и солнечной радиации на поверхности покрытия, влажности грунта и числа приложений нагрузок от главных опор воздушных судов по ширине отдельных участков аэродромных покрытий).
Для реализации предложенной модели расчета функциональной надежности жесткого покрытия аэродромов может быть использован метод статистического моделирования Монте-Карло.
ЛИТЕРАТУРА
1. Тригони B.E. Основы автоматизированного проектирования аэродромов / МАДИ. - М., 1985 - 103 с.
2. СНиП 2.05.08-85 Аэродромы. - М.: ЦИТП Госстроя СССР, 1985.- 59 с
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Д-р. техн. наук, проф. Г.И. Глушков
ПОВЫШЕНИЕ НАУЧНО-ТЕХНИЧЕСКОГО УРОВНЯ ПРОЕКТИРОВАНИЯ ПОКРЫТИЙ АЭРОДРОМОВ
Развитие аэродромов существенно зависит от тенденции развития воздушных судов. Продолжающееся в настоящее время развитие авиации сохраняет имеющуюся тенденцию роста взлетной массы воздушных судов. Находящиеся в настоящее время в эксплуатации тяжелые транспортные самолеты имеют взлетную массу 160 - 320 т. Проектируются и ожидаются в ближайшей перспективе самолеты со взлетной массой 400 - 600 т. Рассматриваются проекты самолетов со взлетным весом 1000 т. Так, проектируемый фирмой «Локхид» (США) вариант грузового самолета имеет взлетную массу 2000 т.
Рост взлетного веса и
интенсивности движения самолетов привел к необходимости увеличивать общую
толщину аэродромных покрытий. Расчетная толщина аэродромных покрытий нередко
стала достигать 80 -
Основные результаты этих исследований, их обобщение и анализ рассмотрены ниже. Их использование в практике проектирования аэродромов позволит повысить надежность работы покрытий, уменьшить их материалоемкость и стоимость
Расчетные нагрузки
С целью оценки
правильности существующего зонирования аэродромных покрытий на группы участков
и выявления закономерности распределения нагрузок от современных самолетов Ил-
Запишем проекции всех сил на оси ОХ и OY.
|
|
(1) |
![]() = 0. N - (G cos γ - Y) = 0,
= 0. N - (G cos γ - Y) = 0,
где М - масса самолета;
G - вес самолета;
V - скорость движения самолета;
X - сила лобового сопротивления самолета;
Y- аэродинамическая подъемная сила;
F - силы трения колес самолета о поверхность ИВПП;
R0 - тяга двигателя самолета;
Из уравнений (1) найдем выражение нагрузки от колес главных опор самолета на покрытие ИВПП:
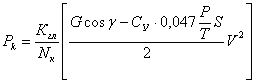
где СУ - коэффициент аэродинамической подъемной силы;
S - площадь крыла самолета;
Кгл - доля веса самолета, приходящегося на главные опоры;
V - скорость движения самолета;
Nк - количество колес на главной опоре.
Использование полученной формулы позволило определить вертикальные нагрузки от современных самолетов по длине ИВПП и вычислить коэффициент разгрузки.
Анализ выполненных расчетов показывает на значительное уменьшение коэффициента разгрузки для современных самолетов, по сравнению с коэффициентами разгрузки, принятыми в настоящее время по СНиП II-85 «Аэродромы», что свидетельствует о возможности уменьшения толщины покрытий по длине ИВПП.
Учет краевого загружения при расчете плит жестких покрытий аэродромов на прочность
При расчете аэродромных покрытий по существующей методике (см. СНиП 2.05.08-85) краевое загружение учитывается увеличением центрального изгибающего момента на соответствующий переходной коэффициент К. Для бетонных и армобетонных покрытий при наличии стыковых соединительных швов покрытий К =1,2; при сквозных швах К = 1,5.
Принятые значения переходных коэффициентов не учитывают схему шасси самолетных нагрузок (количество полос, давление в шинах). Для устранения отмеченных недостатков было получено новое решение на основе метода конечных элементов и метода компенсирующих нагрузок.
По методу компенсирующих нагрузок принцип расчета состоит из двух этапов.
Основное решение получено дополнением полубесконечной плиты до бесконечной. Для нее определяют изгибающие моменты от заданной и отраженной силы по формулам.
Нагрузка, равномерно распределенная на площади круга, радиусом а, определяется по формуле:
при ξ < а
|
|
(2) |
при ξ > а
|
|
(2а) |
где Gp - изгибающие моменты;
ξ - приведенное расстояние от центра круга до рассматриваемой точки;
g0 - нагрузка на площадку;
![]() = приведенный радиус круга;
= приведенный радиус круга;
r - радиус круга;
l - упругая характеристика плиты;
gQ(α)VQ(α)f(α) - расчетные функции в методе компенсирующих нагрузок.
Компенсирующее решение. Изгибающие моменты определяем по формулам
|
|
(3) |
|
|
(3а) |
где ![]() ,
, ![]() - единичные значения моментов,
принимаемые в зависимости от расстояния до края плиты по методу компенсирующих
нагрузок.
- единичные значения моментов,
принимаемые в зависимости от расстояния до края плиты по методу компенсирующих
нагрузок.
Результаты расчетов для самолетов Ил-86 и ТУ-154 приведены в таблице.
Таблица
|
Вид самолета |
Приведенное расстояние |
Переходный коэффициент для свободного края |
Переходный коэффициент для стыкового соединения |
|
Ил-86 |
0,26 |
1,53 |
1,0 |
|
0,40 |
1,33 |
0,87 |
|
|
0,50 |
1,23 |
0,79 |
|
|
0,60 |
1,00 |
0,65 |
|
|
Ту-154 |
0,40 |
1,78 |
1,15 |
|
1,00 |
1,38 |
0,89 |
|
|
1,20 |
1,17 |
0,63 |
|
|
0,20 |
1,03 |
0,64 |
Анализ данных таблицы свидетельствует о том, что величины изгибающих моментов для краевого загружения на 5 - 12 % ниже по сравнению с расчетными значениями, определенными по СНиП II-47-85 «Аэродромы». Применение изложенной методики позволяет снизить потребную толщину покрытий аэродромов и обеспечить экономический эффект.
Проектирование аэродромных покрытий с учетом деформации поперечного сдвига
При расчете жестких покрытий в настоящее время учитывают только нормальные напряжения. В ряде случаев определение расчетных изгибающих моментов целесообразно и с учетом касательных напряжений.
Расчет покрытий с учетом касательных напряжений (деформаций сдвига) основывается на решении следующего дифференциального уравнения:
|
|
(4) |
где ψ - функция напряжений.
Решение приведенного дифференциального уравнения дает возможность определять расчетные изгибающие моменты в покрытиях аэродромов:
![]() .
.
Значение коэффициента сдвига в зависимости от жесткости покрытия изменяется от 0,8 до 0,50, что существенно снижает момент, определяемый по СНиП II-47-85.
Расчет аэродромных покрытий с учетом касательных напряжений между слоями
В настоящее время при расчете жестких аэродромных покрытий касательные напряжения между отдельными слоями не учитываются. В основу учета касательных напряжений положена экспериментальная зависимость
|
T = k·U |
(5) |
где
k - модуль трения;
U - перемещение слоя.
Для учета касательных напряжений необходимо рассмотреть дифференциальное уравнение изгиба плиты с учетом касательных напряжений:
|
|
(6) |
где Nx, Ny - продольные силы, направленные по осям X и Y;
w - прогиб покрытия;
D - цилиндрическая жесткость плиты;
х, у - координаты точек;
С - коэффициент постели.
Решение полученного дифференциального уравнения показало, что значения расчетных моментов уменьшаются на 15 - 20 %.
Анализ выполненных исследований позволяет сделать следующие выводы:
1. Существующий метод расчета аэродромных покрытий жесткого типа не полностью учитывает их работу под действием современных самолетов.
2. Проектирование аэродромных покрытий целесообразно проводить с учетом расчетных нагрузок от современных самолетов; деформаций поперечного сдвига, краевого загружения от реальных главных опор (схемы расположения колес, количества полос, давления в шинах); касательных напряжений между слоями.
3. Учет результатов проведенных исследований позволяет снизить потребную толщину жестких аэродромных покрытий на 20 - 25 %.
ЛИТЕРАТУРА
1. Глушков Г.И. Расчет сооружений, заглубленных в грунт. - М.:
2. Нгуен Ван Льен. Расчет жестких покрытий с учетом трения // Проектирование аэродромов и эксплуатационная оценка прочности сооружений. Сб. научных трудов / МАДИ, 1985. - С. 34-41.
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Д-р. техн. наук, проф. Г.И. Глушков,
канд. техн. наук, ст. науч. сотр. С.В. Картошина
К РЕШЕНИЮ ЗАДАЧИ ИЗГИБА БЕСКОНЕЧНОЙ ПЛИТЫ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ, ЛЕЖАЩЕЙ НА АНИЗОТРОПНОМ ОСНОВАНИИ
По существующей методике расчета жестких покрытий грунтовое основание рассматривается как изотропное упругое тело, описываемое различными моделями. Модели эти характеризуются функцией влияния или, по терминологии Б.Г. Коренева [1], ядром основания, выражающим прогиб поверхности основания в точке X, Y при действии одиночной силы, приложенной в той же точке. Однако проведенные в последние годы эксперименты показали, что ряд грунтов имеют различные модули упругости в горизонтальной и вертикальной плоскостях. В этом случае, как следует из [2], функция ядра основания имеет вид аналогичной модели упругого изотропного полупространства, но с другой константой:
|
|
(1) |
здесь r - расстояние между точкой приложения силы и точкой, в которой рассматривается прогиб;
KT - постоянная, зависящая от упругих характеристик грунта,
|
|
(2) |
Входящая в (2) величина выражается следующим образом:
|
|
(3) |
В этих выражениях v0 и vz - коэффициенты Пуассона, характеризующие сжатие в горизонтальной и вертикальной плоскостях.
Для решения конкретных задач потребуется в дальнейшем функция с(λ), являющаяся преобразованием функции Ханкеля К(r). Определяя с(λ), получим
|
|
(4) |
При использовании прямоугольных координат
|
|
(5) |
Полученные значения функции с(λ) возможно использовать при решении конкретных задач в прямоугольных координатах. Например, прогиб бесконечной плиты w(x,y) при действии на нее произвольной нагрузки q(х,у) может быть определен из решения дифференциально-интегральной системы
|
|
(6) |
Здесь D - цилиндрическая жесткость плиты;
p(x,y) - функция контактных напряжений;
K(|u|,|v|) - ядро основания - функция, выражающая прогиб основания в точке X, Y при действии единичной силы, приложенной в точке ξ, η.
Введем вспомогательную величину
|
|
(7) |
и перейдем к новым координатам и функциям х = х1·h, у = у1·h,
|
|
(8) |
С учетом (8) система (6) примет вид:
|
|
(9) |
В дальнейшем для упрощения опустим индекс "1". При действии на плиту произвольной нагрузки q(х,у) ее можно представить в виде симметричной и кососимметричной составляющих. Для симметричной составляющей нагрузки при решении дифференциально-интегральной системы (9) используем двумерное косинус-преобразование функций Фурье w(x,y), p(x,y), К, q(x,y).
|
|
(10) |
Тогда из (9) получим выражение для прогибов плиты:
|
|
(11) |
В формулу (11) входит функция Q(ξ,η), являющаяся трансформантой функции Фурье, приложенной к плите нагрузки. Если к бесконечной плите приложена сосредоточенная сила в центре плиты, то
|
|
(12) |
При приложении в центре плиты равномерно распределенной нагрузки на площадке с размерами 2а×2в
|
|
(13) |
Подставив (12) или (13) в формулу (11), можно определить прогибы в бесконечной плите, находящейся на основании с различными модулями упругости в горизонтальной и вертикальной плоскостях.
ЛИТЕРАТУРА
1. Коренев Б.Г. Вопросы расчета балок и плит на упругом основании. - М.: Стройиздат, 1954. - 181 с.
2. Глушков Г.И. Расчет сооружений, заглубленных в грунт. - М.: Стройиздат, 1977. - 294 с.
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Канд. техн. наук А.И. Юрченко
УСЛОВИЯ ДОЛГОВЕЧНОСТИ И ТРЕБОВАНИЯ К ПРОЧНОСТИ АСФАЛЬТОБЕТОННЫХ ПОКРЫТИЙ И СЛОЕВ УСИЛЕНИЯ
Существующие методы расчета и конструирования асфальтобетонных покрытий не учитывают возможность образования на них температурных трещин и сдвигов. Между тем вопрос предотвращения образования температурных трещин и сдвигов продолжает оставаться чрезвычайно актуальным.
Оценка долговечности работы слоев усиления усложнена по сравнению с оценкой этого показателя собственно для асфальтобетона тем, что здесь следует учитывать надежность совместной работы слоя усиления с усиливаемым покрытием, стабильность работы слоев искусственных и естественного оснований, работы всего пакета слоев дорожной и аэродромной одежды.
Ни действующий ГОСТ на асфальтобетон дорожный, ни один из применяемых методов расчета асфальтобетонных покрытий не учитывают возможность образования сдвиговых и температурных деформаций (в пределах годового цикла) в покрытии.
Долговечность асфальтобетонных слоев усиления, наряду с отмеченными выше факторами, во многом определяется наличием и развитием так называемых «отраженных» трещин, возникающих над трещинами усиливаемого покрытия. Генезис «отраженных» трещин обусловлен влиянием температурно-влажностных изменений при взаимодействии слоя усиления с усиливаемым покрытием, а также эксплуатационными воздействиями транспортных средств, приводящих к неравномерному деформированию слоев усиления и существующего покрытия (одежды). Стабильность работы слоя усиления во многом определяется надежностью его сцепления с нижележащим слоем.
Известно, что асфальтобетон резко меняет свои свойства от температуры: при положительной температуре он обладает свойствами вязкопластичного материала, при отрицательной - упругого. Изменение температуры резко влияет на деформативные и прочностные свойства асфальтобетона. Так, в летнее время температура воздуха в ряде дорожно-климатических зон (III - V) достигает 40 - 50°С, За счет солнечной инсоляции тепла поверхность асфальтобетонных покрытий даже во II ДКЗ может нагреваться до 60 - 70°С, а в южных районах страны - до 80 - 90°С. В этих условиях битум может начать плавиться, а асфальтобетон сильно размягчаться на разной глубине и накапливать пластические деформации. В покрытиях возникают колейность и другие сдвиговые деформации. И, наоборот, при отрицательных температурах асфальтобетон становится упругим и хрупким, что может привести к образованию трещин, уже в первые же осенне-зимние морозы.
Характерной особенностью по обеспечению долговечности асфальтобетонных покрытий в этих условиях является необходимость учета в расчетной модели поведения асфальтобетона реологической и механической моделей. Наиболее приемлемой для этих целей является совмещенная реологическая модель, предложенная проф. А.М. Богуславским [1, 2], учитывающая упруговязкопластические свойства асфальтобетона в широком температурном интервале. В этой совмещенной модели к модели Кельвина и Максвелла добавлена модель Сен-Венана, что позволяет учитывать пластичность асфальтобетона с целью обеспечения его сдвигоустойчивости. Методика расчета по обеспечению долговечности асфальтобетонных покрытий с учетом реологических параметров должна предусматривать два расчетных случая:
1) работа покрытий в летний период при высоких температурах, когда проявляются сдвиговые деформации от возникновения горизонтальных сил при движении транспортных средств;
2) работа асфальтобетонных покрытий при низкой температуре (ее критические перепады могут привести к разрывам и разрушению покрытий в осенне-зимний период).
В первом случае требуемую прочность асфальтобетона на сжатие (R50) можно определить по формуле
|
|
(1) |
где РК - удельное давление от колеса транспортного средства;
τР(+) - продолжительность срока службы покрытия при высокой расчетной температуре;
θ - время релаксации;
τ - время ретардации;
а - опытный коэффициент равный 0,15;
Р1 и Р2 - показатели, характеризующие кинетику деформации асфальтобетона.
Параметры асфальтобетона θ, τ, Р1, Р2, а могут быть установлены по опубликованным данным или по результатам лабораторных испытаний образцов.
Во втором случае требуемая прочность асфальтобетонных покрытий при отрицательных температурах (R-10) может быть вычислена по формуле
|
|
(2) |
где σ - температурные напряжения (расчетные значения);
τР(-) - продолжительность нахождения асфальтобетона в напряженном состоянии, зависящая от скорости охлаждения; при V1 = 10 град./ч. - 360 с, при V2 = 1 град./ч - 360 с;
а - эмпирический коэффициент, равный 4.
Температурные напряжения σ определяются по формуле
|
|
(3) |
где α - α0 - разность коэффициентов температурного расширения асфальтобетона и основания;
t2 - t1 - разность температур (перепад);
V1 - скорость охлаждения, наблюдаемая в данной местности;
V0 - равновесная скорость охлаждения (0,4 град./ч);
E - модуль упругости.
Расчеты по формулам (2) и (3) показывают, что напряжения сжатия, возникающие в асфальтобетонных слоях в результате быстрого охлаждения могут быть выше или ниже фактической прочности асфальтобетона. Если эти напряжения сжатия ниже фактической прочности, то разрушение покрытия в результате температурных напряжений не произойдет. Поэтому требуемая прочность асфальтобетонных покрытий или слоев усиления должна быть равна или выше возникающих в них температурных напряжений.
На долговечность материалов с коагуляционной структурой, к которым относятся асфальтобетоны, большое влияние оказывает фактор времени - длительность воздействия нагрузок при положительных и отрицательных температурах. Зависимость напряжений и деформаций, возникающих в асфальтобетоне при нагружении, от времени действия нагрузки обусловлена его вязкими и пластичными свойствами. Под действием нагрузок в асфальтобетоне могут происходить релаксационные и ретардационные процессы.
Одним из методов исследования реологических свойств асфальтобетонов является испытание его на ползучесть под действием постоянных нагрузок [1]. Испытания проводятся на образцах-балочках 4×4×16 см при нагрузке 0,2 0,25 и 0,3 от разрушающей нагрузки. По результатам испытаний стоят график зависимости деформации от времени действия нагрузки. В логарифмических координатах график этой зависимости обращается в прямую линию, наклон которой в абсциссе графика определяет степень пластичности асфальтобетона. Показателем деформативной способности асфальтобетона, отражающим реологические свойства этого материала, является вязкость его ненарушенной структуры, рассчитываемая по результатам испытаний образцов-балочек:
|
|
(4) |
где Р - нагрузка (0,2 - 0,3 от разрушающей нагрузки), кг;
l, b, h - длина, ширина, высота балочки, см;
v - скорость вязкого прогиба середины балочки (тангенс угла наклона прямолинейного участка кривой ползучести к оси времени), мм/мин.
Прогнозирование
долговечности асфальтобетона в слое дорожного покрытия возможно, если известны
такие реологические параметры материала, как время релаксации θ,
время ретардации τ, коэффициент вязкости по
Максвеллу ηм, модуль упругости Ес,
кинетические характеристики Р1, Р2 и ![]() . Данные реологические параметры определяются расчетом по
результатам испытаний сжатием на гидравлическом прессе цилиндрических образцов,
сформированных из асфальтобетонных смесей под нагрузкой 40 МПа при времени ее
действия 3 мин, при температурах образцов от -10 до +50°С.
. Данные реологические параметры определяются расчетом по
результатам испытаний сжатием на гидравлическом прессе цилиндрических образцов,
сформированных из асфальтобетонных смесей под нагрузкой 40 МПа при времени ее
действия 3 мин, при температурах образцов от -10 до +50°С.
Реологические параметры определяют по формулам:
время релаксации
|
|
(5) |
время ретардации
|
|
(6) |
модуль упругости
|
|
(7) |
коэффициент вязкости по Максвеллу
|
ηМ = θ·ЕС |
(8) |
коэффициент вязкой податливости
|
|
(9) |
кинетические характеристики
|
|
(10) |
где h и d - высота и диаметр образца до испытания, см;
Δh и dΔ - деформации сжатия и расширения образца при испытаний, см.
Деформативные свойства
асфальтобетона отражает показатель ![]() , являющийся отношением характеристики скорости уменьшения сопротивляемости
деформированию к характеристике скорости роста упругой деформации в материале.
Для обеспечения деформационной устойчивости асфальтобетона при высоких
положительных температурах (+50°С) этот показатель не должен превышать 0,005, а
при отрицательных температурах (-10°С) он должен быть не менее 0,0003 [1].
, являющийся отношением характеристики скорости уменьшения сопротивляемости
деформированию к характеристике скорости роста упругой деформации в материале.
Для обеспечения деформационной устойчивости асфальтобетона при высоких
положительных температурах (+50°С) этот показатель не должен превышать 0,005, а
при отрицательных температурах (-10°С) он должен быть не менее 0,0003 [1].
Для летнего периода из условия длительности работы материала при температуре +50°С характеристика его долговечности может быть определена по формуле
|
|
(11) |
где а - коэффициент, равный 0,25 (в диапазоне t = + 50 ÷ +20°С);
ρ - уровень
напряжений (![]() ); где: σ - величина
напряжения (приведенное удельное давление от колеса);
); где: σ - величина
напряжения (приведенное удельное давление от колеса);
τР(t) - заданный срок службы покрытия (слоя усиления).
Требуемую долговечность асфальтобетонного покрытия при высоких положительных температурах в летний период определяют по формуле
|
|
(12) |
где Т1 - заданное количество лет (опасный срок: Т1 = 5);
Т2 - количество дней в году, в которые температура покрытия выше +50°С; (Т2 = 28 для Московской области);
Т3 - количество часов в день, в которые температура покрытия равна +50°С; (Т3 = 3 для Московской области);
ti - продолжительность единичного нагружения (ti = 0,1 с у мест остановки, ti = 0,001 с. на перегоне);
п - интенсивность движения расчетных транспортных средств (при суточной интенсивности 2000 транспортных средств на одной полосе в сутки п = 100 ед./ч), ед./ч
Прочность
асфальтобетона в расчете на сдвигоустойчивость может быть установлена из
условия ![]() =
= ![]() при заданных
расчетных значениях долговечности и действующих напряжениях:
при заданных
расчетных значениях долговечности и действующих напряжениях:
|
|
(13) |
Одной из причин снижения долговечности дорожных и аэродромных асфальтобетонных покрытий является нарушение их ровности за счет пластической компоненты деформации εzn, которое может возникать при малой сдвигоустойчивости асфальтобетона в слое покрытия. Ровность покрытия обеспечивается, если в течение заданного срока его службы (опасный период) величина εzn для асфальтобетона не превышает 0,0016 [1]. При этом расчетное значение εzn определяется по уравнению
|
|
(14) |
Снижение деформативной способности асфальтобетона имеет место при отрицательных температурах в зимний период в результате образования в нем полидисперсных органических кристаллов и структурных модификаций Температурные напряжения и деформации, возникающие в асфальтобетоне в зимний период при воздействии отрицательных температурах и неравномерном поднятии земляного полотна, могут привести к образованию трещин в слое покрытия и снижению срока его службы.
Долговечность асфальтобетона при низких температурах может быть найдена по следующей формуле:
|
|
(15) |
где а - эмпирический коэффициент, равный 4;
ρ - уровень напряженности.
ЛИТЕРАТУРА
1. Богуславский А.М. Богуславский Л.А. Основы реологии асфальтобетона - М.: Высшая школа, 1972. - 200 с.
2. Дорожный асфальтобетон / Под ред. Л.Б. Гезенцвея. - М.: Транспорт, 1985. - 196 с.-32-
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Инженер Л.Ю. Артемова
К ВОПРОСУ НЕПОЛНОГО КОНТАКТА ПЛИТЫ С ОСНОВАНИЕМ
Появление на авиалиниях в
ближайшем будущем воздушных судов с полезным весом 300 - 400 т и посадочной
скоростью порядка
Вместе с тем анализ состояния аэродромных покрытий, проведенный ведущим в этой области институтом «Аэропроект», показал, что срок их службы, как правило, меньше нормативного и что они начинают разрушаться через 2 - 3 года после ввода в эксплуатацию [1]. В этом же анализе приводится ряд причин, снижающих долговечность покрытий. Наиболее характерными из них являются: недоучет природно-климатических, грунтово-геологических, гидравлических, мерзлотных условий строительства; ошибки при разработке аэродромной конструкции и ее расчете; нарушение технологии строительства покрытий и несоблюдение правил их эксплуатационного содержания. Исходя из этого можно отметить, что вопросы расчета и проектирования аэродромных покрытий решены не в полной мере и требуют дальнейшего совершенствования.
Опыт эксплуатации жестких дорожно-аэродромных покрытий показывает, что между плитой покрытия и основанием возможно образование местных зазоров, величина и область распространения которых неодинакова в различных зонах под плитой [2 - 11]. Большинство исследователей отмечают, что нарушение контакта плиты с основанием происходит в результате многократного воздействия на покрытие колес автомобилей или самолетов, изменения внешних температурных условий, нарушения водного режима и технологии возведения основания.
При многократном
воздействии подвижных нагрузок происходит накопление остаточных просадок грунта
подстилающего покрытия. При этом плиты покрытия в отдельных местах перестают
опираться на грунт и начинают работать как консольные балки. Несущая
способность плит в этом случае снижается, а ее прогибы увеличиваются. Так, в
работе [3]
показано, что наличие под плитой жесткого покрытия зазора в
Интересные результаты опытных исследований [6] показывают, что при наличии зазора плита сборного аэродромного покрытия может работать как консольная или однопролетная балка. Загружение консоли вызывает увеличение изгибающих моментов по сравнению с изгибающими моментами при плотном контакте в 1,2 - 1,55 раза, а при расположении нагрузки в середине пролета значения изгибающих моментов возрастают в 1,25 - 1,65 раза. В результате этих испытаний также установлено, что плита в напряженном состоянии, опирающаяся на основание с пониженным коэффициентом постели, оказывается в более благоприятных условиях, чем плита на основании, характеризуемом высоким коэффициентом постели.
Известно, что коробление
плиты, вызываемое неравномерностью температуры плиты по ее толщине, также может
привести к отрыву плиты от основания. Опытные результаты [2] подтверждают, что
при температурном короблении возможен отрыв от основания либо средней части
плиты, либо ее контурных участков. При этом величина зазора между плитой и
основанием достигает
Различные по назначению швы в жестких покрытиях являются очагами разрушения не только покрытия, но и его основания [4, 7].
При эксплуатации покрытия вода через швы может попадать в его основание. Под действием колесной нагрузки плита, начиная колебаться, вызывает в зонах скопления воды ее пульсацию. В результате движения воды происходят размывание и вынос материала основания (особенно под краями плит) и, как следствие, образование пустот под плитами. Такое ухудшение схемы работы плит приводит к их перенапряжению.
Для сборных жестких покрытий, несмотря на применение различного вида выравнивающих слоев и способов посадки плит, неполное опирание плит практически неизбежно. С учетом этого в нормативных документах [12, 13] предусмотрено, что требуемая площадь контакта должна составлять не менее 95 % от общей площади плиты.
В теоретическом плане учет неполного контакта плиты с основанием представляет собой сложную задачу. Однако такие решения с определенной степенью точности для выбранных расчетных схем и краевых условий имеются.
Так, в работе [5] рассматривается полубесконечная балочная плита на упругом винклеровском основании. Расчетная схема представляет собой равномерно чередующиеся контактные и бесконтактные участки, а учет начального зазора производится введением в шестичленные уравнения фиктивных нагрузок. Решение уравнений осуществляется смешанным методом строительной механики.
Авторы [10] рассматривают изгиб бесконечной ортотропной плиты при действии сосредоточенной нагрузки и собственного веса плиты с учетом зазора между плитой и основанием, вызванного многократным приложением нагрузки. Задача сводится к определению прогибов плиты ограниченных размеров и решается методом локальных вариаций. Полученные результаты свидетельствуют о том, что наличие зазора вызывает в плите дополнительный изгибающий момент, составляющий 10 - 15 % от величины момента, возникающего в плите, полностью опертой на упругое основание.
В работе [11] предлагается система канонических уравнений для решения шестиугольной в плане плиты, лежащей на основании, допускающем образование остаточных деформаций. Из графических результатов расчета при конкретных значениях нагрузок и коэффициентов постели видно, что остаточные деформации основания способствуют увеличению изгибающего момента в центре плиты от 40 до 70 %.
Вопросу расчета плиты с учетом остаточных деформаций основания при действии многократно повторяющихся нагрузок посвящена статья [9], в которой приведены решения, показывающие, что остаточные прогибы покрытия зависят от механических свойств грунтового основания.
Многочисленные исследования привели к тому, что в нормативный документ [14] был введен коэффициент, учитывающий накопление остаточных прогибов в основании, равный 1 – 1,1.
Для количественной оценки напряженного состояния плиты, имеющей неполный контакт с основанием, был выполнен тестовый пример расчета такой плиты, который также подтверждает значимость этой задачи.
В качестве расчетной
модели была принята аэродромная плита марки ПАГ-14 длиной
Основание плиты принято в
виде модели упругого полупространства с модулем деформации Е = 600 кг/см2
и μ = 0,1. Нагрузка приложена в
центре плиты в виде сосредоточенной силы F =
Рассмотрено два варианта: первый (рис. а) - плита имеет полный контакт с основанием; второй (рис. б) - между плитой и основанием существует зазор размером 40×30 см (площадь зазора 1200 см2, т.е. 1 % от общей площади плиты).
Расчет произведен методом конечных элементов; размер элемента принят 20×15 см. Результаты расчета для точек 1, 2 (рис.) сведены в табл.
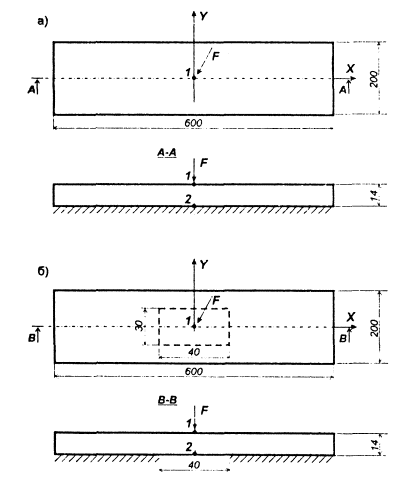
Рис. Расчетная схема плиты без зазора (а) и с зазором (б) (размеры в см)
Таблица
|
№ варианта |
Прогиб в точке |
Напряжение (кг/см2) в точке |
Примечание |
|||
|
1 |
2 |
|||||
|
ось X |
ось У |
ось X |
ось У |
|||
|
1 |
0,0752 100 % |
-6,652 100 % |
-7,095 100 % |
5,009 100 % |
5335 100 % |
- сжатие, + растяжение |
|
2 |
0,0865 115 % |
-7,383 111 % |
-7,626 107,5 % |
5,730 114 % |
5,867 110 % |
|
Анализ результатов (табл.) показывает, что наличие даже незначительного по площади зазора между покрытием и основанием существенно изменяет напряженно-деформированное состояние плиты покрытия. Например, прогибы увеличиваются на 15 %, а напряжения возрастают от 7,5 до 14 %.
На основании изложенного можно сделать следующие выводы.
1. Многолетние наблюдения за состоянием дорожно-аэродромных покрытий жесткого типа подтверждают, что они могут работать в условиях неполного контакта с основанием. Краткий анализ литературных данных позволил установить основные причины возникновения «зависания» плит. Это многократность приложения внешней нагрузки; температурные коробления плиты; изменение водного режима основания; нарушение технологии изготовления основания (для сборных покрытий).
2. Существующие теоретические методы учета начального зазора между плитой покрытия и основанием говорят о важности этого вопроса и сложности его решения. Имеющиеся результаты противоречивы и не подтверждены опытными данными.
3. Результаты тестового расчета подтверждают, что наличие зазора между жестким покрытием и основанием ухудшает напряженно-деформированное состояние плиты покрытия. Так, согласно проведенному расчету напряжения могут возрасти до 14 %, а прогиб до 15 %.
4. Наличие неполного контакта плиты с основанием влияет на напряженно-деформированное состояние как самой плиты, так и ее основания и требует дальнейших исследований этой проблемы, основными задачами которых являются:
- выбор модели «плита - основание» и ее обоснование с учетом реального расположения нагрузок, климатических воздействий, конструктивных особенностей жестких покрытий и физико-механических свойств основания и материала плиты;
- теоретическая и экспериментальная оценка напряженного состояния плиты с учетом наличия зазора под плитой;
- определение или уточнение значений существующих коэффициентов, учитывающих неполный контакт плиты с основанием.
ЛИТЕРАТУРА
1. Иванов В.Н. Аэропроект и аэропорты - М.: Воздушный транспорт, 1998. - 262 с.
2. Левицкий Е.Ф., Чернигов В.А. Бетонные покрытия автомобильных дорог. - М.: Транспорт, 1980. - 288 с.
3. Глушков Г.И., Бабков В.Ф., Тригони В.Е. и др. Жесткие покрытия аэродромов и автомобильных дорог. - М.: Транспорт, 1994. - 350 с.
4. Гордон К. Рей. 35 лет развития бетонных дорожных покрытий. / Пер. с испан. - Минск, 1982. - 27 с.
5. Демин В.И. К расчету балочных плит на упругом основании с учетом начального зазора. Тр. ГОСНИИ гражданской авиации. Вып. 9, 1981.- С. 9-11.
6. Пчелкина Л.В., Демин В.И., Кульчицкий В.А. Влияние начальных зазоров на напряженное состояние сборного покрытия. Автомобильные дороги. № 3, 1986. - С. 18-19.
7. Соколов А.Н. Применение дренирующих слоев в основании сборного аэродромного покрытия. Автомобильные дороги. № 12, 1990. - С. 14-16.
8. Васильев Н.В., Демин В.И. Устройство стыковых соединений в сборных покрытиях. Автомобильные дороги. № 12, 1985. - С. 8-9
9. Глушков Г.И. Расчет аэродромных покрытий с учетом остаточных деформаций основания. Труды МАДИ. Вып. 57, 1973. - С. 25-33.
10. Медников И.А., Матвеев С.А. Расчет ортотропной плиты при неполном контакте с упругим основанием / Труды МАДИ, 1981. - С. 34-45.
11. Янин А.Е. Жесткие покрытия сельскохозяйственных аэродромов и подъездных путей: Автореф. канд. дис - М., 1991. -19 с.
12. СНиП 3.06.03-85. Автомобильные дороги. - М.: Стройиздат, 1986. -100 с.
13. СНиП III-46-79. Аэродромы. Правила производства и приемки работ. - М.: Стройиздат, 1981. -113 с.
14. СНиП 2.05.08-85. Аэродромы. - М.: Стройиздат, 1985. - 59 с.-40-
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Д-р техн. наук, проф. Г.И. Попов,
инженер Г.И. Филимошкина
СПОСОБ РАСЧЕТА НЕСУЩЕЙ СПОСОБНОСТИ ИЗГИБАЕМЫХ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ
Нам неизвестны способы расчета прочности изгибаемых железобетонных элементов, которые одновременно учитывали бы влияние масштабного фактора и класса прочности бетона на форму эпюры напряжений сжатой зоны, прочностные и деформационные показатели \ сжатого бетона. В одной из последних публикаций [1] ставится вопрос о необходимости разработки дополнительной главы СНиП по расчету крупноразмерных железобетонных конструкций. Не менее актуально этот вопрос стоит и в отношении малоразмерных железобетонных элементов, а точнее - элементов, у которых высота сжатой зоны мала.
Ниже излагается инженерный способ расчета прочности изгибаемых железобетонных элементов, учитывающий влияние их размеров и прочности бетона на характер его механических свойств в сжатой зоне. Представлено два расчета, упрощенный вариант и уточненный вариант, - а также показывается связь между ними. Способ основан на результатах экспериментальных исследований, проведенных Г.И. Филимошкиной в 80-е гг. [6]. Некоторые новые результаты изложены в [6].
Упрощенный вариант
Принимается прямоугольная эпюра напряжений в сжатом бетоне с укороченной высотой сжатой зоны х и приведенной прочностью на сжатие при изгибе, однако прочность на сжатие при изгибе Rи.прив = f(х) ставится в зависимость от высоты х.
Так как для экспериментальной кривой Rи.прив = f(х) нe может быть подобрана (с удовлетворительным приближением) степенная функция 2й и 3й степени, принимаем эту зависимость в виде кусочно-линейного многочлена (рис. 1). Структура формул для отрезков х ≤ хизл1, хизл1 ≤ х ≤ хизл2 меняется, поэтому индексацию величин в формулах упрощаем. Уравнение равновесия проекций внутренних сил (рис.2) имеет вид
|
Rи.прив(x)·b·x = Rs·As |
(1) |
где
|
Rи.прив(x) = Rи.прив.0 - kR·x |
(2) |
|
|
(3) |
Величины Rи.прив.0 и х0 разные (см. рис. 1) для х ≤ хизл.1, и хизл.1 ≤ х ≤ хизл.2 зависят также от класса прочности бетона на сжатие.
Вводя безразмерные коэффициенты
|
|
(4) |
вместо (1) получим
|
|
(5) |
При η0 → ∞ (Rи.прив.х не зависит от х) ξ = aR,0 придем к обычной формуле ξ = aR,0 (относительная высота сжатой зоны равна относительной силе армирования). Из (5) определяется относительная высота сжатой зоны
|
|
(6) |
Уравнение равновесия моментов внешних и внутренних сил относительно оси растянутой арматуры имеет вид
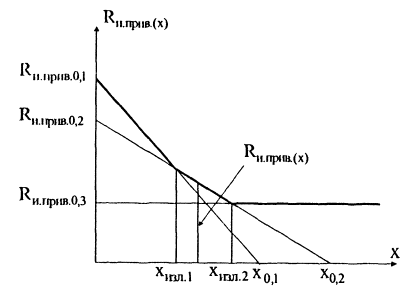
Рис. 1. Расчетная зависимость Rи.прив(x) от высоты сжатой зоны
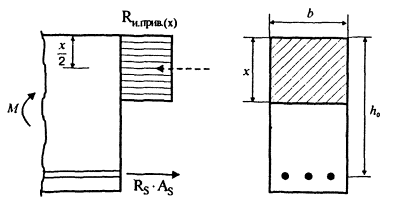
Рис. 2. Схема внутренних и внешних усилий в нормальном сечении
|
М = Rи.прив.(х)·b·x·(ho - x/2) |
(7) |
или с учетом (2), (3), (4)
|
М = Rи.прив.(0)·b· |
(8) |
где
|
|
(9) |
Для ξ, А0, γ0,
i0, γ0
= (1 - 0,55ξ), 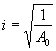 могут быть составлены
вспомогательные таблицы, делающие практические работы элементарными.
могут быть составлены
вспомогательные таблицы, делающие практические работы элементарными.
Уточненный вариант
Уточняется зависимость σ = f(εb)
На диаграмме σb - εb (рис. 3) можно выделить четыре узловых точки: ![]() ,
, ![]() , Rи.эксп, σbC.
Напрашивается применение 4-звенной сплайн-функции [7]. Однако, если приближать
кусочно-линейный многочлен к экспериментальной кривой по Чебышеву или в
среднем, достаточно трехзвенной ломаной линии. Такое приближение гораздо точнее
линейного сплайна и не уступает по точности квадратному и кубическому сплайнам,
будучи несоизмеримым с ними по трудоемкости практических расчетов.
, Rи.эксп, σbC.
Напрашивается применение 4-звенной сплайн-функции [7]. Однако, если приближать
кусочно-линейный многочлен к экспериментальной кривой по Чебышеву или в
среднем, достаточно трехзвенной ломаной линии. Такое приближение гораздо точнее
линейного сплайна и не уступает по точности квадратному и кубическому сплайнам,
будучи несоизмеримым с ними по трудоемкости практических расчетов.
* Попов Г.И попросил доктора физ.-мат. наук, проф. М.Н. Олевского решить задачу о
наилучшем приближении кусочно-линейного многочлена к гладкой кривой. М.Н.
Олевский решил эту задачу в
* Профессору С.П. Тимошенко удалось найти точное значение частоты свободных колебаний нелинейной системы с одной степенью свободы, пружина которой сопротивляется перемещению массы по закону кубической параболы. При замене параболы двухзвенной ломаной ошибка составила [4]: при приближении по Чебышеву - 0,28 %, при приближении в среднем - 5,52 %.
При замене полукруга (1-я производная дуги окружности меняется от +∞ до -∞ четырехугольником или, что равноценно, круга - шестиугольником возникают погрешности в длинах и площадях. Результаты подсчетов погрешностей сведены в таблицу. Линейные сплайны - это вписанный и описанный многоугольники (шестиугольники для круга).
Таблица погрешностей в процентах
|
Вид аппроксимации |
Вписанный |
Описанный |
По Чебышеву |
В среднем |
|
Длина |
-4,507 |
+10,266 |
+2,35 |
+9,96 |
|
Площадь |
-17,30 |
+10,266 |
-5,00 |
±0,00 |
При приближении по Чебышеву необходимо равенство абсолютных величин отклонений ломаной линии от кривой:
|
|δ1| = |δА| = |δ2| = |δВ| = |δ3| |
(10) |
Эпюра напряжений и эпюра деформаций показаны на рис. 4. Индексы ясны из сравнения рис. 4 с рис. 3 Обозначим
|
|
(11) |
то есть
|
|
(12) |
В (11) и (12) σbC = Rb.расч - расчетное сопротивление бетона сжатию при изгибе в отличие от экспериментально найденного Rb.эксп (рис. 3).
Уравнение равновесия проекций внутренних усилий (рис. 4) имеет вид
|
|
(13) |
или в безразмерном виде
|
|
(14) |
где
![]()
|
Апроекц. = φА·ψА + (1 - φА)·(1 + ψА) + (φС - 1)·(1 + ψС) |
(15) |
Уравнение равновесия моментов
![]()
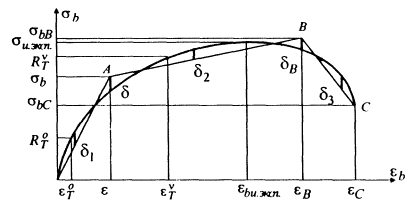
Рис. 3. Аппроксимация диаграммы σb - εb
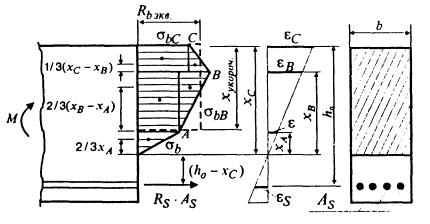
Рис. 4. Усилия и деформации в нормальном сечении
|
|
(16) |
или в безразмерном виде
![]()
где
|
|
(17) |
Связь между упрощенным и уточненным способами расчета
Для перехода от уточненного к упрощенному способу расчета необходимо найти Rи.прив и хукор из условия эквивалентности получаемых по этим способам результатов. Обозначим (см. рис. 4)
![]()
Приравнивая усилия сжатой зоны по обоим способам расчета, получим
|
|
(18) |
Приравнивая моменты усилий сжатой зоны относительно оси растянутой арматуры, будем иметь:
|
|
(19) |
Решение системы (18), (19) дает
![]()
|
|
(20) |
Расчеты показывают, что большие уточнения по сравнению с существующими способами расчета получаются при меньших сечениях высоты сжатой зоны (для балок небольшого размера и плит) и меньших классах прочности бетона, т.е. для элементов массового строительства, на которые расходуется примерно 2/3 общего объема производимой продукции.
ЛИТЕРАТУРА
1. Скоробогатов С.М. О необходимости разработки дополнительной главы СНиП 2.03.01-84* по расчету крупноразмерных железобетонных конструкций. Изв. вузов: Строительство, 1998. № 3. С. 45-51.
2. Филимошкина Г.И., Попов Г.И. Новые результаты испытаний на внецентренное сжатие бетонных призм разных размеров с различной прочностью бетона - См. наст. Сборник статей.
3. Михайлов В.В., Емельянов М.П., Дудоладов Л.С., Митасов В.М. Некоторые предложения по описанию диаграммы деформации бетона при загружении. Изв. вузов: Строительство и архитектура, 1983. № 2. - С. 23-27.
4. Попов Г.И. Приближенный расчет систем с изменяющейся жесткостью на действие кратковременных сил. - М.: ВИА им Куйбышева, 1951. -70 с. (рукопись).
5. Олевский М.Н. О приближении непрерывной функции на заданном интервале кусочно-линейной функцией / ДАН СССР. Т. 82. 1952. № 2.
6. Попов Г.И Приближенный расчет с изменяющейся жесткостью на действие кратковременных сил. – Вестник Военно-Инженерной Краснознаменной Академии им. Куйбышева, Динамические и статические расчеты № 69. - М., 1953 - С 68-109
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Инженер Г. И. Филимошкина,
докт. техн. наук, проф. Г. И. Попов
НОВЫЕ РЕЗУЛЬТАТЫ ИСПЫТАНИЙ НА ВНЕЦЕНТРЕННОЕ СЖАТИЕ БЕТОННЫХ ПРИЗМ РАЗНЫХ РАЗМЕРОВ И РАЗЛИЧНОЙ ПРОЧНОСТИ БЕТОНОВ
В оценке роли бетона в сжатой зоне изгибаемых и внецентренно сжатых железобетонных элементов сложилось два подхода. Первый берет за основу диаграмму σb - εb при центральном сжатии и использует ее с поправками для неоднородного деформирование бетона. Второй исходит из необходимости непосредственных измерений как деформаций, так и напряжений в неоднородно загруженном бетоне.
Опыты экспериментаторы проводили и на моделях, имитирующих сжатую зону бетона изгибаемых или внецентренно сжатых железобетонных элементов, и на различных вставках (датчики) в сжатой зоне изгибаемых элементов, с помощью которых получали эпюры распределения напряжений по высоте сечения сжатой зоны.
Исследование напряженно-деформированного состояния при неоднородном деформировании с помощью металлических вставок затруднено тем, что по длине блока между соседними трещинами нейтральная ось непрерывно меняет свое положение, т.е. непрерывно меняется высота сжатой зоны по длине элемента. Эта «змейка» - нейтральная линия - непрерывно меняет свое положение и во времени (даже при постоянной нагрузке, не говоря уже о возрастающей кратковременной нагрузке). Кроме того, применение металлических вставок весьма трудоемко, так как требует предварительных испытаний вставок. Остается неясным, какое оказывает влияние вставка на продольные и поперечные деформации бетона сжатой зоны, его разрушение и величину разрушающей нагрузки.
С целью изучения напряженно-деформированного состояния сжатой зоны изгибаемых элементов в МАДИ были проведены экспериментальные исследования [1, 2, 3, 4].
Эксперимент включал параллельное испытание образцов-призм на центральное и внецентренное сжатие. В основу был положен двухфакторный эксперимент. Факторами эксперимента являлись: призменная прочность бетона (26, 39, 48, 57, 70 МПа) и размер образца (4×4×16 см, 7×7×28 см, 10×10×40 см, 15×15×60 см и 20×20×80 см).
Работа бетона сжатой зоны
строительных конструкций моделировалась на внецентренно сжатых образцах -
стандартных призмах с размерами ребра поперечного сечения 4, 7, 10, 15, и
Испытания проводились в специальном устройстве [1]. Во время испытаний все поперечное сечение было сжато, а по одной из граней призмы поддерживались деформации, близкие к нулевым Стабилизация нейтральной оси образца в пластической стадии работы достигалась специальным устройством, отклонение нейтральной оси от начального положения составляло не более 2,5 % от размера поперечного сечения образца. Измерение напряжений по высоте поперечного сечения внецентренно сжатого образца проводилось с помощью датчика напряжения, размер которого соответствовал поперечному сечению призмы. Контроль скорости нагружения осуществлялся по приращению напряжений в наиболее загруженной фибре призмы. Деформации в процессе испытаний регистрировались с помощью электротензодатчиков, тензоусилителей «Топаз» и шлейфовых осциллографов Н-115 и НО-43.2. Использование аппаратуры с непрерывной регистрацией деформаций позволило уточнить механизм разрушения бетонов при центральном и внецентренном сжатии.
В результате испытаний призм на центральное и внецентренное сжатие была получена запись продольных и поперечных деформаций бетона и показаний датчика напряжений (при внецентренном сжатии), включая и стадию разрушения бетона. Это позволило построить диаграмму σ - ε для образцов различной прочности и различного размера, определить модуль деформации бетона, предельную деформативность, коэффициент Пуассона, коэффициенты приращения поперечных деформаций и приращения объема [2, 3. 4].
Сопоставление результатов, полученных при центральном и внецентренном сжатии, позволило сделать следующие выводы:
- пластические деформации значительнее проявляются у образцов большего размера и меньшей прочности, поведение образца с увеличением прочности и уменьшением размера приближается к поведению идеально упругого тела;
- модуль деформации бетона при внецентренном сжатии выше, чем при центральном сжатии, и тем выше, чем меньше размер образца;
- диаграммы σ - ε при центральном и внецентренном сжатии для бетонов прочностью 27…70 МПа совпадают только на начальных участках, а в дальнейшем существенно различаются;
- максимальные напряжения в поперечном сечении образцов при внецентренном сжатии превышают призменную прочность, и тем больше, чем больше размер образца и ниже его прочность.
Зависимость предельной деформативности бетона при центральном и внецентренном сжатии от прочности бетона и размера образца иллюстрируется на рис. 1.
Анализ предельной деформативности образцов размером 10×10×40 см при центральном сжатии показывает, что до призменной прочности примерно 40 - 55 МПа наблюдается возрастание значений деформативности бетона, а при дальнейшем увеличении прочности замечено ее снижение. Изменение значений предельной деформативности образцов других размеров с ростом прочности бетона соответствует отмеченной закономерности. Предельная деформативность равнопрочных образцов размером от 4×4×16 см до 20×20×80 см практически линейно увеличивается примерно в 1,5...2 раза (рис. 2).
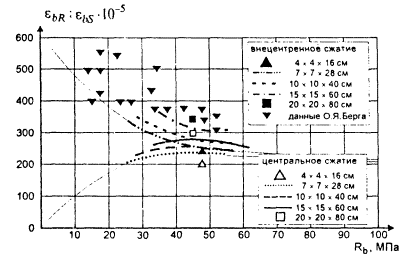
Рис. 1. Предельные деформации бетона σbR и εbR при центральном внецентренном сжатии
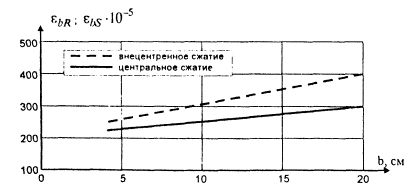
Рис. 2. Изменение предельной деформативности равной прочности и различных размеров
Предельные деформации при внецентренном сжатии определялись как средние деформации крайнего волокна бетона сжатой зоны, расклеенных на лицевой стороне образца. С увеличением прочности бетона предельные деформации при центральном и внецентренном сжатии асимптотически приближаются друг к другу. Предельные деформации при внецентренном сжатии зависят от размера образца; большие предельные деформации наблюдаются у образцов большего размера, аналогичная зависимость свойственна образцам при центральном сжатии. С увеличением прочности предельная деформативность уменьшается (рис. 1).
Оценка
напряженно-деформированного состояния сжатой зоны изгибаемого элемента
проводилась по методике О.Я. Берга, предложенной им для образцов, испытываемых
на центральное сжатие. При рассмотрении результатов испытаний бетонных образцов
на сжатие Бергом О.Я. были выделены две параметрические точки: ![]() нижняя граница
микроразрушений и
нижняя граница
микроразрушений и ![]() - верхняя граница
микроразрушений.
- верхняя граница
микроразрушений.
На рис. 3, 4 показаны зависимости приращений коэффициента поперечных деформаций ΔV при центральном и внецентренном сжатии. На графиках можно выделить три области, которые отделяются одна от другой параметрическими точками.
Первая область
характеризуется уплотнением бетона и соответственно уменьшением объема.
Условной нижней границей является параметрическая точка ![]() , от которой начинается процесс микроразрушений в бетоне.
Вторая область - от уровня
, от которой начинается процесс микроразрушений в бетоне.
Вторая область - от уровня ![]() до уровня
до уровня ![]() - характеризуется
началом разуплотнения материала. В процессе нагружения образуются
микроразрушения, которые постепенно превращаются в микротрещины. Третья область
- за пределами точки
- характеризуется
началом разуплотнения материала. В процессе нагружения образуются
микроразрушения, которые постепенно превращаются в микротрещины. Третья область
- за пределами точки ![]() - характеризуется
интенсивным развитием процесса разрушения структуры бетона и увеличением его
объема.
- характеризуется
интенсивным развитием процесса разрушения структуры бетона и увеличением его
объема.
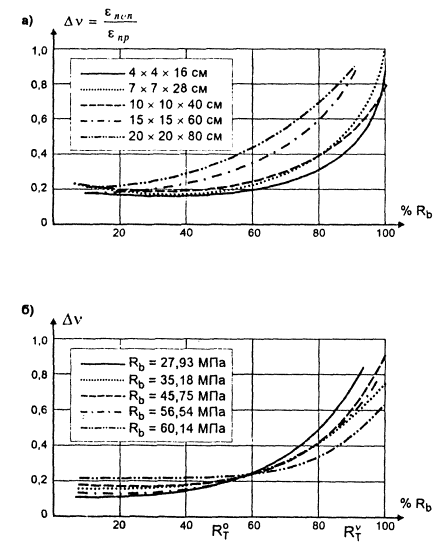
Рис. 3. Изменение коэффициента поперечных деформаций бетона при испытании на центральное сжатие:
а - равнопрочных образцов при Rb = 44÷48 МПа; б - призм размером 10×10×40 см разной прочности
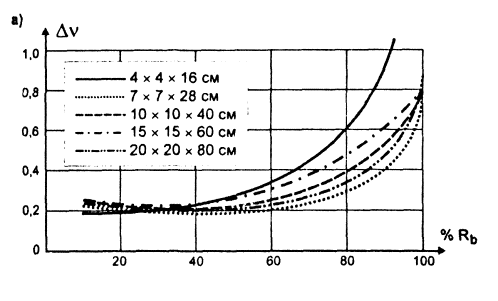
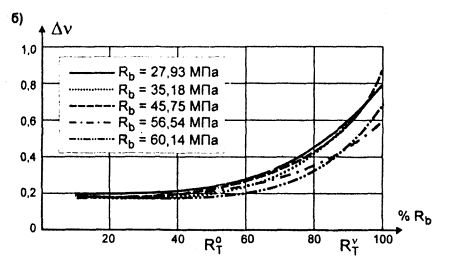
Рис. 4. Изменение коэффициента поперечных деформаций бетона при испытании на внецентренное сжатие:
а) равнопрочных образцов при Rb = 44÷48 МПа;
б) призм размером 10×10×40 см разной прочности
Зависимости
параметрических уровней ![]() и
и ![]() при центральном и
внецентренном сжатии представлены на рис. 5. Анализ кривых
при центральном и
внецентренном сжатии представлены на рис. 5. Анализ кривых ![]() и
и ![]() показывает, что при
центральном сжатии для образцов одного размера по различной прочности граница
микротрещинообразования
показывает, что при
центральном сжатии для образцов одного размера по различной прочности граница
микротрещинообразования ![]() находится в диапазоне
0,38 - 0,55, а граница
находится в диапазоне
0,38 - 0,55, а граница ![]() в диапазоне 0,78 -
0,95. Для образцов одной прочности, но различного размера
в диапазоне 0,78 -
0,95. Для образцов одной прочности, но различного размера ![]() находится в диапазоне
0,38 - 0,55, а
находится в диапазоне
0,38 - 0,55, а ![]() - 0,7 - 0,91.
- 0,7 - 0,91.
Параметрические точки при
внецентренном сжатии располагаются несколько выше, чем при центральном сжатии.
Значения первой параметрической точки ![]() повысились на 12 %, а
второй - на 10 % (рис. 5).
повысились на 12 %, а
второй - на 10 % (рис. 5).
Граница
микротрещинообразования повышается с ростом прочности и уменьшением размера
образца, чем больше образец, тем раньше начинаются необратимые процессы
разрушения структуры бетона. Верхняя параметрическая точка ![]() не является
критерием, характеризующим несущую способность образца. Процесс разрушения
нелинейно развивается до этого уровня и продолжается после него, только
несколько интенсивнее.
не является
критерием, характеризующим несущую способность образца. Процесс разрушения
нелинейно развивается до этого уровня и продолжается после него, только
несколько интенсивнее.
Для высокопрочных
образцов малого размера верхняя граница микротрещинообразования ![]() , вообще,
может быть не обнаружена из-за малого развития пластических деформаций.
, вообще,
может быть не обнаружена из-за малого развития пластических деформаций.
Проведенные исследования образцов при центральном и внецентренном сжатии показывали, что появление первых трещин наблюдается у образцов малых размеров на более поздней стадии деформирования; процесс накопления микродефектов проходит различно в зависимости от размера образца.
Результаты исследований подтверждаются статистической теорией прочности, которая достаточно полно отражает природу масштабного фактора
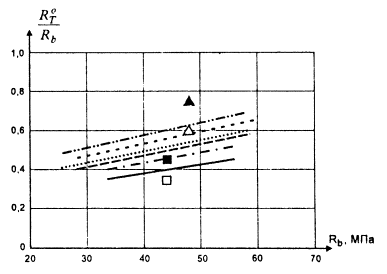
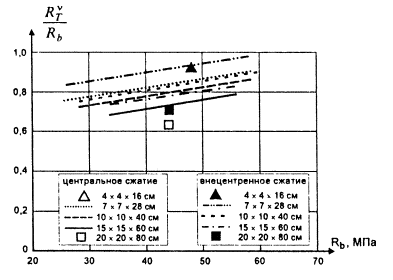
Рис. 5.
Зависимость параметрических уровней ![]() ,
, ![]() при
центральном и внецентренном сжатии
при
центральном и внецентренном сжатии
Влияние масштабного фактора при неоднородном деформировании следует учитывать в расчетах прочности слабоармированных, массивных конструкций, а также тонких плит, особенно из бетонов низкой и средней прочности. Учет этого фактора может дать экономию материалов.
ЛИТЕРАТУРА
1. Садов Б.В., Викторов Б.И., Филимошкина Г.И. Устройство для определения напряженно-деформированного состояния образцов при внецентренном сжатии: Авторское свидетельство. № 1545142, 1989.
2. Викторов Б.И., Садов Б.В., Филимошкина Г.И. Напряженно-деформированное состояние бетонов при центральном сжатии. Сб. науч. тр. МАДИ // Сопротивление элементов железобетонных конструкций действию статических и динамических нагрузок. - М., 1984. - С. 26-33.
3. Викторов Б.И., Садов Б.В., Филимошкина Г.И. Влияние масштабного фактора на прочность бетонов при внецентренном сжатии. Сб. науч. тр. МАДИ // Совершенствование методов расчета строительных конструкций. - М., 1987. - С. 23-26.
4. Садов Б.В., Филимошкина Г.И. Основные закономерности поведения бетонов при неоднородном сжатии. Сб. науч. тр. МАДИ // Совершенствование строительных конструкций и методов их расчетов. - М., 1988. - С 59-67.
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Канд. техн. наук, доц. И.Е. Марьясина
ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ИЗГИБАЕМЫХ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ МЕТОДОМ ПОКООРДИНАТНОГО СПУСКА НА ПЭВМ
В общем объеме сборных железобетонных конструкций производственных и гражданских зданий удельный вес изгибаемых элементов весьма значителен. К ним относятся сборные ригели, балки, панели; они входят в состав покрытий и междуэтажных перекрытий зданий. Автоматизация проектирования изгибаемых железобетонных элементов и легко осуществляемая при этом оптимизация их сечений дают возможность сократить сроки проектирования конструкций и получить экономию строительных материалов и денежных средств.
При автоматизации процесса проектирования задача подбора сечений железобетонных изгибаемых элементов решается инженером и ПЭВМ совместно. Проектировщик обращается к ПЭВМ для выполнения расчетной части работы. Таким образом, ПЭВМ как бы выполняет работу расчетной группы. При этом ведущая роль в процессе проектирования остается за человеком. Решение задачи состоит из последовательного обмена информацией между инженером и ПЭВМ. Результаты счета выдаются на экран и могут быть выведены на печатающее устройство.
Предоставляя инженеру возможность участвовать в процессе проектирования для принятия решения, можно осуществить автоматизацию в условиях существующей системы традиционного проектирования и получить экономичные конструкции. При этом проектировщик освобождается от многих трудоемких процессов, скорость выполнения расчетов возрастает во много раз, исключаются ошибки технического характера. Проектировщик сам может оперативно и непосредственно вводить данные, менять их значения, получать на экране промежуточные результаты и при необходимости их корректировать. В результате счета ПЭВМ выдает на экран ряд проектных решений, на основании анализа которых инженер может выбрать практически оптимальную конструкцию по заданному критерию
Как известно, требования действующего СНиПа [2, 3] по проектированию железобетонных конструкций при подборе сечения предельной арматуры ограничиваются условием, чтобы изгибающий момент от внешних нагрузок М не превосходил внутреннего момента Мсеч, воспринимаемого сечением, то есть чтобы соблюдалось условие М ≤ Мсеч. При этом величина ΔМ = (Мсеч·М) в нормах не нормируется.
Естественно, что при такой постановке вопроса решение задачи проектирования неоднозначно, так как значения геометрических характеристик и характеристик материалов можно задавать различными способами. При этом для каждого набора данных по размерам поперечного сечения элемента и характеристик материалов можно найти соответствующие значения необходимой площади арматуры Аs.
Для получения сечения, экономичного по расходу продольной арматуры, необходимо, чтобы момент сечения Мсеч, наиболее близко соответствовал бы внешнему моменту М, т. е. чтобы разность ΔМ = (Мсеч·М) была минимальной. Принято считать, что сечение продольной арматуры А подобрано удачно, если разность между моментом сечения и внешним моментом не превышает 3,5 %, т.е. если ΔМ = (Мсеч·М) < 3…5 %.
Однако на практике при традиционном проектировании без ПЭВ обычно ΔМ при подборе рабочей продольной арматуры Аs не проверяют, а ограничиваются соблюдением требования, чтобы подобранная арматура Аs была не меньше требуемой по расчету Аs, т.е. чтобы выполнялось неравенство Аs ≥ Аs. Такой метод подбора арматуры может привести к перерасходу стали.
На кафедре аэропортов и конструкций МАДИ разработана программа RIGEL предназначенная для решения задачи на ПЭВМ типа IBM PC XT/AT и совместимых с ними [4]. Программа реализована в системе Turbo Pascal. Алгоритмы расчета составлены в соответствии с требованием норм по проектированию железобетонных конструкций и Рекомендациями НИИЖБа [1].
Работа по программе RIGEL организована следующим образом.
Сначала решается задача проектирования изгибаемых железобетонных элементов в прямой постановке, когда по заданной расчетной схеме ригеля, размерам его поперечного сечения, характеристикам материалов (бетона и арматуры) и величине расчетного внешнего изгибающего момента М с помощью формул СНиПа определяется необходимая площадь сечения продольной арматуры Аs.
На экран дисплея выдаются таблицы сортамента арматуры, таблицы расчетных сопротивлений бетона и стали в соответствии с рекомендациями норм, а также таблицы рекомендуемых размеров поперечного сечения балок с учетом требований унификации.
Проектировщик с помощью курсора выбирает из таблиц нужные параметры.
После ввода исходных данных программа RIGEL переходит в режим счета и определяет требуемую площадь продольной арматуры As. Текущее значение Аs выдается на экран.
На каждом этапе расчета проверяются условия ξ ≤ ξR и μ ≥ μmin.
Используя таблицу сортамента, инженер подбирает арматуру As, руководствуясь требованием, чтобы As была не меньше, чем требуемая по расчету As. т.е. чтобы As ≥ As. На этом подбор продольной арматуры при ручном счете заканчивается.
После первоначального подбора арматуры А программа RIGEL продолжает работу для определения рационального армирования ригеля продольной арматурой.
Для этого задача проектирования решается в обратной постановке - в режиме поверочного расчета, когда определяется несущая способность ригеля Мсеч, при первоначально подобранной арматуре As.
С учетом дискретности сортамента арматуры может быть подобран ряд комбинаций As, которые будут удовлетворять условию As ≥ As. Все они будут удовлетворять требованиям СНиПа, однако наиболее экономичным будет тот, для которого ΔМ будет минимальным.
Проектирование рациональной конструкции ригеля ведется методом последовательных приближений. Первоначально намечаемое количество и диаметр подобранных по сортаменту стержней продольной арматуры As проверяются расчетом. На его основе вносятся уточнения в конструкцию, подбирается другое количество стержней и, возможно, другого диаметра так, чтобы суммарная площадь арматуры As ближе подходила к требуемой As. После уточнения арматуры As снова выполняется расчет и так до тех пор, пока ΔМ не превысит 3…5 % или будет близко к этому.
Используя программу RIGEL, можно, кроме того, проанализировать влияние различных факторов на экономические показатели проектируемой конструкции и выявить параметры, которые оказывают наибольшее влияние на материалоемкость изгибаемых железобетонных конструкций.
Продолжая работу по программе RIGEL, можно определить, сохранится ли необходимая несущая способность балки, если понизить классы бетона и арматуры в соответствии с рекомендациями СНиПа, а также возможность уменьшить размеры поперечного сечения с учетом требований унификации с целью получить экономию бетона и стали.
Сечение ригеля, полученное в результате проведенного анализа, будет практически оптимальным по критерию материалоемкости. Подобранное поперечное сечение ригеля с указанием рекомендуемых классов бетона и арматуры, количества и диаметра продольной арматуры выдается на экран / печать.
Программа RIGEL, как и любая задача проектирования, решаемая с помощью ЭВМ, универсальна в том смысле, что параметрам конструкции, содержащимся в исходных данных, могут придаваться любые значения с помощью программы RIGEL можно решать множество конкретных проектных задач с различными пролетами, размерами поперечных сечений (ширины и высоты балки) для балок из бетона и арматуры различной прочности при разных величинах внешнего момента.
Исходным данным в программе RIGEL присвоены следующие обозначения:
М - внешний изгибающий момент, кН·м;
h - высота сечения элемента, см;
b - ширина сечения элемента, см;
а - расстояние от растянутой грани элемента до центра тяжести растянутой арматуры, см;
Rb - расчетное сопротивление бетона, МПа;
γb2 - коэффициент условий работы бетона;
α - коэффициент, принимаемый равным для тяжелого бетона 6,85; используется при вычислении характеристики сжатой зоны бетона ω;
Rs - напряжение в арматуре, МПа, принимаемое для элементов без предварительного напряжения;
μmin - минимальный процент армирования, принимаемый для балок равным 0,05 %; рекомендуемый процент армирования для балок составляет 1 - 2 %.
Результаты расчетов выдаются на экран в виде текстовой и цифровой информации после каждого шага выполнения программы.
На экран / печать выводится исходная информация, в которой полностью отражаются все этапы расчета при каждом изменении параметров.
Если при заданных ограничениях не удается обеспечить несущую способность ригеля, то на печать выдаются рекомендации перейти к двойному армированию, или к тавровому сечению, или применить предварительно напряженную арматуру с соответствующим изменением классов бетона и арматуры.
Для диалога пользователь-компьютер достаточно элементарного знакомства с клавиатурой ПЭВМ.
ЛИТЕРАТУРА
1. Рекомендации по оптимальному проектированию железобетонных конструкций. - М.: НИИЖБ, 1981. - 170 с.
2. СНиП 2.03.01-84. Бетонные и железобетонные конструкции / Госстрой СССР. - М.: ЦИТП Госстроя СССР, 1985 - 79 с.
3. Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов (без предварительного напряжения) / ЦНИИпромзданий, НИИЖБ - М: ЦИТП Госстроя СССР, 1989. -192 с.
4. Марьясина И.В., Марьясина Т.Д. Методические указания по применению ЭВМ в курсовых и дипломных проектах по строительным конструкциям. Выпуск 12 - М.: МАДИ, 1995.
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Канд. техн. наук, доц. С.С. Ловшин
ПРОЦЕСС АВТОМОБИЛИЗАЦИИ И ЕГО АСПЕКТЫ, СВЯЗАННЫЕ С КАПИТАЛЬНЫМ СТРОИТЕЛЬСТВОМ И РАЗВИТИЕМ ИНФРАСТРУКТУРЫ ОБЪЕКТОВ ДОРОЖНО-ТРАНСПОРТНОГО КОМПЛЕКСА
Потребность в осуществлении эффективных, надежных, удобных и безопасных транспортных сообщений и перевозок постоянно присутствует на всем пути развития человеческой цивилизации. На их развитие и обеспечение во все больших масштабах общество постоянно направляло и направляет значительные объемы имеющихся у него ресурсов и средств. На протяжении последних двух столетий, когда начали появляться большие возможности комплексного развития науки, теории и практики и на этой основе - создания разнообразных видов техники и технологий, организации промышленности, разнообразных видов производств, направлений строительства и других областей человеческой деятельности, стало возможным совершить ряд революционных прорывов, перевернувших существовавшие ранее представления о транспортных средствах, путях, сообщениях и перевозках. Одним из таких качественно принципиально новых прорывов стала автомобилизация. Процесс автомобилизации общества, начавшийся около ста лет тому назад с постройки первого прототипа современных автомобилей, в настоящее время охватывает подавляющее большинство стран мира, а в наиболее социально, экономически и технически развитых из них он уже принимает массовый характер.
Являясь мощным, опережающим и стимулирующим развитие многих сфер фактором, процесс автомобилизации активно влияет на социальную, экономическую, производственную, культурно-эстетическую, бытовую и другие стороны жизни современного общества, на размещение и развитие его производительных сил. За относительно небольшой по историческим меркам срок процесс автомобилизации привел к коренным изменениям представлений о транспортной проблеме в целом, о транспортных средствах, путях, сообщениях и перевозках, системе обслуживания на транспорте, транспортном строительстве, направлениях его развития, номенклатуре, типологии транспортных объектов - комплексов, зданий и сооружений разнообразного назначения.
Важным показателем процесса автомобилизации, принятым во всем мире, является ее уровень, который измеряется количеством легковых автомобилей, приходящихся на 1000 человек населения страны, региона, города. Расчетный ожидаемый на время ti (в течение года и по годам) уровень автомобилизации в стране равен:
|
|
(1) |
где AM(ti) - общая численность (количество) учтенного (зарегистрированного) парка автомобилей на время ti;
NC(ti) - общая численность населения в стране на время ti.
Вводя и раскрывая ряд параметров, формулу (1) можно представить в виде:
|
|
(2) |
где BM(t0) - общая численность (количество) учтенного парка автомобилей на время t0 (начало очередного года);
bM(ti) - коэффициент списания (естественной убыли) автомобилей на время t (величина переменная, посезонная, поэтапная и т.д.),
0 ≤ bM(ti) ≤ 1
CM(ti) - количество учтенных за период времени Δti = (ti - t0) автомобилей, из числа произведенных за тот же период;
DM(ti) - количество учтенных за период времени Δti = (ti - t0) автомобилей, из числа ввезенных в страну из-за границы за тот же период.
Из рис. 1, на котором показана динамика изменения уровня автомобилизации по годам в разных странах мира, следует, что процесс во всех этих странах имеет однозначный нарастающий характер. Однако автомобилизация, представляющая собой очень важное явление, давшее обществу огромные возможности и открывающее перед ним еще более значительные перспективы в будущем, одновременно с этим породила ряд проблем, требующих часто незамедлительного и даже опережающего решения. В нашей стране это, прежде всего, проблемы наращивания сети современных обустроенных транспортных путей - автомобильных дорог, дальнейшего развития системы и инфраструктуры предприятий, организаций и служб, связанных с эксплуатационным обслуживанием, ремонтом и хранением быстро растущего, особенно в крупных городах, парка транспортных средств, придорожным обслуживанием участников движения - водителей, пассажиров, автотуристов, со сбором, хранением и экспедицией (перевозкой с сопровождением) во все больших объемах грузов разнообразного характера и т.д.
В решении многих из вышеназванных проблем большую роль призвано играть капитальное строительство, осуществляемое с целью создания таких основных недвижимых фондов разнообразных организационных структур (предприятий, организаций, служб и т.п.), функционирующих в составе созданного в нашей стране автомобильного транспорта и всего дорожно-транспортного комплекса (ДТК), входящего в единую транспортную систему [1], как многочисленные разнообразные по назначению комплексы, здания и сооружения (рис. 2).
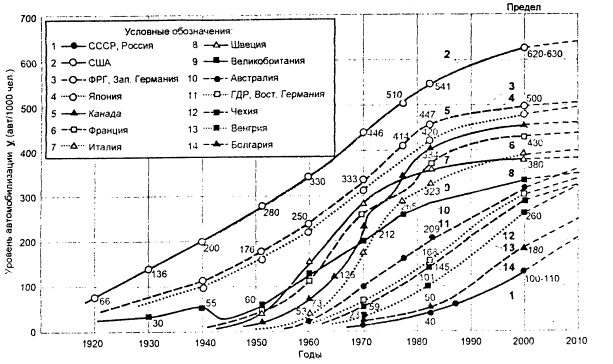
Рис. 1. Динамика изменения уровня автомобилизации
Все строительные объекты, используемые в составе дорожно-транспортного комплекса (ДТК) в городских и внегородских условиях [2 - 6], по функционально-технологическому назначению можно условно разделить на шесть основных групп. Это - комплексы, здания и сооружения обслуживания транспортных средств (первая группа), пассажирских перевозок (вторая группа), грузовых перевозок (третья группа), транспортных путей и сооружений на них (четвертая группа), участников движения и их транспортных средств (придорожный сервис, пятая группа) и специальные сооружения обеспечения безопасности, защиты окружающей среды, шумозащиты, дорожной информации, аварийной связи и т.д. (шестая группа).
К первой группе относятся строительные объекты, предназначенные для осуществления в них и при их использовании технологических процессов, связанных с обеспечением технического обслуживания (содержания, ремонта и хранения) транспортных средств. К таким строительным объектам относятся комплексы, здания и сооружения автотранспортных (АТП) и авторемонтных (АРП) предприятий, баз централизованного технического обслуживания (БЦТО), гаражей (комплексных и некомплексных), специализированных автоцентров (САЦ), станций технического обслуживания (СТО), автозаправочных (АЗС) и газозаправочных (ГЗС) станций и т.д.
Во вторую группу входят строительные объекты, предназначенные для осуществления в них и при их использовании технологических процессов, по характеру связанных с обслуживанием пассажирских перевозок. В эту группу входят комплексы, здания и сооружения автовокзалов и автостанций, отдельно стоящих и совмещенных (пристроенных и встроенных) с вокзалами других видов транспорта (железнодорожным, воздушным, речным, морским), и другие строительные объекты.
К третьей группе принадлежат строительные объекты в виде комплексов, зданий и сооружений транспортно-экспедиционных (ТЭП) и других родственных предприятий, организаций и служб, предназначенных для осуществлений технологических процессов, по характеру связанных с обслуживанием грузовых, в том числе контейнерных, видов перевозок, и для проведения разного рода транспортно-экспедиционных, таможенных и других операций. Кроме этого, строительными объектами, относящимися к этой группе, являются: специализированные грузовые автостанции (ГАС), контейнерные терминалы (КТ), таможенные центры (ТЦ) разнообразных предприятий, организаций и служб.
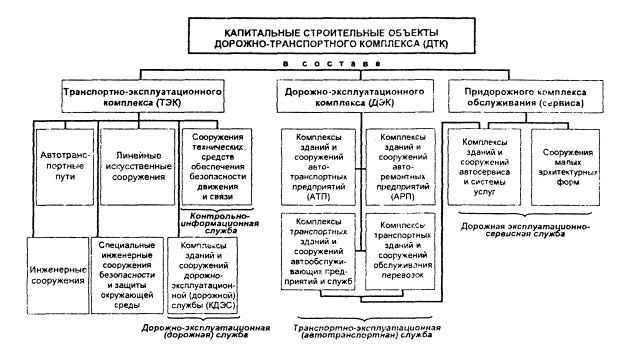
Рис. 2. Основные капитальные строительные объекты в составе дорожно-транспортного комплекса (ДТК)
Четвертая группа объединяет линейные строительные объекты предприятий, организаций и служб, предназначенных для осуществления разного рода технологических процессов по текущему содержанию и ремонту автомобильных дорог и размещаемых на них разнообразных искусственных сооружений. В эту группу входят комплексы, здания и сооружения дорожно-ремонтных строительных участков (ДРСУ) и дорожно-ремонтных пунктов (ДРП), а также стационарные поселки работников автотранспортных, автодорожных и других родственных предприятий, организаций и служб.
К пятой группе относятся линейные придорожные и целевые строительные объекты разнообразных организационных структур (предприятий, организаций, служб и т.д.), предназначенные для предоставления всем участникам движения жизненно необходимых в пути видов услуг, включая техническое обслуживание, ремонт и хранение их транспортных средств. В эту группу входят комплексы дорожного сервиса (КДС), мотели, кемпинги, ротели и другие.
К шестой группе принадлежат специальные линейные строительные объекты в виде инженерных сооружений, предназначенных для обеспечения: безопасности передвижения по городским, внегородским и горным автомобильным дорогам; защиты окружающей среды; шумозащиты селитебных территорий в городах и населенных пунктах от шумовых, загрязняющих и других воздействий автомобильного транспорта, дорожно-информационного обеспечения участников движения - водителей, пассажиров и автотуристов. Такого рода строительными объектами соответственно являются: подземные (ППП) и наземные (НПП) мостового вида пешеходные переходы; подпорные стены и стенки; камне-, лавинозащитные галереи и селезащитные сооружения на горных дорогах; очистные, накопительно-отстойные и другие сооружения; шумоотражающие, шумопоглощающие и комбинированные экраны, сооружения дорожной контрольно-информационной службы, выполненные в виде П- и Г-образных рам, V-образных, стеллообразных и других конструктивных форм, сооружения аварийной телефонной связи и т.д.
Наличие на автомобильном транспорте и в составе всего дорожно-транспортного комплекса все более широкой номенклатуры строительных объектов разнообразных организационных структур (предприятий, организаций, служб и т.д.) делает необходимым проведение всестороннего анализа их решений. Осуществление этого необходимо для отбора самых эффективных, рациональных, наилучшим образом зарекомендовавших себя при строительстве и эксплуатации комплексов, зданий и сооружений и использования опыта в последующих разработках новых поколений строительных объектов [7, 8]. Это позволит в сочетании с другими, проводимыми в разных направлениях мероприятиями, полнее реализовать возможности, предоставляемые автомобилизацией и автомобильным транспортом, и в итоге сделать автомобильные сообщения и перевозки более эффективными, надежными, удобными, комфортными и безопасными.
ЛИТЕРАТУРА
1. Громов Н.Н., Панченко Т.А., Чудновский А.Д. Единая транспортная система. - М.: Транспорт, 1987. - 304с.
2. Фастовцев Г.Ф. Организация технического обслуживания и ремонта легковых автомобилей. - М.: Транспорт, 1989. - 240 с.
3. Голубев Г.Е. Автомобильные стоянки и гаражи в застройке городов. - М : Стройиздат, 1988. -252 с.
4. Сардаров А.С. Архитектура автомобильных дорог. - М.; Транспорт, 1993. - 272 с.
5. Хомяк Я.В., Гончаренко Ф.П., Копилевич С.Л. Инженерное оборудование автомобильных дорог. - М.: Транспорт, 1990. -232 с.
6. Подборка статей из журналов "Автомобильные дороги", "Транспортное строительство" и других научных и научно-производственных периодических изданий за 1990 - 1998 гг.
7. Ловшин С.С, Федулов В.К., Аль бунни Аммар. Пути совершенствования конструктивных решений зданий и сооружений транспортного назначения. Автомобильные дороги. Информационный сборник. Вып. 8. - М.: Информавтодор, 1995. - С. 21-25.
8. Ловшин С.С. Ресурс и работоспособность во времени несущих железобетонных конструкций и систем зданий и сооружений, теоретическая модель их оценки и прогнозирования // Расчет строительных конструкций транспортных зданий и сооружений. - М.: МАДИ. 1994. -С. 142-153.
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Канд. техн. наук, доц. В. А. Серебренников
ИССЛЕДОВАНИЕ ВОПРОСА УСТАНОВЛЕНИЯ КОНКУРЕНТОСПОСОБНОСТИ ПРОЕКТОВ ОРГАНИЗАЦИИ И ПРОИЗВОДСТВА РАБОТ КАК ОБЪЕКТА МАРКЕТИНГА
В условиях рыночной экономики, которая лежит в основе любой производственной деятельности (проектирование, строительство, эксплуатация, реконструкция и т.п.), механизмом ее реализации является рынок, где осуществляется конкуренция между производителями товара - продукта труда, произведенного для продажи (проекты организации и проекты производства работ при строительстве, эксплуатации, реконструкции аэропорта (аэродрома) или его элементов; строительные материалы, изделия, конструкции и т.п.).
В настоящее время строительной организации для получения подряда и подписания контракта на производство работ необходимо получение и заполнение комплекта тендерной документации, участие в торгах совместно с другими строительными организациями, получившими форму тендера, и заключение тендерного комитета на основе проверки и сопоставления условий поступивших тендеров о том, что рекомендуемый ими тендер является наиболее конкурентоспособным.
Конкурентоспособность тендера - это относительная и обобщенная характеристика, выражающая его выгодные отличия от тендера (проекта) конкурентов по техническим и экономическим параметрам, обеспечивающим выполнение всех контрактных обязательств, основными из которых являются заданный уровень качества, сроки выполнения работ и стоимость. Эти параметры находят отражение в проектах организации и производства работ.
При всей значимости информации, содержащейся в тендерной документации, следует отметить отсутствие необходимости предоставления расчетов количественной оценки: основных параметров конкурентоспособности предприятия (рис. 1), которая определяется качеством строительного продукта; стабильности показателей качества при производстве работ (рис. 2); надежности технологических процессов - одного из основных показателей качества (рис. 3).
В связи с этим априори существует определенная вероятность нарушения контрактных обязательств со стороны подрядчика, получившего тендер по качеству, срокам и стоимости выполняемых работ. Например, практика свидетельствует, что при контроле качества выполнения ремонта московских дорог по четырем параметрам: качеству исходных материалов, асфальтобетонных смесей, технологии работ, проектно-сметной документации - было зафиксировано за год свыше 4000 отклонений величины контролируемых параметров от предельно допустимых значений. В итоге дорожно-ремонтные организации, не обеспечившие требуемый уровень качества, были оштрафованы, лишены подряда. Однако принятые санкции не решают проблему в целом, так как устранение допущенного брака требует дополнительных ресурсов и времени, которые неизбежно влияют на сроки и стоимость выполняемых работ (как правило, увеличиваются), то есть условия контракта нарушаются.
Оценка тендерным комитетом и заказчиком надежности технологического процесса, выполняемого потенциальным подрядчиком, до заключения контракта исключает или сводит до минимума возможную опасность (риск) нарушения условий контракта, так как заранее оцениваются свойства технологического процесса обеспечивать выполнение работ (выпуск строительной продукции) с заданными проектом или контрактом уровнем качества, объемами и временем (сроками).
В такой оценке должен быть заинтересован и подрядчик, так как она позволяет объективно определить способность реализовать все обусловленные контрактом обязательства, избежать юридических и финансовых потрясений, сохранить конкурентоспособность строительного производства и, следовательно, обеспечить жизнеспособность предприятия любой формы на рынке строительного производства. Конкурентоспособность строительного продукта (товара) во многом определяет конкурентоспособность самого предприятия.
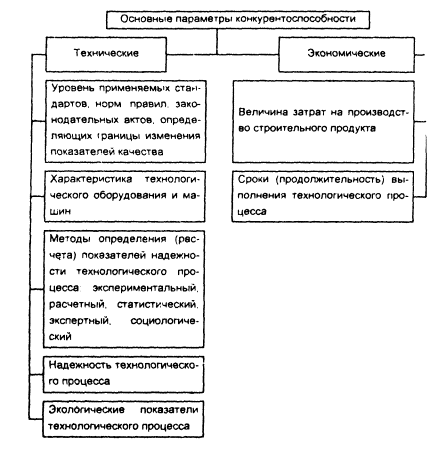
Рис. 1. Основные параметры конкурентоспособности проектов организации и производства работ
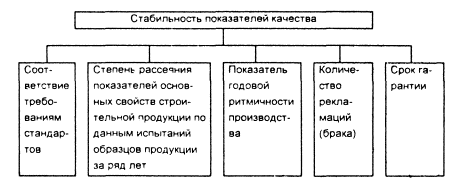
Рис. 2. Стабильность показателей качества строительной продукции
В условиях функционирования тендера и сокращения количества объектов конкуренции возникает необходимость анализа деятельности конкурентов (строительных организаций), который осуществляется специалистами по маркетингу с целью исследования слабых и сильных сторон всех настоящих и потенциальных конкурентов; разработки прогнозов вероятной тактики и стратегии конкурентов в областях технической, технологической, финансовой, экономической и плановой политики. Таким образом, формируется база данных (сведений) о конкурирующих предприятиях и производимом ими строительном продукте - товаре.
Конкурентоспособность проектов организации и производства работ должна устанавливаться на основе расчета основных параметров конкурентоспособности (рис. 1), базирующемся на количественной оценке основных показателей надежности технологического процесса (рис. 3) Расчеты должны выполняться по специальным программам на ПЭВМ.
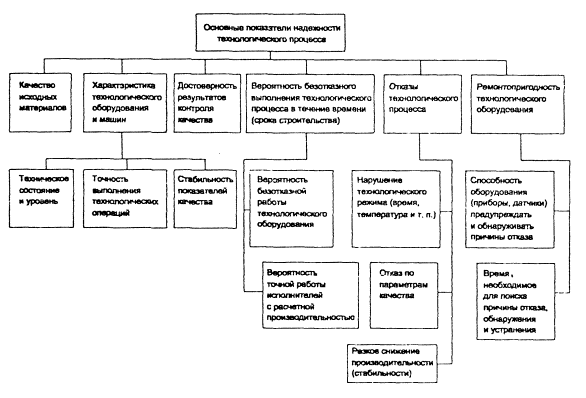
Рис. 3. Основные показатели надежности технологического процесса
Предлагаемые принципы обеспечивают конкурентоспособность строительного продукта за счет предсказуемого высокого качества, которое гарантирует надежность в эксплуатации и победу над конкурентами в борьбе за получение подряда.
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Инженер О.В. Елфимова
К ВОПРОСУ ОПТИМИЗАЦИИ ГЕНЕРАЛЬНОГО ПЛАНА АЭРОПОРТА
Процесс оптимизации при построении генерального плана промышленного объекта представляет собой достаточно сложную архитектурно-строительную задачу, при решении которой увязываются между собой технологические, градостроительные, санитарно-гигиенические, социальные, эстетические и экономические требования. До сих пор этот вопрос, применительно к генеральному плану аэропорта, недостаточно глубоко изучен и дальнейшее его исследование значительно облегчит проектировщику разработку и оценку проектного решения.
Интерес к этой проблеме возник довольно давно. Впервые плоская компоновочная задача была рассмотрена в 30 - 40-х годах при обосновании оптимального раскроя листа на п заготовок. Определяющим критерием была минимизация отходов заготовок. В шестидесятые годы интенсивно решались задачи размещения производства с учетом расстояний до потребителей. При этом минимизировались взвешенные расстояния между объектами, вычисляемые либо в декартовой, либо в прямоугольной метрике (метрике Минковского). Было разработано достаточное количество различных эвристических алгоритмов, сводящихся к размещению точки на плоскости.
Появление математического аппарата К-функции послужило основой для создания алгоритмов и программ размещения геометрических объектов с применением математического аппарата годографов вектор-функции плотного размещения. Это позволило расширить круг формализованных критериев, в той или иной мере учитывающихся при компоновке генеральных планов, и создать метод последовательно-одиночного размещения объектов, широко распространенного в отечественных программных средствах. Первые работы в нашей стране, посвященные решению задачи компоновки генеральных планов, применительно к промышленным предприятиям были выполнены ЦНИИпроектом совместно с МИФИ и МИСИ при участии Л.И. Плужникова, B.C. Нагинской, И.П. Минакова и других [3, 4, 5, 6]. Разработанные авторами программы предусматривают пакетную обработку данных с автоматизированной генерацией вариантов планировки, их частичным перебором и поиском лучшего. Данный подход состоит в применении только автоматической генерации вариантов размещения, когда объекты на плоскости укладываются, начиная с левого нижнего угла зоны размещения, в случайной последовательности, заполняя ограниченную область размещения (способ плотной упаковки), и не уделяет достаточного внимания архитектурным особенностям.
Дальнейшее развитие вычислительных методов и техники привело к новой серии попыток улучшения программных средств. Авторы разработок усовершенствовали применяемые критерии, способы сокращения количества перебираемых вариантов последовательности размещения, предлагали варианты информационного обеспечения задачи.
В 80-е годы рассматривается компоновка внутрицехового оборудования как транспортная задача с использованием графовой модели, включающей в себя внутрицеховые межагрегатные проезды. Колесниченко В.Г. развил это направление [7] и использовал для критериев и целевой функции элементы статистического анализа информации о проектах-аналогах при моделировании строительных комплексов. Хотя его работа ориентирована только на компоновку СТТ аэропорта, она дала толчок к развитию новых подходов в решении вопросов проектирования.
Следует выделить наиболее развитый к настоящему времени комплекс по проектированию генпланов промышленных предприятий, разработанный ЦНИИ проектом при участии ЛГСПИ, РИСИ и др., названный ППП ГПЛ [2]. В рамках проекта программ решаются три группы задач по: определению размеров, конфигурации и места размещения промышленного узла, расчету, трассировке и укрупненной оценке внешних транспортных и инженерных коммуникаций и инженерной подготовке территории. Оптимизация генерального плана производится методом последовательного перебора случайного порядка размещения. Ориентация объектов допускается только параллельно осям координат. Работа ведется в пакетном режиме и вмешательство пользователя в ход решения задачи не предусматривается.
Однако в зарубежной практике автоматизации проектирования опыт проектировщика используется довольно широко. При этом наиболее часто применяются методы, основанные на интерактивном диалоге, где ЭВМ служит в качестве инструмента для облегчения традиционной генерации вариантов, оценки технико-экономических показателей, освобождения человека от чертежных работ. Среди подобных систем можно назвать APEC-CABDS (США), ICES, GSP, CRAFT (США), CLASP (Франция) и др. В качестве информационно-проектировочных средств находят широкое применение базисные экспертные системы с различной программно-структурной и языковой организацией.
В настоящее время в литературе прослеживается «развитие и движение к слиянию двух направлений: теории принятия решений и методологии проектирования, - т.е. ведется поиск путей объединения методов, основанных на логике, и методов использования субъективных суждений. В этом ряду можно отметить работы Григорьева Э.П. [1], разработавшего продуктивную идею инвариантного проектирования, основанную на синтезе этих двух направлений, но не доведенную до практического применения.
Последние отечественные публикации также свидетельствуют о применении элементов графического диалога для решения задачи компоновки генпланов. При этом редактируется сгенерированный машиной вариант генпланового решения. Необходимо отметить, что использование графического диалога не всегда обеспечивает оптимальность решения. На данный момент неизвестны отечественные системы с интерактивной генерацией компоновочных решений. На основе зарубежного опыта прослеживается тенденция к более активному вовлечению проектировщика в процесс компоновки генеральных планов. На основе анализа состояния современных методов автоматизированного проектирования генпланов, можно сделать следующие выводы и наметить пути дальнейшего совершенствования процесса проектирования:
1. Существующие программные средства компоновки могут быть применены лишь к некоторым типам объектов, а для ряда специальных объектов потребуется разработка более совершенных моделей и методов, учитывающих специфику этих строительных комплексов.
2. Важен также учет архитектурной организации пространства с точки зрения неполной модели действия проектировщика.
3. Необходимо обратить внимание на использование в полном объеме возможностей выбора углов ориентации размещаемых объектов, что особенно важно при проектировании сложных сооружений.
4. Разработанные программно-методические средства должны обеспечивать возможность вмешательства проектировщика на промежуточных/ стадиях расчетов и предусматривать в перспективе трансформацию к использованию режима активного графического диалога.
ЛИТЕРАТУРА
1. Григорьев Э.П., Гусаков А.А., Зейтун Ж., Порада С. Архитектурно-строительное проектирование. Методология и организация - М.: Стройиздат, 1986. -240 с.
2. Лопусев П.3., Минаков И.П., Безуевский Ю.М. Методические рекомендации по использованию ЭВМ при разработке схем генеральных планов промышленных узлов. - М.: ЦНИИпроект, 1982. - 24 с.
3. Минаков И.П. Критерии автоматизированной оценки компоновочных решений промышленных узлов: Автореф. дис. канд. техн. наук. - М.: 1972. -20 с.
4. Минаков И.П., Рафалович Н.И., Тимощук В.С. Использование ЭВМ при проектировании генеральных планов и объемно-планировочных решений задач промышленных предприятий. - П.: Стройиздат, 1982. - 111 с.
5. Нагинская В.С. Оптимизация компоновочных решений одноэтажных промышленных зданий. Автореф. дис. канд. техн. наук. - М., 1971. - 120с.
6. Плужников Л.Н. Методы решения задач размещения в автоматических системах проектирования: Автореф. дис. докт. техн. наук. - М. - 34 с.
7. Тригони В.Е., Колесниченко В.Т. Моделирование задачи оптимального размещения зданий и сооружений при проектировании генерального плана аэропорта // Проектирование, строительство и эксплуатация аэропортов. Сборник / МАДИ. - М., 1983. - С. 36-44.
СБОРНИК НАУЧНЫХ ТРУДОВ МАДИ (ТУ)
ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРОЧНОСТИ КОНСТРУКЦИЙ И СООРУЖЕНИЙ АЭРОПОРТОВ
Москва 1999
Инженер А.В. Агеев
ИСПОЛЬЗОВАНИЕ НОВЫХ МАТЕРИАЛОВ В КОНСТРУКЦИЯХ ВАНТОВО-БАЛОЧНЫХ МОСТОВ
Новые материалы, о которых пойдет речь, обладают многими преимуществами. Однако для того чтобы они с успехом заменили традиционные материалы, а следовательно, и могли привести к изменению технологии строительства в такой консервативной сфере, как проектирование мостов, необходимо иметь в виду следующее:
- применение новых конструкционных материалов должно быть тщательно сбалансировано, а преимущества в прочности, жесткости и долговечности использованы полностью. При этом обязательно нужно обеспечить их производство в достаточно больших объемах с целью снижения стоимости, ведь на этапе внедрения затраты всегда велики.
- экономическая оценка должна проводиться на основе всего срока службы материала, при этом учитываются не только первоначальная стоимость (которая весьма велика) и эксплуатационные расходы, но и падение затрат в силу косвенных причин (например, уменьшения пробок автотранспорта за счет снижения количества ремонтных работ).
В последнее время в конструкциях вантовых и висячих кабельных мостов (как, впрочем, и в мостах других систем) все чаще находят применение волокнистые композитные материалы [1, 2, 3]. Они не являются совершенно новыми, углеводородные вещества применяются в других областях с 70-х годов. С их помощью надеются получить повышенный уровень долговечности и надежности, уменьшение эксплуатационных расходов путем сочетания усиленной защиты конструкций с почти идеальными условиями для ремонтных работ.
Чаще всего новые материалы применяются после замены обычных. Использование высокопрочных сталей вместо обычных является примером, когда такой подход возможен, хотя в целях предотвращения усталостных явлений и потери устойчивости может потребоваться серьезный пересмотр известных решений. В случае с волокнистыми материалами приходится фундаментально перепроектировать всю конструкцию с тем, чтобы использовать особые свойства материала.
Многолетние поиски эффективной защиты от коррозии металлических конструкций мостов привели к идее использовать в качестве несущих элементов особые структурные формы из композитного волокнистого материала. Впервые эта идея была воплощена в жизнь при строительстве вантово-балочного моста через реку Тэй в Англии в 1992 году (The Aberfeldy Bridge) [1]. Пилоны и балка жесткости этого моста были собраны из модульных элементов, изготовленных из полимерного композита - углеволоконного пластика. Для усиления (армирования) конструкции может быть использовано стекловолокно, в этом случае композит носит название - фибергласовый пластик.
Конструкционный элемент, например главная балка, имеет ячеистую структуру и по аналогии с «конструктором» состоит из отдельных модулей (рис. 1), которые также выполнены в виде своеобразных сот и объединяются между собой с помощью специальных замковых устройств и клеев на эпоксидной смоле.
Пример такого модуля изображен на рис. 2. Модули изготавливались из длинных заготовок путем их выдавливания и последующей протяжки, что обеспечило им абсолютную точность размеров по всей длине. Кроме того, при таком способе изготовления, когда волокна материала получают строго определенную направленность (по линиям наибольших напряжений), модули приобретают изгибную прочность не хуже, чем у стальных элементов (сопротивление растяжению углеволоконного пластика достигает 1700 МПа).
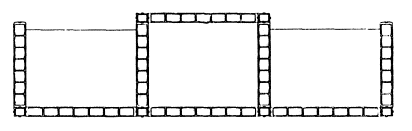
Рис. 1. Поперечное сечение из модулей элемента балки жесткости
К тому же промышленное производство таких конструкций будет сравнительно более дешевым в силу их модульности на микроуровне.

Рис. 2. Ячеистый конструкционный модуль
Технология изготовления
этих конструкций, носящая название The Advanced Composite Construction
System (ACCS), запатентована в
Перечисленные преимущества, а также значительное облегчение процессов сборки конструкций из ячеистых модулей позволят обеспечить высокие уровни безопасности, надежности и долговечности сооружения.
Таким образом, при наличии нескольких типоразмеров ячеистых модулей можно создавать элементы почти любых форм. Нетрудно заметить, что источником этой идеи стали конструкции, созданные самой природой. Как и природные волокнистые структуры, ячеистые элементы весьма устойчивы к повреждениям, обладают повышенной общей устойчивостью и сопротивляемостью к потере местной устойчивости стенок, поскольку сами состоят из таких же сотовых ячеистых модулей, т.е. мы имеем дело с 2-уровневой сопротивляемостью. Совокупность этих свойств с малыми размерами модулей позволяет конструировать достаточно тонкие стенки с достижением высоких уровней напряжений. Преимущества таких совершенных форм контрастируют с ограничениями на этот счет в железобетонных и стальных конструкциях.
Перенеся эти идеи в область большепролетных висячих систем, отметим «горизонты» использования этой технологии:
- легкая и нетрудоемкая в обслуживании балка жесткости. Поскольку она работает совместно с вантово-кабельной фермой, то может для облегчения иметь открытый профиль. Возможно применение и для конструкций пилонов, с учетом их внецентренно сжатой работы [6];
- оболочка из волокнистого материала, работающая совместно с несущими железобетонными или стальными конструкциями, увеличивающая крутильную жесткость системы и придающая ей обтекаемую форму (рис. 3).
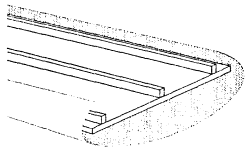
Рис. 3. Оболочка из волокнистого материала
Дальнейшей разработкой этой идеи может стать создание эллиптического «кокона», который будет не только уменьшать крутильные вибрации от ветрового воздействия, но и защищать от атмосферных явлений конструкции балки и автотранспорт [4].
Существует тенденция к применению волокнистых материалов и в качестве основных несущих элементов висячих систем - вант и свободно висящих кабелей [1].
Как известно, при определении расчетного сопротивления растяжению высокопрочной стальной проволоки в вантах из параллельных пучков, подвергающихся цикличным нагрузкам, пользуются следующей формулой [5]:
Rdh = 0,63 Run,
где Run - наименьшее временное сопротивление проволоки разрыву.
В мировой практике современных вантовых мостов предел прочности проволок вант при расчете на эксплуатационные нагрузки уменьшают до:
σтах = 0,55 fур,
где fур - предел текучести стальной проволоки [2].
Такие ограничения вызваны возникновением усталостных явлений в проволоках в местах анкеровки вант, которые появляются в результате продольных и поперечных колебаний вантовых канатов [4, 6]. При увеличении пролета растет и свободная длина ванты, а следовательно, растет амплитуда колебаний. В состав вантовой фермы моста приходится включать поперечные «сшивки» в виде распределительных хомутов, как в мосту Нормандия в устье реки Сена во Франции [3]. Все это приводит к утяжелению конструкций и перерасходу материалов.
Для замены стальной проволоки в вантовых мостах больших пролетов может использоваться арамидное волокно. Арамид, который более известен под торговым названием «кевлар», является полимером на основе ароматических полиамидов (R CO NH2). Он обладает следующими физико-механическими свойствами: сравним по прочности со сталью, легче алюминия, обладает невысокой изгибной жесткостью, великолепной сопротивляемостью усталостным напряжениям, способен поглощать вторичные температурные воздействия и в какой-то мере гасить часть колебаний балки жесткости (табл.). Основным недостатком арамидного волокна является его чрезмерная дороговизна. Проблема коррозионной устойчивости для кевларовых вант становится неактуальной. При монтаже канатов из арамидного волокна отпадает необходимость в тяжелом крановом оборудовании.
Сравнительные физико-механические характеристики композитных полимерных волокнистых материалов, о которых шла речь, приведены в табл. [7]. Удельные прочностные характеристики и модули упругости этих материалов, наряду с их усталостной прочностью при сравнении с показателями высокопрочной проволоки, делают их более привлекательными для создания мостовых конструкций больших пролетов и наводят на мысль, что в случае применения их в качестве несущих элементов потребуются совершенно новые конструкционные и композиционные решения и идеи.
Таблица
Свойства полимерных композитных материалов с высоким содержанием армоволокон
|
Показатель |
Единица измерения |
Стекловолокно |
Углепластик |
Арамид - волокно |
Высокопрочная стальная проволока |
|
Процент армирования |
% |
80 |
72 |
67 |
- |
|
Относительная плотность |
ρ |
2,31 |
1,57 |
1,36 |
7,86 |
|
Сопротивление растяжению |
R, МПа |
950 |
1610 |
1590 |
1820 |
|
Модуль упругости при растяжении |
Е, МПа |
50000 |
136000 |
64300 |
190000 |
|
Удельная прочность |
R/ρ |
44 |
105 |
119 |
24 |
|
Удельный модуль упругости |
Е/ρ |
21,6 |
86,6 |
47,3 |
24,2 |
ЛИТЕРАТУРА
1. В. Richmonds S. H. R. Sham - Present and future developments in cable-supported bridge technology using new materials - IABSE Conference, Deauville, France, 1994.
2. R. Walther - Development of modern
cable-stayed bridges - Ecole Polytechnique Federale de Lausanne,
3. Presentation of the Normandie bridge - IABSE Proceedings - Volume 1 October 1994.
4. Петропавловский А.А., Потапкин А.А. и др. - Вантовые мосты. - М.: Транспорт, 1985. - 224 с.
5. СНиП 2.05.03-84* Мосты и трубы. - М., 1994.
7. P. Head - Advanced Composites for Earthquake Resistant Structures - IABSE Reports, Long-Span and High-rise Structures Symposium, Kobe, 1998.