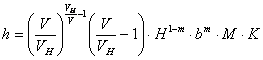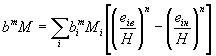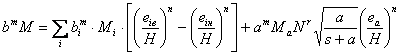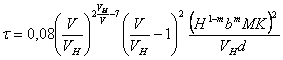ТЕХНИЧЕСКИЕ УКАЗАНИЯ ПО РАСЧЕТУ МЕСТНОГО РАЗМЫВА У ОПОР ЭКСПЛУАТИРУЕМЫХ МОСТОВ
Технические указания утверждены ЦП МПС России в 2001 году
СОДЕРЖАНИЕ
|
|
Юрий Леонидович Пейч |
|
Юрий Владимирович Писарев |
|
Кандидат технических наук, доцент, ведущий научный сотрудник отделения «Путь и путевое хозяйство» ВНИИЖТ |
Доктор технических наук, профессор, заведующий кафедрой «Гидравлика и водоснабжение» МИИТ |
ПРЕДИСЛОВИЕ
Настоящие Технические указания разработаны на основе ВСН 62-69, теоретических, лабораторных, экспериментальных и натурных гидравлических исследований, обобщения литературных источников.
В Технических указаниях дана зависимость для расчета глубины местного размыва у опор мостов на период стабилизации местных деформаций русла из несвязного материала, уточнено определение расчетной ширины опоры моста, определены зависимости для расчета глубины размыва во времени при установившемся и неустановившемся движении потока воды.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Настоящие Технические указания предназначены для использования при эксплуатации мостовых переходов на железных дорогах России в условиях равнинных и предгорных рек с руслами из несвязного грунта и не могут быть использованы для расчета местного размыва у опор мостов селевым потоком, на закарстованных и вечномерзлых грунтах.
1.2. Расчет увеличения глубины местного размыва русла у опор эксплуатируемых мостов производится во времени от начальной до максимальной глубины на период стабилизации размыва. Расчет выполняют при различном характере движения воды в русле водотока: установившемся (постоянная скорость и глубина) и неустановившемся (изменяющаяся во времени скорость и глубина) для расчетных гидрографов паводка или волн попуска (формируются при значительных сбросах воды из водохранилища через плотины ГЭС).
Расчет уменьшения глубин местного размыва у опор мостов на спаде паводка в настоящих Технических указаниях не приводится.
1.3. Местный размыв русла обусловлен повышением скоростей течения воды при обтекании опор мостов. Местный размыв не возникает, если средняя на вертикали предельная скорость течения воды перед опорой моста не превышает непередвигающую скорость течения воды для частиц донных наносов у опоры, в противном случае у опоры моста образуется воронка местного размыва.
Глубина воронки местного размыва от не размытой поверхности дна в створе мостового перехода зависит от формы и размеров опоры моста, скорости, глубины и угла набегания потока, характеристик донных наносов.
1.4. Параметры потока воды перед опорой моста (средняя скорость и глубина на вертикали) определяются в результате расчета общего размыва в створе мостового перехода или на основании гидрометрических работ. Характеристики донных наносов у опоры моста определяются по данным геологических изысканий.
Размыв неоднородного грунта сопровождается явлением самоотмостки дна воронки местного размыва у опоры моста, уменьшающим глубину местного размыва. При слоистой структуре дна расчет местного размыва производится последовательно для каждого слоя грунта.
1.5. Конструкция затопленной части опоры моста и ее фундамента влияет на величину местного размыва. Кругло цилиндрическая форма опоры является базовой. Влияние иных форм элементов различной ширины и высоты, отличных от круглого цилиндра, на величину местного размыва, оценивается введением коэффициента формы и определением расчетной ширины опоры. Косоструйность течения оценивается введением коэффициента косины угла набегания потока. Глубина местного размыва у куста свай высокого свайного ростверка оценивается поправкой к величине размыва у одиночной сваи.
2. РАСЧЕТ МЕСТНОГО РАЗМЫВА У ОПОР ЭКСПЛУАТИРУЕМЫХ МОСТОВ ПРИ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ ПОТОКА
2.1. Средняя на вертикали начальная (непередвигающая) скорость воды перед опорой, при которой частицы грунта у опоры приходят в движение и появляются первые признаки размыва, м/с:
|
|
где V0 - средняя на вертикали неразмывающая на плоском дне скорость потока, м/с. Определяется в зависимости от глубины потока воды и характеристик донных наносов по приложению П. 1;
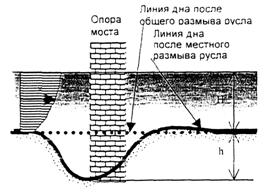
Рис. 2.1. Схема местного размыва русла у опоры эксплуатируемого моста
Кv - переходный коэффициент от скорости воды перед опорой к максимальной у опоры, определяется по формуле
|
|
b - расчетная ширина опоры, м;
Н - глубина потока воды перед опорой над отметкой общего размыва, м.
В формуле (2.2) при Н > 2b следует принимать Н = 2b. Табулированные значения переходного коэффициента Kv в зависимости от b/Н приведены в приложении П. 2.
2.2. Наибольшая глубина местного размыва у опоры моста на период стабилизации деформаций русла при установившемся движении воды, считая от линии дна в створе мостового перехода после общего размыва (рис. 2.1), определяется по формуле, м:
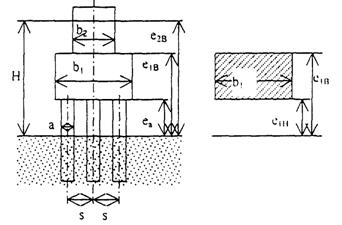
Рис. 2.2. Схема к определению расчетной ширины массивной опоры (справа выделен второй элемент). Вид по направлению скорости потока (по стрелке на рис. 2.5). eiн, eiв - расстояния от линии дна низа (индекс «н») и верха (индекс «в») i-того элемента; bi - ширина i-того элемента массивной опоры.
|
|
где V - средняя на вертикали с глубиной Н скорость установившегося потока воды перед опорой моста, м/с;
М - расчетный коэффициент формы опоры;
К - коэффициент косины, зависящий от угла, образуемого продольной осью опоры с направлением течения перед опорой;
m - показатель степени, зависящей от наличия в потоке влекомых наносов руслоформирующих фракций:
m = 0,5 - при поступлении наносов в воронку размыва (V ≥ V0);
m = 0,6 - при размыве в осветленном потоке (V < V0);
Табулированные значения относительной глубины размыва h/(H1-m·bm·M·К) в зависимости от относительной скорости потока воды V/VН приведены в приложении П. 3.
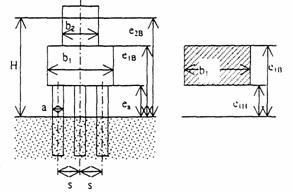
Рис. 2.3. Схема к определению расчетной ширины опоры на высоком свайном ростверке с числом свай в ряду N = 3 (справа выделен первый элемент)
ен = eiв - высота обнаженных свай, равна расстоянию от дна до нижней грани плиты ростверка опоры.
2.3. Произведение расчетных величин bm·M в формуле (2.3) составной конструкции опоры из массивных элементов различной высоты, ширины и формы определяется в зависимости от удаленности элемента от поверхности дна по вертикали и формы элемента в плане из формулы:
|
|
где для i-того элемента опоры и фундамента обозначено (рис. 2.2):
bi - - ширина, м;
М - коэффициент формы;
еiн, еiв - высота в пределах затопления, м, считая от линии общего размыва до нижней и верхней граней элемента. Если элемент опоры заглублен в грунт ниже линии общего размыва, то высотой элемента считается та его часть, которая возвышается над линией общего размыва;
п = 0,25 - показатель степени.
Соотношение между глубиной потока и высотами элементов массивной опоры должно удовлетворять условию:
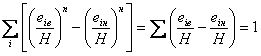
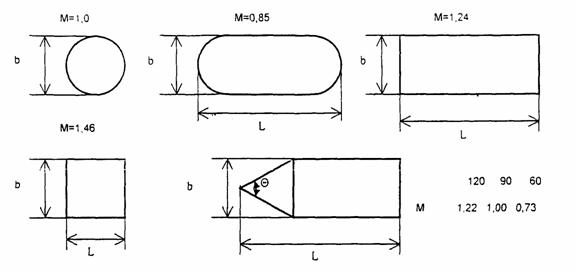
Рис. 2.4. Схема к определению коэффициента формы М элементов конструкции опор постоянного поперечного сечения
2.4. Расчетная ширина опоры b составной конструкции определяется из формулы (2.4) при М = Мi = 1.
2.5. Коэффициент формы М массивной опоры и фундамента с постоянной формой поперечного сечения в зависимости от планового очертания принимают по рис. 2.4.
Расчетный коэффициент формы опоры М составной конструкции определяется из формулы (2.4) при действительных значениях Мi путем деления на величину bm.
2.6. Произведение расчетных величин bm·M в формуле (2.3) опоры составной конструкции из массивных элементов и высокого свайного ростверка (на столбчатых фундаментах, рис 2.3) определяется по формуле:
|
|
(2.5) |
здесь
r = 2/3 - показатель степени;
а - ширина сваи или сваи-оболочки, м;
N - число свай в ряду поперек моста;
s - расстояние в свету между сваями по фасаду моста, м;
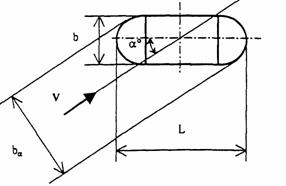
Рис 2.5. Схема к определению коэффициента косины k при косоструйном обтекании опоры
Ма - коэффициент формы отдельной сваи, который принимают равным 1,0 для круглых и 1,46 для квадратных свай;
еа - высота свай над линией общего размыва, м, причем
2.7. При возможной забивке мусором высокого свайного ростверка (реки с карчеходом; потоки, несущие мусор) ширина элемента опоры в части свайного ростверка принимается как массивная с шириной, равной ширине плиты ростверка.
2.8. Коэффициент косины К при косоструйном обтекании опоры (рис 2.5) учитывается при угле косины свыше 10° и определяется по формуле
|
K = (ba/b)m |
где
bа/b = 1 + (L/b - 1)·sin α - проекция ширины опоры на плоскость, перпендикулярную направлению потока, м;
α - угол косины, градусы, образуемый продольной осью опоры с направлением течения перед опорой;
L - расчетная длина опоры, м, определяется для первого массивного элемента конструкции опоры (i = 1), ближайшего к поверхности дна на линии общего размыва из соотношения L/b = Li/bi.
2.9. При слоистом строении русла начальную скорость потока и глубину местного размыва определяют по формулам (2.1) и (2.3). Сначала находят глубину размыва для первого слоя. Если эта глубина захватывает второй слой, то расчет проводят по второму слою, считая, что он выходит на поверхность. Расчет ведут до тех пор, пока будет найден слой грунта, в котором размыв прекратится. Если при расчете какого-либо слоя глубина размыва получится меньше суммы толщин вышележащих слоев, то это означает, что местный размыв прекращается на поверхности рассматриваемого слоя.
3. РАСЧЕТ МЕСТНОГО РАЗМЫВА У ОПОР ЭКСПЛУАТИРУЕМЫХ МОСТОВ ПРИ НЕУСТАНОВИВШЕМСЯ ДВИЖЕНИИ ПОТОКА
3.1. Расчет увеличения глубины местного размыва во времени у опоры моста при неустановившемся движении воды определяют на подъеме паводка.
3.2. Расчетный (ступенчатый) гидрограф паводка должен быть представлен как две гистограммы значений гидравлических параметров - скорости V и глубины Н воды перед опорой моста. Гидравлические параметры на этих гистограммах должны иметь постоянную величину на расчетных интервалах времени Δt (на каждой ступени) с тем, чтобы движение воды на каждой ступени гидрографа описывалось как установившееся.
3.3. Для каждой расчетной ступени гидрографа определяют среднюю на вертикали начальную скорость воды перед опорой VH и наибольшую глубину местного размыва у опоры на период стабилизации деформаций русла h по формулам (2.1) и (2.3).
3.4. Расчет глубины местного размыва у опоры моста в конце каждой расчетной ступени гидрографа паводка производится по исходной глубине местного размыва в начале этой ступени в соответствии с уравнением:
|
F(укон) = F(унач) + Δt/τ |
(3.1) |
где:
унач = hиач/h - относительная глубина размыва в начале ступени гидрографа паводка;
укон = hкон/h - относительная глубина размыва в период окончания гидрографа паводка;
hнач, hкон - глубина размыва у опоры в начале и конце расчетной ступени гидрографа паводка, м;
h - наибольшая глубина местного размыва на период стабилизации деформаций русла, в предположении бесконечной продолжительности ступени гидрографа паводка, определяется по формуле (2.3), м;
Δt - продолжительность ступени гидрографа паводка, час;
τ - масштаб времени нестационарного процесса размыва опоры моста на ступени гидрографа паводка, час;
F(y) - безразмерная интегральная функция.
3.5. Масштаб времени нестационарного процесса размыва опоры моста при установившемся движении потока определяется по формуле, час:
|
|
(3.2) |
где
0,08 - размерный коэффициент пропорциональности, час/с;
d - средний диаметр частиц донных наносов несвязного грунта, м.
Табулированные значения относительного безразмерного масштаба времени
τ/[(H1-m·bmMK)2/VHd]
в зависимости от относительной скорости потока воды VNH приведены в приложении П. 3.
3.6. Безразмерная интегральная функция нестационарного процесса местного размыва имеет вид:
|
|
где
А, В - безразмерные коэффициенты:
|
A = 0,2 + 0,5mG; B = 0,02+0,1mG + 0,165mG2; |
(3.4) |
mG - коэффициент естественного откоса смоченного несвязного грунта, равный отношению заложения к высоте откоса. Для несвязных грунтов в воде mG = 2.
Табулированные значения F(y) по формуле (3.3) при различных значениях относительной ширины опоры b/h представлены в приложении П. 4.
3.7. Методика расчета увеличения глубины местного размыва во времени на расчетной ступени гидрографа паводка состоит в следующем.
3.7.1. По известной начальной глубине размыва hнач и соответствующей относительной величине унач = hиач/h определяют значение функции F(унач) по формуле (3.3) или приложению П. 4.
3.7.2. По формуле (3.2) определяют масштаб времени τ и с учетом заданной продолжительности ступени Δt по формуле (3.1) - значение функции F(укон).
3.7.3. По F(укон) в приложении П. 4 определяют конечную относительную величину укон, а затем искомую конечную глубину размыва hкон = уконh.
3.8. Производится расчет глубины размыва в конце следующей ступени гидрографа, используя в качестве начальной полученную конечную величину местного размыва на предыдущей ступени.
ПРИЛОЖЕНИЯ
П.1. Определение неразмывающих скоростей водного потока V0
За допускаемую скорость потока (среднюю на вертикали V0) принимают наибольшее значение средней скорости течения воды, при которой поток не может вызвать размыва русла.
Физико-механические характеристики грунтов устанавливаются на основании полевых и лабораторных обследований в соответствии с действующими инструкциями.
В особо сложных или ответственных случаях величины допускаемых скоростей течения потока устанавливаются на основании специальных натурных и лабораторных исследований.
При большом содержании взвешенных в воде частиц грунта значения допускаемых скоростей течения потока могут быть повышены при соответствующем обосновании.
Грунт однороден, если
|
d/d10 ≤ 2; |
(П.1) |
где:
d, d10 - средний диаметр частиц грунта и диаметр частиц, мельче которых содержится в грунте по массе 10 %.
Допускаемую скорость для однородного грунта определяют по таблице П. 1 в зависимости от среднего диаметра частиц и глубины потока.
Грунт неоднороден при несоблюдении условия (П. 1). Допускаемую скорость потока для него определяют по формуле
|
V0 = V10×β; |
(П.2) |
где:
V10 - допускаемая скорость для частиц d10, определяемая по таблице П. 1,
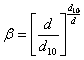
Допускаемые скорости потока для однородных несвязных грунтов
|
d, мм |
V0 м/с при глубине потока в м |
||||
|
0,5 |
1,0 |
3,0 |
5,0 |
10,0 |
|
|
0,05 |
0,46 |
0,48 |
0,53 |
0,55 |
0,57 |
|
0,15 |
0,41 |
0,44 |
0,49 |
0,51 |
0,53 |
|
0,25 |
0,40 |
0,43 |
0,47 |
0.50 |
0,52 |
|
0,37 |
0,40 |
0,43 |
0,48 |
0,50 |
0,53 |
|
0,50 |
0,41 |
0,45 |
0,50 |
0,52 |
0,55 |
|
0,75 |
0,45 |
0,48 |
0,54 |
0,57 |
0,60 |
|
1,0 |
0,50 |
0,54 |
0,60 |
0,64 |
0,68 |
|
2,0 |
0,67 |
0,73 |
0,82 |
0,86 |
0,92 |
|
2,5 |
0,72 |
0,79 |
0,90 |
0,95 |
1,00 |
|
3 |
0,76 |
0,84 |
0,95 |
1,00 |
1,08 |
|
4 |
0,83 |
0,91 |
1,04 |
1,10 |
1,18 |
|
5 |
0,89 |
0,98 |
1,12 |
1,19 |
1.28 |
|
6 |
0,94 |
1,04 |
1,19 |
1,27 |
1,37 |
|
7 |
1,00 |
1,09 |
1,26 |
1,34 |
1,44 |
|
8 |
1,03 |
1,14 |
1,32 |
1,40 |
1,52 |
|
9 |
1.07 |
1,19 |
1,38 |
1,46 |
1,58 |
|
10 |
1,10 |
1,22 |
1,42 |
1,52 |
1,64 |
|
12 |
1,17 |
1,30 |
1,52 |
1,62 |
1,76 |
|
d, мм |
V0 м/с при глубине потока в м |
||||
|
0,5 |
1,0 |
3,0 |
5,0 |
10,0 |
|
|
14 |
1,22 |
1,37 |
1,61 |
1,72 |
1,86 |
|
16 |
1,26 |
1,43 |
1,68 |
1,80 |
1,96 |
|
18 |
1,32 |
1,49 |
1,75 |
1,88 |
2,04 |
|
20 |
1,36 |
1,54 |
1,82 |
1,95 |
2,12 |
|
25 |
1,46 |
1,66 |
1,97 |
2,11 |
2,31 |
|
30 |
1,54 |
1,75 |
2,09 |
2,25 |
2,46 |
|
35 |
1,61 |
1,84 |
2,21 |
2,38 |
2,61 |
|
40 |
1,66 |
1,91 |
2,30 |
2,48 |
2,72 |
|
50 |
1,78 |
2,05 |
2,49 |
2,69 |
2,97 |
|
60 |
1,87 |
2,17 |
2,65 |
2,87 |
3,17 |
|
70 |
1,94 |
2,27 |
2,79 |
3,03 |
3,35 |
|
80 |
2,01 |
2,36 |
2,91 |
3,17 |
3,51 |
|
90 |
2,07 |
2,44 |
3,02 |
3,29 |
3,66 |
|
100 |
2,12 |
2,51 |
3,13 |
3,41 |
3,80 |
|
125 |
2,23 |
2,66 |
3,35 |
3,67 |
4,11 |
|
150 |
2,37 |
2,85 |
3,62 |
3,98 |
4,46 |
|
200 |
2,41 |
2,95 |
3,81 |
4,21 |
4,75 |
|
300 |
2,58 |
3,24 |
4,30 |
4,79 |
5,45 |
П.2. Значения переходного коэффициента Kv от скорости воды перед опорой к максимальной у опоры
Табулированные значения переходного коэффициента Kv от скорости потока перед опорой к максимальной у опоры в зависимости от относительной ширины опоры b/Н по формуле (2.2) приведены в таблице П.2.
Таблица П.2
|
b/Н |
Kv |
b/Н |
Kv |
b/Н |
Kv |
b/Н |
Kv |
b/Н |
Kv |
|
0,5 |
2,32 |
1,1 |
1,97 |
1,8 |
1,74 |
3,0 |
1,52 |
6,0 |
1,3 |
|
0,6 |
2,24 |
1,2 |
1,93 |
2,0 |
1,69 |
3,5 |
1,47 |
7,0 |
1,26 |
|
0,7 |
2,18 |
1,3 |
1,89 |
2,2 |
1,65 |
4,0 |
1,42 |
8,0 |
1,23 |
|
0,8 |
2,12 |
1,4 |
1,86 |
2,4 |
1,61 |
4,5 |
1,38 |
9,0 |
1,21 |
|
0,9 |
2,06 |
1,5 |
1,82 |
2,6 |
1,58 |
5,0 |
1,35 |
10,0 |
1,20 |
|
1,0 |
2,01 |
1,6 |
1,79 |
2,8 |
1,55 |
5,5 |
1,32 |
> 10,0 |
1,20 |
П.3. Значения относительной глубины размыва h/(Н1-mbmMК) и относительного безразмерного масштаба времени τ/[(Н1-mbmМК)/VHd]
Табулированные значения
относительной глубины размыва по формуле (2.3) ![]() и относительного
безразмерного масштаба времени
и относительного
безразмерного масштаба времени ![]() по формуле (3.2) в
зависимости от соотношения скоростей V/Vh даны
в таблице П. 3 и на рис. П. 3
по формуле (3.2) в
зависимости от соотношения скоростей V/Vh даны
в таблице П. 3 и на рис. П. 3
Таблица П. 3
|
|
|
|
|
|
|
|
1 |
2 |
3 |
1 |
2 |
3 |
|
1,00 |
0 |
0 |
4,25 |
1,075 |
0,067 |
|
1,25 |
0,24 |
1,50 |
4,50 |
1,086 |
0,051 |
|
1,50 |
0,44 |
2,01 |
4,75 |
1,096 |
0,040 |
|
1,75 |
0,59 |
1,70 |
5,0 |
1,104 |
0,031 |
|
2,00 |
071 |
1,25 |
5,5 |
1,115 |
0,020 |
|
2,25 |
0,80 |
0,88 |
6,0 |
1,123 |
0,013 |
|
2,50 |
0,87 |
0,61 |
6,5 |
1,129 |
0,0088 |
|
2,75 |
0,92 |
0,43 |
7,0 |
1,132 |
0,0061 |
|
3,00 |
0,96 |
0,30 |
8,0 |
1,135 |
0,0031 |
|
3,25 |
0,99 |
0.22 |
9,0 |
1,135 |
0,0017 |
|
3,50 |
1,02 |
0,16 |
10 |
1,133 |
0,0010 |
|
3,75 |
1,04 |
0,117 |
15 |
1,118 |
0,00013 |
|
4,00 |
1,06 |
0,088 |
20 |
1,104 |
0,00003 |
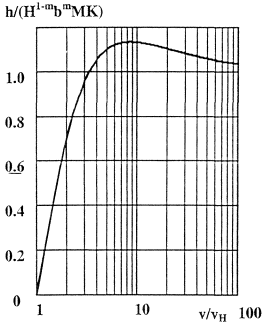
Рис. П. 3. Относительная максимальная глубина размыва h/(Н1-тbтМК) в зависимости от относительной скорости потока воды V VH по формуле (2.3).
П. 4. Значения безразмерной интегральной функции F(y)
Табулированные значения безразмерной интегральной функции F(y) в зависимости от относительной ширины опоры b/h по формуле (3.3) приведены в таблице П. 4 и на рис. П. 4.
Таблица П. 4
|
b/h |
Значения F(y) при относительной глубине y, равной |
||||||||||
|
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,85 |
0,9 |
0,95 |
0,97 |
0,99 |
|
|
0,5 |
0,06 |
0,15 |
0,30 |
0,57 |
1,03 |
1,87 |
2,58 |
3,69 |
5,80 |
7,47 |
11,2 |
|
1,0 |
0,09 |
0,20 |
0,40 |
0,73 |
1,28 |
2,27 |
3,10 |
4,40 |
6,83 |
8,73 |
13,0 |
|
1,5 |
0,12 |
0,26 |
0,49 |
0,38 |
1,53 |
2,63 |
3,63 |
5,09 |
7,35 |
10,0 |
14,8 |
|
2,0 |
0,15 |
0,31 |
0,59 |
1,04 |
1,78 |
3,09 |
4,15 |
5,80 |
8,87 |
11,3 |
16,6 |
|
3,0 |
0,20 |
0,42 |
0,78 |
1,36 |
2,29 |
3,90 |
5,20 |
7,20 |
10,9 |
13,8 |
20,2 |
Рис. П. 4. График для определения функции F(y) в зависимости от относительной ширины опоры b/h по формуле (3.3)
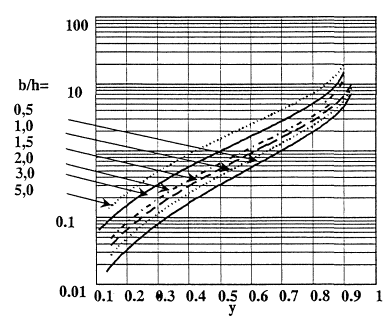
Рис. П. 4. График для определения функции F(y) в зависимости от относительной ширины опоры b/h по формуле (3.3)
П. 5. Примеры расчетов
П. 5.1. Расчеты при установившемся движении водного потока
Пример 1. Определить расчетную ширину b и расчетный коэффициент формы М массивной опоры на рис. 2.2 с одинаковой высотой элементов е3В - е2В = e2B - e1B = e1B. Первый и второй элементы в плане имеют форму прямоугольника, третий элемент имеет овальную форму в плане, косина потока 10°. Ширина элементов относится как b1/b2 = b2/b3 = 1,2. Наносы поступают в воронку размыва (т = 0,5).
Решение. M1 = 1,24; М2 = М3 = 0,85; b1 = 1,44b3; b2 = 1,2b3.
1). Произведение bm·М определяют по формуле (2.4):
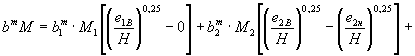
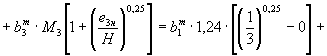
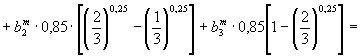
= ![]() ·1,24·0,76 +
·1,24·0,76 + ![]() ·0,85·[0,90 - 0,76] +
·0,85·[0,90 - 0,76] + ![]() ·0,85·[1 - 0,90] = (1,44b3)m·1,24·0,76
+
·0,85·[1 - 0,90] = (1,44b3)m·1,24·0,76
+
+ (1,2b3)m·0,85·0,14
+ ![]() ·0,85·0,1 =
·0,85·0,1 = ![]() ·[1,440,5·1,24·0,76 + (1,2)0,5·0,85·0,14 + 1·0,85·0,1] =
·[1,440,5·1,24·0,76 + (1,2)0,5·0,85·0,14 + 1·0,85·0,1] =
= ![]() ·(1,131
+ 0,13 + 0,085) =
·(1,131
+ 0,13 + 0,085) = ![]() ·1,35
·1,35
Таким образом, bm·М = ![]() ·1,35.
·1,35.
Расчетная ширина опоры определяется при Mi =1:
bm = ![]() ·[l,44m - 0,76 + 1,2m
- 0,14 + 1·0,1] =
·[l,44m - 0,76 + 1,2m
- 0,14 + 1·0,1] = ![]() - (0,91 + 0,15
+ 0.1) =
- (0,91 + 0,15
+ 0.1) = ![]() ·1,16.
·1,16.
Таким образом, bm = ![]() ·1,16, откуда расчетная ширина опоры при т = 0,5: b = b3 (1,16)2 = b3·1,34. (это больше, чем
ширина третьего и второго элементов, но меньше ширины первого).
·1,16, откуда расчетная ширина опоры при т = 0,5: b = b3 (1,16)2 = b3·1,34. (это больше, чем
ширина третьего и второго элементов, но меньше ширины первого).
3) Расчетный коэффициент формы М определяется из уравнений
bm·M = ![]() ·1,35, bm
=
·1,35, bm
= ![]() ·1,16
·1,16
Таким образом, М = 1,35/1,16 = 1,16.
Проверка соотношения между глубиной потока и высотами элементов массивной опоры:
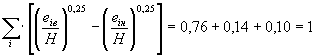
Ответ: расчетная ширина опоры b =1,34·b3; расчетный коэффициент формы опоры моста М = 1,16.
Пример 2.
Определить
коэффициент косины К массивной опоры
длиной L =
По формуле (2.6) определяем
К = [1 + (L/b - 1) sin α]m = [1 + (12/3 - 1)sin 20°]0,5 = 2,140,5 = 1,46.
Ответ. К = 1,46.
Пример 3.
Определить глубину местного размыва на период стабилизации деформаций русла у опоры эксплуатируемого моста.
Опора
расчетной шириной b =
По таблице П. 1 определяем допускаемую неразмывающую скорость на плоском дне:
V0 = 1,02 м/с. Из рисунка 2.4 определяем М = 1. По формуле (2.1) и (2.2) находим:
![]()
VNH = 1,0/0,44 = 2,27. V/V0 = 1,0/1,02 = 0,98.
По условию 0,98 < 1,0 - поток осветленный, т = 0,6.
Коэффициент косины определяется по формуле (2.6): К = 0 при α = 0.
По табл. П. 3
определяется путем линейной интерполяции относительная глубина, при VNH =2,27, равная h/(H1-m·bm·MK) = 0,80. Поскольку h/(60,4·30,6·1) = h/4,00, то h = 4,00×0,80 =
Ответ h =
Пример 4.
Определить, на какую
величину изменится глубина местного размыва русла у опоры моста за периоды
времени Δtj = 1; 3;
5; 10; 24 и 48 часов при установившемся движении потока воды для условий
примера 3, если начальная глубина местного размыва дна у опоры моста при t0 = 0 составляет h0
=
Решение.
Из примера 3 глубина местного
размыва русла у опоры моста на период стабилизации деформаций русла h =
По таблице П. 3 при V/VH = 2,27 определяем относительный масштаб времени τ нестационарного процесса, равный 1000τ/[(H1-m·bm·MK)2·/VH·d] = 0,88. Поскольку 1000 τ/[(60,4·30,6·1)2/0,44·0,003] = τ/12,0, то масштаб времени τ = 0,88·12,0 = 10,5 часа. Расчет изменения глубины местного размыва у опоры моста проведем в табличной форме:
|
Δt, час |
0 |
1 |
3 |
5 |
10 |
24 |
48 |
|
Δt/τ |
0 |
0,10 |
0,29 |
0,48 |
0,95 |
2,28 |
4,57 |
|
y0 = h0/h |
0,62 |
- |
- |
- |
- |
- |
- |
|
F(y0) |
0,80 |
- |
- |
- |
- |
- |
- |
|
F(yj) = F(y0) + Δt/τ |
0,80 |
0,90 |
1,09 |
1,28 |
1,75 |
3,08 |
5,37 |
|
yj |
0,62 |
0,64 |
0,68 |
0,70 |
0,75 |
0,84 |
0,93 |
|
hj = yj·h, м |
2,00 |
2,05 |
2,18 |
2,24 |
2,40 |
2,70 |
3,00 |
Примечание: F(y) определено по таблице П. 3 при b/h =3,0/3,2 = 0,95
Ответ: За 48 часов глубина размыва у опоры моста возрастет с h0 =
|
tj, час |
0 |
1 |
3 |
5 |
10 |
24 |
48 |
|
hj, м |
2,0 |
2,1 |
2,2 |
2,3 |
2,4 |
2,7 |
3,0 |
П. 5.2. Расчеты при неустановившемся движении водного потока
Пример 5.
Определить изменение глубины местного размыва русла у опоры моста во времени при прохождении расчетного гидрографа паводка в условиях обычной асинхронности увеличения скорости и подъема уровня воды в реке (Интервал времени Δtj, Скорость потока V, Глубина потока Н):
|
Δtj, час |
0 - 24 |
24 - 36 |
36 - 48 |
48 - 72 |
72 - 96 |
96 - 168 |
|
V, м/с |
0,9 |
1.5 |
2,0 |
2,3 |
2,0 |
1,6 |
|
Н, м |
3,0 |
3,5 |
4,0 |
5,0 |
5,5 |
6,0 |
Опора моста
расчетной шириной b =
Решение.
Решение ведем в табличной форме для каждой ступени гидрографа паводка.
1). Определение глубины на период стабилизации деформаций и масштаба времени процесса размыва.
|
Δtj, час |
0-24 |
24-36 |
36-48 |
48-72 |
72-96 |
96-168 |
|
V0 по прил. (П. 1), м/с |
0,95 |
0,96 |
0,97 |
1,00 |
1,01 |
1,02 |
|
KV по ф-ле (2.2) |
2,01 |
2,09 |
2,15 |
2,24 |
2,27 |
2,32 |
|
VH по ф-ле (2.1) м/с |
0,47 |
0,46 |
0,45 |
0,45 |
0,44 |
0,44 |
|
V/VH |
2,13 |
3,26 |
4,44 |
5,11 |
4,45 |
2,84 |
|
|
0,75 |
0,99 |
1,080 |
1,107 |
1,080 |
0,93 |
|
m по п. 2.2 |
0,6 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
|
H1-m·bm·MK, м |
3,00 |
3,24 |
3,46 |
3,87 |
4,06 |
4,24 |
|
Глубина на период стабилизации, м |
2,25 |
3,20 |
3,73 |
4,48 |
4,38 |
3,94 |
|
|
1,12 |
0,22 |
0,055 |
0,029 |
0,055 |
0,37 |
|
[(H1-m·bm·MK)2·/VH·d] / 1000 |
6,38 |
7,45 |
8,51 |
10,64 |
11,70 |
12,77 |
|
Масштаб времени τ, час |
7,15 |
1,64 |
0,47 |
0,31 |
0,65 |
4,72 |
2) Определение изменения глубины местного размыва в конце расчетной ступени гидрографа паводка
|
Δtj. час |
0-24 |
24-36 |
36-48 |
48-72 |
72-96 |
96-168 |
|
Δt/τ |
3,35 |
7,31 |
25,5 |
77,4 |
36,9 |
15,2 |
|
Начальная глубина hнач, м |
1,50 |
2,07 |
3,07 |
3,73 |
4,28 |
4,38 |
|
Унач = hнач/h |
0,67 |
0,64 |
0,82 |
0,87 |
0,98 |
1,11 |
|
F(Унач) |
1,25 |
0,85 |
2,20 |
3,3 |
9,0 |
- |
|
F(Укон) = F(Унач) + Δt/τ |
4,63 |
8,16 |
27,7 |
80,7 |
45,9 |
- |
|
Укон |
0,92 |
0,96 |
1,00 |
1,00 |
1,00 |
- |
|
Конечная глубина hкон = Укон h, м |
2,07 |
3,07 |
3,73 |
4,28 |
4,38 |
Замыв воронки размыва |
Ответ Увеличение глубины размыва дна у опоры моста при увеличении скорости и подъема уровня воды в реке:
|
Время, сутки |
0 |
1 |
2 |
3 |
4 |
5 |
|
Глубина размыва, м |
1,50 |
2,07 |
3,73 |
4,28 |
4,38 |
замыв |
П. 5.3. Расчет при слоистом строении русла
Пример 6.
Определить глубину
местного размыва у опоры моста на период стабилизации деформаций дна при
установившемся движении потока, в русле слоистого сложения. Скорость потока
перед опорой моста V = 1,8 м/с, глубина Н =
По данным геологических изысканий донные отложения у опоры имеют 2 слоя с характеристиками: глубина залегания 1 слоя - 0….3,5 м; 2 слоя -3,5….8,0м. Фракционный состав донных отложений:
1 слой
|
Диаметр сит, мм |
0,15 |
0,25 |
0,40 |
1,0 |
|
весовые остатки на ситах, % |
8,0 |
17,0 |
70,0 |
5,0 |
2 слой
|
диаметр сит, мм |
2,0 |
3,0 |
5,0 |
10,0 |
|
весовые остатки на ситах, % |
5,0 |
35,0 |
40,0 |
20,0 |
Решение.
1). По Приложению П. 1. определяют средний диаметр частиц грунта d, диаметр d10, неразмывающую скорость V0 и начальную скорость VH по каждому слою:
1 слой:
d =
(0,15·8 + 0,25·17 + 0,40·70 + 1,0·5) /100 =
d10 = 0,15 + (10 -
8)·(0,25 - 0,15)/(17 - 8) =
d/d10 = 0,38/0,17 = 2,23 > 2,0
Таким образом, грунт 1 слоя неоднороден;
2 слой:
d = (2-5 +
3·35 + 5·40 + 10·20)/100 =
d10 = 2,0 + (10 -
5)·(3 - 2) / (35 - 5) =
d/d10 = 5,15/2,17 = 2,37 > 2,0
Таким образом, грунт 2 слоя неоднороден.
Определение скорости V0 (по Приложению П. 1.).
1 слой:
β1 = (2,23)1/2,23 = 1,43V0 = 0,51 м/с, V0 = 0,51·1,43 = 0,73 м/с.
2 слой:
β2 = (2,17)1/2,17 = 1,43V10 = 0,90 м/с, V0 = 0,90·1,43 = 1,29 м/с.
Определение скорости VН при V/Н = 4,5/8,0 = 0,56 (по Приложению П. 2.):
1 слой: KV = 2,28VH = 0,73/2,28 = 0,32 м/с
2 слой: KV = 2,28 VH = 1,29/2,28 = 0,57 м/с
2). По Приложению П. 3 определяют максимальную глубину местного размыва (считая от линии неразмытого дна) в каждом слое.
1 слой: V/VH = 1,8/0,32 = 5,6, V/V0 = 1,8/0,73 = 2,46 > 1,0, тогда m = 0,5.
h/(H1-m·bm·MK) = 1,117. (H1-m·bm·MK) = 80,5·4,50,5·1,16·1 =
h = 1,117·6,96 =
Поскольку глубина местного размыва в 1 слое больше его мощности (толщины 1 слоя), то размыв будет продолжен во 2 слое.
2 слой:
V/VH = 1,8/0,57
= 3,15, V/V0
= 1,8/1,29 = 1,39 > 1,0 тогда m = 0,5. h/(H1-m·bm·MK)
= 0,98, (H1-m·bm·MK)
= 80,5·4,50,5·1,16·1 =
h =
0,98·6,96 =
Поскольку глубина местного размыва в 2 слое меньше глубины залегания его подошвы, то местный размыв закончится во 2 слое.
Ответ. При слоистом сложении дна русла реки
максимальная глубина местного размыва у опоры моста составит h =