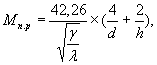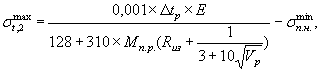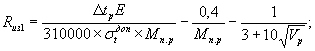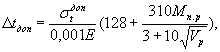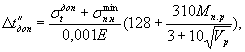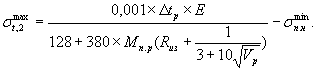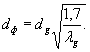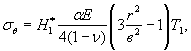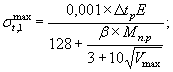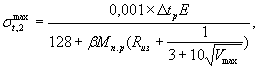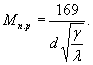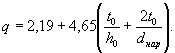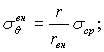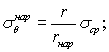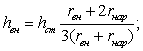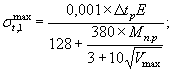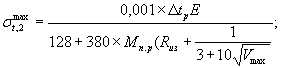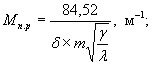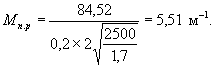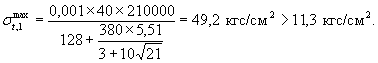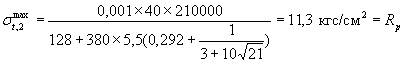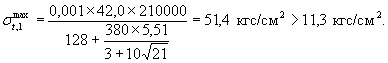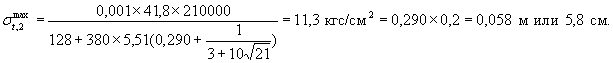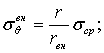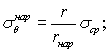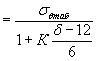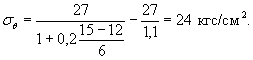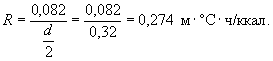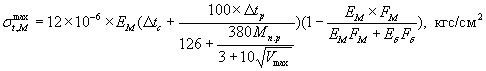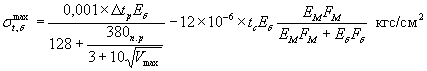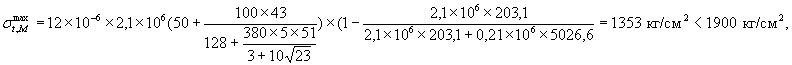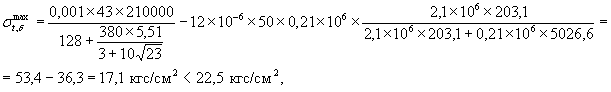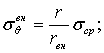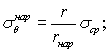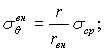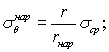ВСЕСОЮЗНЫЙ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ТРАНСПОРТНОГО СТРОИТЕЛЬСТВА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО
РАСЧЕТУ ТЕМПЕРАТУРНЫХ И
УСАДОЧНЫХ НАПРЯЖЕНИЙ В
ЖЕЛЕЗОБЕТОННЫХ ЦИЛИНДРИЧЕСКИХ
ОПОРАХ
МОСТОВ
Москва 1979
Содержание
ПРЕДИСЛОВИЕ
Из инженерной практики известны различные конструктивно-технологические мероприятия по борьбе с температурно-усадочными трещинами в период изготовления, строительства и эксплуатации мостовых опор. Однако эти мероприятия могут быть действенными только тогда, когда они основаны на надежном расчёте напряжений в конструкции, вызываемых изменением температуры и усадкой бетона. Настоящие Методические указания позволят проектировщикам и строителям не только полнее представить особенности напряженного состояния опор от тепловых и влажностных воздействий на разных стадиях, но и количественно оценить последствия этих воздействий. Таким образом, открывается возможность еще в процессе проектирования запланировать мероприятия по снижению температурно-усадочных напряжений до безопасных величин.
методические указания состоят из уточненных и систематизированных методик расчёта цилиндрических железобетонных опор транспортных сооружений на температурные и влажностные воздействия, которые разработаны в ЦНИИСе.
Указания по расчету температурных и усадочных напряжений в круглоцилиндрических железобетонных опорах составлены впервые, поэтому некоторые их положения в дальнейшем могут быть уточнены и дополнены. Для более полного выявления возможных недостатков необходим опыт применения разработанных методик в практической деятельности проектировщиков и строителей. В связи с этим все практические замечания, присланные в адрес института, будут полезны.
В разработке Методических указаний принимали участие д-р техн. наук В.С. Луньянов, канд. техн. наук В.П. Величко, инк. А.И. Цимеринов и кандидаты техн. наук И.И. Денисов, Л.Н. Лосев.
Зам. директора института Н.В. Смирнов
Руководитель отделения
вычислительной техники, методов исследований
и испытаний конструкций и материалов В.Л.
Бурнштейн
I. ОБЩИЕ ПОЛОЖЕНИЯ
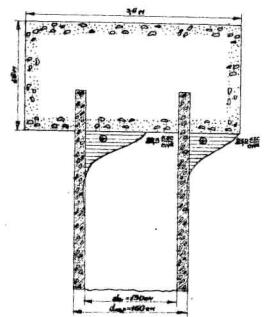
Настоящие методические указания предназначены для использования при проектировании и строительстве мостовых опор с цилиндрическими элементами из бетона и железобетона в надфундаментной части. Они могут найти применение также при строительстве других железобетонных конструкций кольцевого и круглого поперечных сечений, применяющихся в транспортном строительстве: стоек надарочного строения мостов, колонн-оболочек гидротехнических сооружений, центрифугированных опор контактной сети и т.д.
Методические указания позволяют оценить степень опасности появления трещин от изменения температуры и усадки бетона как в стадии изготовления и строительства, так и в стадии эксплуатации.
К настоящему времени накоплен большой опыт проектирования в строительстве таких сооружений, однако опыт их эксплуатации свидетельствует о наличии в них ряда дефектов. Наиболее распространенным дефектом свай-оболочек, цилиндрических стоек и столбов являются различные трещины. Во многих случаях, особенно в суровых климатических условиях, трещины в цилиндрических элементах снижают долговечность сооружения в целой в связи с возможностью проникновении влаги к арматуре и коррозии ее.
исследования причин трещинообразования в железобетонных цилиндрических элементах ведутся в ЦНИИСе под руководством д-ра техн. наук, проф. В.С. Лукьякова с 1960 г. Они показали, что немаловажную роль в возникновении трещин играют температурные и влажностные воздействий при изготовлении цилиндрических конструкций, в период монтажа сооружения, а затем, и особенно, при его эксплуатации. В результате таких воздействии в элементах возникают сложные напряженные состояния, которые непрерывно изменяются и при неблагоприятном стечении обстоятельств приводят к трещинообразованию.
При разработке методик широко применялся метод гидравлических аналогий на интеграторах ИГЛ1, впервые примененный автором для расчете температурного режима и температурных напряжений в бетонных опорах мостов2.
___________________
1. См. В.С. Лукьянов. Гидравлические приборы для технических расчётов. Изв. Отделения технических наук АН СССР, 1939, № 2.
2. См. B.C. Лукьянов. Борьба с появлением температурных трещин в бетонных мостовых опорах. Научно-исследовательский институт пути и строительства НКПС. М., Трансжелдориздат, 1937.
Методики расчёта, включенные в Методические указания, составлены отдельно для элементов сплошного, составного и кольцевого сечений.
Для элементов сплошного поперечного сечения учитывается различие напряженных состояний маломассивных сборных железобетонных столбов заводского изготовления (диаметром до 1,2 м) и массивных, бетонируемых на месте (диаметром до 4 м). В первом случае считается, что элементы прошли термовлажностную обработку и не имеют после нее остаточных напряжений. Расчётное термонапряженное состояние в них возникает дважды сразу же после выдачи из камер пропаривания или из цеха на склад и затем в процессе эксплуатации. Во второй случае (массивные столбы) в отличие от первого (маломассивные) при расчёте напряжений, возникающих на стадии эксплуатации, учитываются остаточные напряжения, возникшие еще в процессе изготовления. Для массивных столбов даны методики расчёта температурных и усадочных напряжений в различных зонах по высоте.
Методики расчёта элементов составного и кольцевого сечений распространяются на железобетонные оболочки диаметром до 3 м включительно с заполненной (бетоном или смесью песка с мазутом) полость и пустотелые.
методика расчета температурных напряжений в оболочках, заполненных бетоном, позволяет учитывать неодинаковость бетона оболочки и заполнения по величине модуля упругости и температурного коэффициента линейного расширения, а также изменения температурных деформаций влажного замораживаемого бетона по сравнению с деформациями при положительной температуре. Эти изменения, вызываемые замерзанием воды, содержащейся в порах бетона, влияют на величину температурных напряжений и могут быть охарактеризованы зависимостью коэффициента линейного расширения влажного бетона от температуры. Полученная расчётная величина температурных напряжений включает как напряжения от общего, равномерного по объему понижения температуры неоднородного цилиндра, так и от ее неравномерного изменения в радиальном направлении.
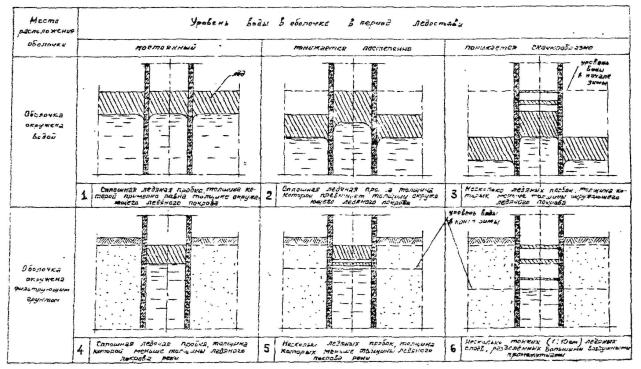
Методика расчёта пустотелых оболочек позволяет определить величину температурных напряжений в процессе изготовления с пропариванием и в момент пропитки горячими гидроизоляционными составами, а также оценить возможность трещинообразования в различных зонах по высоте в процессе эксплуатации под воздействием колебаний температуры воздуха, уровня воды, под влиянием солнечной радиации и косого дождя, ледяных пробок и в результате высыхания бетона на воздухе.
Расчётные воздействия следует выбирать в каждом конкретном случае на основе анализа предполагаемых условий эксплуатации опоры, климатических и гидрологических характеристик постового перехода.
Рассматриваются нормальные напряжения, действующие в кольцевом направлении (тангенциальные) и в продольном, вдоль оси (осевые). Первые вызывают продольные, а вторые - кольцевые трещины.
Допускается определять суммарные температурно-усадочные напряжения σ (в кгс/см3) по формуле
σ = σU+Kσt,
где σU - усадочные напряжения в какой-либо зоне по высоте опоры, кгс/cм2;
σt - температурные напряжения в той же зоне, кгс/см2;
K - коэффициент, принимаемый при суммировании усадочных и температурных напряжений в пустотелых оболочках в надводной зоне и над грунтом:
в районах с влажным климатом K = 0,75;
в районах с климатом умеренной влажности K - 0,3;
в районах с сухим климатом K = 0,1,
При суммировании усадочных и температурных напряжений в оболочках в других зонах и в опорах сплошного сечения принимается K = 0,5.
Сложение температурно-усадочных напряжений следует производить только с напряжениями, возникающими от воздействия:
собственного веса частей сооружения, расположенных выше рассматриваемого сечения;
усилий предварительного напряжения вертикальной арматуры;
усилий предварительного напряжения спиральной арматуры.
Методические указания основаны на следующих допущениях:
влияние арматуры на напряженное состояние от изменения температуры и усадки бетона не учитывается;
бетон рассматривается как однородный изотропный материал;
модуль упругости и коэффициент Пуассона считаются не зависящими от возраста бетона, температуры и величины напряжений;
ползучесть бетона при расчётах температурных и усадочных напряжений учитывается коэффициентами релаксации, полученными на основе теории упруго-ползучего тела;
коэффициент линейного расширения бетона во всех случаях, за исключением указанных в п. 3.3.1 , считается постоянным;
массивные монолитные столбы считаются забетонированными без перерывов и изолированными от соприкосновения с водой в течение всего периода твердения;
ввиду достаточной высоты опоры места сопряжений с оголовком (подферменником, ригелем и пр.) и фундаментом не оказывают влияния друг на друга и на зону, примыкающую к горизонту воды.
Поскольку настоящие методические указания имеют целью предотвратить трещинообразование, то в качестве расчётной рассматривается стадия работы опоры до появления трещин, и напряженное состояние от изменения температуры и усадки бетона после появления трещин не рассматривается.
В качестве критерия трещиностойкости принимается нормативное RH и расчетное Rp сопротивления бетона растяжению или предельно допустимые напряжения σtдоп в зависимости от типа конструкции, вида расчетного воздействия, характера влияния трещин на условия эксплуатации сооружения, а также качества бетона.
Наиболее жесткими условиями эксплуатации опор следует считать условия, которые имеют место в зоне переменного горизонта воды на зарегулированных реках и в акваториях морских портов, где в морозы возможны резкие внутри суточные колебания уровня воды. критерием трещиностойкости в этих случаях является Rр. В большей части остальных случаев, если напряжение равно или несколько меньше Rp, то вероятность возникновения трещин очень мала и практически можно считать, что трещины не возникнут. Если же полученные по расчету напряжения превышают Rн, то вероятность появления трещин превышает 0,5, и поэтому следует позаботиться о снижении напряжений путем применения тех или иных мероприятий. Напряжения, величина которых находится в пределах между Rp и Rн, приведут к образованию трещин только в случае плохого качества бетона, а также вследствие непредвиденного изменения внешних условий. Для бетона в раннем возрасте (в стадии изготовления) критерием трещиностойкости является σtдоп - величина переменная, зависящая от возраста.
2. РАСЧЁТ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЙ В ЦИЛИНДРИЧЕСКИХ ОПОРАХ В СТАДИИ ИЗГОТОВЛЕНИЯ И СТРОИТЕЛЬСТВА
2.1. Столбы сплошного сечения
2.1.1. В период выдачи из камер пропаривания или из цеха на склад
Для оценки опасности трещинообразования столбы, подвергающиеся термообработке в камерах пропаривания, должны рассчитываться на максимальные растягивающие температурные напряжения в периферийных слоях, возникающие от резкого охлаждения столбов после выдачи из камер или из цеха на склад.
Максимальные растягивающие напряжения σtmax (в кгс/см2) определяются по формулам:
а) для столбов без предварительного напряжения или имеющих его только в продольном или кольцевом направлении
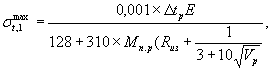 (1)
(1)
а перепад температуры
Σtp = tб.р-tв.р, С°, (2)
где tб.р - наивысшая температура бетона внутри столба непосредственно перед выдачей из камеры проваривания или из цеха на оклад, °С. За tб.р не следует принимать температуру поверхности столба, так как в этом случае не будут учтены начальные растягивающие напряжения в периферийных слоях бетона, образующиеся в процессе термообработки столбе в камерах пропаривания. Величина tб.р определяется экспериментально;
tв.р - минимальная среднесуточная температура воздуха, возможная один раз за 5 лет в течение того времени года, в который будет производиться термообработка столбов данного размера в паровых камерах,°С. Величина tв.р определяется по данным местных управлений гидрометеорологической службы или по соответствующим климатологическим справочникам;
Е - модуль упругости бетона в момент выдачи столбов из камеры пропаривания или из цеха на склад, кгс/см2
Мп.р - расчётный модуль поверхности столба, м, определяемый по формуле
где γ - объемная масса бетона, кг/м3;
λ - коэффициент теплопроводности бетона, ккал/м. ч. °С
d - диаметр столба, м;
h - высота, м;
Rиз - термическое сопротивление опалубки и теплоизоляции на поверхности столбов, м2.°С, ч/ккал,
Vp - максимальная скорость ветра, определяемая на тех же условиях, что и tв.p, м/с;
б) для столбов с предварительным напряжением одновременно в продольном и кольцевом направлениях:
где σп.н.min - минимальное из двух сжимающих напряжений, вызванных предварительным натяжением продольной и кольцевой арматуры, кгс/см2.
В целях обеспечения трещиностойкости столбов величина σtmax не должна превышать допустимой величины σtдоп. Для снижения σtmax до σtдоп рекомендуются следующие меры:
снижение диаметра столбов (d);
повышение теплопроводности бетона за счет повышения водонасыщения бетона, например, поливом водой столбов в камере пропаривания;
устройство закрытых складов, где столбы защищены от воздействия ветра;
выдерживание столбов на буферных складах с регулируемой температурой воздуха, при которой в любой момент времени σtmax ≤ σtдоп
покрытие столбов съемной теплоизоляцией с величиной термического сопротивления Rизmax (м3·°C·ч/ккал) не менее:
а) для столбов без предварительного напряжения или имеющих его только в продольном или кольцевом направлении
б) для столбов с предварительным напряжением одновременно в продольном и кольцевом направлениях
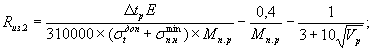 (6)
(6)
Необходимая толщина теплоизоляции l0 из материала с коэффициентом теплопроводности λm (в ккал/м °С. ч) определяется по формуле
l0 = Rизmax × λm (7)
Эффективность рекомендуемых мер проверяется расчётом по формулам (1) и (4).
Величина допускаемой разницы температур бетона и воздуха Σtдоп (в °С) при выдача столбов из камер пропаривания или из цеха на склад рассчитывается по формулам:
а) для столбов без предварительного напряжения или имеющих его только в продольном или кольцевом направлении
где σtдоп - допускаемые напряжения растяжения бетона к моменту выдачи столбов из камеры, кгс/см2. Принимается по опытным данным, полученным для бетона, изготовленного из тех же материалов, того же состава и теми же методами, что и бетон столба.
При отсутствии опытных данных величину σtдоп бетона принимают по действующим нормативным документам.
В случае, если столбы при выдаче из камеры подвергаются увлажнению по специальной технологии, член 3+10√Vр в формулах (8) и (9) считается бесконечно большим числом;
б) для столбов с предварительным напряжением одновременно в продольном и кольцевом направлениях
где Vp - скорость ветра, м/с. На открытых складских площадках, не защищенных от ветра, величина Vp определяется в результате замеров анемометром, а в складах, закрытых от ветра, принимается равной 0,5 м/с.
Для повышения Δtдоп рекомендуется применять те же меры, что и для снижения σtmax до σtдоп.
Допустимую расчётную температуру воздуха tв.p (в °С) при выдаче столбов из камер или из цеха на склад следует определять по формуле
tв.p = tб.р-Δtдоп. (10)
Если фактическая температура наружного воздуха ниже tв.p, то столбы следует предварительно выдерживать на буферном складе до тех пор, пока tб.р постепенно снизится до величины
tб.р = tв.p+Σtдоп (11)
При этом температуру воздуха на буферном складе следует регулировать так, чтобы в любое время перепад между температурой в центре столба и воздуха не превышал Δtдоп. При отсутствии буферного склада необходимо применять съемную теплоизоляцию с термическим сопротивлением Rизmax, определяемым по формулам (5) и (6). Теплоизоляция может быть удалена после снижения tб.р до требуемой величины.
Пример 1. Завод должен изготовить и поставить в сентябре-ноябре железобетонные, предварительно не напряженные столбы диаметром 0,8 м и высотой 10 м. По технологическим условиям на заводе столбы перед выдачей из камер имеют наивысшую температуру бетона tб.р = + 48°С.
Бетон столба имеет следующие характеристики: σtдоп = 22,5 кгс/см2; γ = 2400 кг/м3 λ = 1,7 ккал/м °С ч, Е = 210000 кгс/см2; Rиз = 0.
По данным ближайшей метеостанции за 5 лет, в течение сентября-ноября возможна минимальная среднесуточная температура воздуха tв.p = - 20°С и максимальная скорость ветра Vp = 25 м/с.
Требуется рассчитать максимальные растягивающие температурные напряжения σtmax в периферийных слоях, возникающие от охлаждения при выдаче столбов из камеры на открытую складскую площадку.
По формуле (2) Δtp = 48 - (-20) = + 68 °С.
По формуле (3) 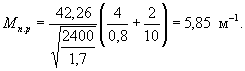
По формуле (1) 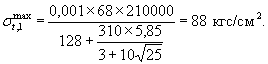
Для снижения σtmax с 88,0 кгс/см2 до σtдоп = 22,5 кгс/см2 необходимо применить съемную теплоизоляцию. Ее максимальное термическое сопротивление Rиз,1max в м2°С ч /ккал по формуле (5) будет равно
![]()
При съемной теплоизоляции из строительного войлока с λm = 0,045 ккал/ м °С ч ее толщина определяется по формуле (7) и равна l0 = 0,26×0,045 = 0,012 м, или 1,2 см.
Тогда по формуле (1)
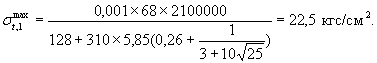
Пример 2. Определить, можно ли отгружать столбы из камер на открытую складскую площадку при температуре наружного воздуха -5°С и скорости ветра 1 м/с. Все остальные условия те же, что и в примере 1.
По формуле (8)
![]()
По формуле (10) tв.р = 48-28,6 =+ 19,4 °С.
Следовательно, столб нельзя выдавать на воздух при температуре -5°С и скорости ветра 1 м/с. Это станет возможным лишь после выдержки на буферном складе до тех пор, пока tб.р постепенно снизится с +48°С до -5 +28,6 = 23,6°С. Температура воздуха на буферном складе должна регулироваться так чтобы в любой момент времени перепад между температурой в центре столба и воздуха не превышал Δtдоп = 28,6 °С.
2.1.2. При бетонировании на месте строительства
от выравнивания температур после отвердевания бетона, т.е. при переходе к равномерному распределению температур, в опоре возникают температурные напряжения. Эти напряжения можно рассчитать, если вначале определить максимальный перепад температур Т0. Между осью опоры и ее поверхностью в период затвердевания бетона; когда в опоре еще не возникают напряжения. соответствующая кривая распределения температур по диаметру опоры называется кривой нулевых напряжений.
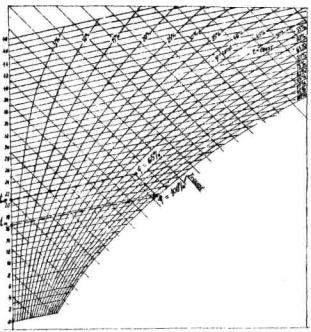
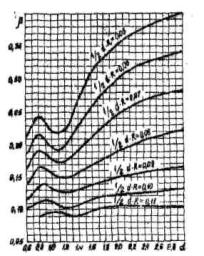
Величина перепадов температур Т0 определяется по графику (рис. 1) в зависимости от типа опалубки и отношения tб/tв где
tб - средняя температура бетона, укладываемого в опору, и
tв - средняя температура наружного воздуха в течение первых пяти суток после окончания бетонирования. Эти графики построены для бетонных опор диаметром 160-400 см, бетонируемых при положительных температурах воздуха, но ими можно пользоваться и для опор, бетонируемых в зимнее время. Для опор, бетонируемых зимой методом "термос" (при этом кривая нулевых напряжений имеет выпуклый вид), Т0 определяется по кривой 2 для значений tб/tв = 4,25, а для опор, бетонируемых зимой с применением периферийного прогрева (кривая нулевых напряжение имеет вогнутый вид), для значения tб/tв = 0,24.
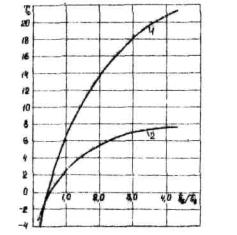
Рис. 1. График определения перепада температур между осью и поверхностью опор для построения температурной кривой нулевых напряжений:
1 - для металлической (скользящей) опалубки; 2 - для деревянной опалубки
После того, как величина Т0 определена, рассчитывают распределение температурных напряжений по радиусу опоры по формуле
![]() (12)
(12)
где Н0* = 0,135d - 0,037 - коэффициент релаксации напряжений вследствие ползучести бетона; (13)
d - диаметр опоры, м;
α - коэффициент линейного температурного расширении, 1/°С;
ν - коэффициент Пуаccона
в - радиус опоры, см
r - расстояние от оси опоры до точки, в которой вычисляются напряжения, см (0 ≤ r ≤ в).
Пример. Требуется рассчитать температурные напряжения от выравнивания температур после отвердевания бетона в опоре, забетонированной в деревянной опалубке. Температура бетона tб = 20°С. Температура воздуха tв = 5°С. Диаметр опоры d = 300 см. Коэффициент линейного расширения бетона α = 10-5 1/°C; модуль упругости бетона Е = 3,15×105 кгс/см2, коэффициент Пуассона ν = 0,15.
Вначале определяют перепад температур Т0 по кривой 2 рис. 1 для tб/tв = 20/5 = 4 (T0 = 7,6°С).
Далее определяют коэффициент релаксации напряжений при выравнивании температур по формуле (13)
Н0* = 0,135×3,0-0,037 = 0,368.
Затем по формуле (12) определяют температурные напряжения. Например, для поверхности опоры (r = 150 см) получим
![]()
Аналогично вычисляются напряжения в других точках по радиусу опоры. Соответствующая опора напряжений приведена на рис 2, из которого видно, что в поверхностных слоях опоры возникают небольшие сжимающие напряжения. Эти напряжения следует расценивать как положительный фактор, так как они отчасти компенсируют растягивающие напряжения, появляющиеся в поверхностных слоях в стадии эксплуатации (см. п. 3.1.4.), и тем самым снижают возможность трещинообразования.

Рис. 2. Распределение тангенциальных напряжений по диаметру опоры при выравнивании температур после отвердевания бетона
2.2. Пустотелые оболочки
2.2.1. При одностороннем пропаривании изнутри
В результате одностороннего паропрогрева оболочек на открытых полигонах изнутри воздается большая неравномерность распределения температур по толщине стенки в процессе отвердевания бетона. Это может привести к образованию трещин на внутренней поверхности оболочек после остывания. Для предупреждения трещинообразования необходимо так организовать односторонний паропрогрев, чтобы растягивающие напряжения σθ, возникающие на внутренней поверхности после остывания, не превышали нормативное сопротивление бетона оболочки растяжению Rн. Для снижения напряжений рекомендуется применять теплоизоляцию на наружной поверхности или снижать температуру пара.
При отсутствии теплоизоляции на наружной поверхности оболочек во время пропаривания σθ определяется по следующим формулам;
а) при пропаривании в закрытом помещении
![]() (14)
(14)
где Е - модуль упругости бетона оболочки, кгс/см2
Тп- максимальная установившаяся температура пера в оболочке, °C;
Тв - минимальная температура воздуха, омывающего оболочку, °С;
hст - толщине стенки оболочки, м;
б) при пропаривании на открытом воздухе
![]() (15)
(15)
При наличии теплоизоляции на наружной поверхности оболочек во время пропаривания σθ рассчитывается следующим образом:
а) при пропаривании в закрытом помещении
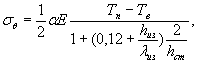 (16)
(16)
где hиз - толщина слоя теплоизоляции, м;
λиз - коэффициент теплопроводности теплоизоляции, ккал/(м. °С ч);
б) при пропаривании на открытом воздухе
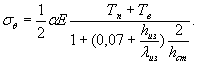 (17)
(17)
Пример 1. Рассчитать растягивающие напряжения на внутренней поверхности оболочки при остывании после одностороннего пропаривания изнутри. Толщина стенки оболочки - 0,1 м, теплоизоляция отсутствует. Температура пара Тп = 66,8°С, температуре воздуха Тв = 20°C. Оболочка пропаривается в закрытом помещении, Марка бетона оболочки 400; коэффициент линейного расширения α = 10-5 1/°С модуль упругости Е = 3,5×105 кгс/см2, нормативное сопротивление растяжению Rн = 25 кгс/см2.
По формуле (14)
![]()
Так как температурные напряжения оказались меньше нормативного сопротивления, то опасность появления трещин отсутствует.
Пример 2. При тех же, что и в примере 1, размерах оболочки и характеристиках бетона Тп = 80°С, а Тв = 10°С. Оболочка пропаривается на открытом воздухе и на имеет теплоизоляции на внешней поверхности. По формуле (15)
![]()
Поскольку в этом случае растягивающие напряжения оказались выше нормативного сопротивления, на внутренней поверхности оболочки после остывания возможно появление трещин. Для уменьшения напряжений необходимо или понизить температуру пара внутри оболочки, или применить теплоизоляцию на внешней ее поверхности (или поверхности опалубочной формы) в период пропаривания.
Проверка эффективности этих мероприятий показана в примерах 3 и 4.
Пример 3. Если в примере 2 понизить Тп с 80°С до 42°С, то при прочих равных условиях σθ, рассчитанное по формуле (15), будет равно
![]()
Таким образом, растягивающие напряжения не будут превышать нормативного сопротивления Rн = 25 кгс/см2.
Пример 4. При тех же, что в примере 2, исходных данных внешняя поверхность оболочки В период пропаривания закрывается теплоизоляцией из дерева толщиной 3 см с коэффициентом теплопроводности λиз = 0,20 ккал/м ч, °С; тогда σθ, рассчитанное по формуле (17), будет равно
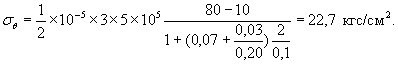
Таким образом, σθ будет меньше нормативного сопротивления.
Наиболее правильным решением является применение в период пропаривания теплоизоляции, так как снижение температуры пара удлиняет процесс термообработки.
2.2.2. В период выдачи из камер пропаривания или из цеха на склад.
Пустотелые оболочки, подвергающиеся термообработке в камерах пропаривания, должны рассчитываться на максимальные растягивающие температурные напряжения σtmax в наружных слоях, возникающие от резкого охлаждения оболочек после выдачи из камер пропаривания или из цеха на склад.
σtmax (кгс/cм2) рассчитывается по формулам:
а) для оболочек без предварительного напряжения или имеющих его только в продольном или кольцевом направлении
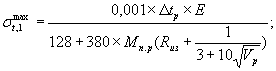 (18)
(18)
б) для оболочек c предварительным напряжением одновременно в продольном и кольцевом направлениях
В формулах (18) и (19) обозначения те же, что и в формулах (1) и (4).
Величина Мп.р (в м-1) для оболочки определяется по формуле
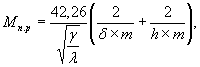 (20)
(20)
где δ - толщина стенки оболочки, м;
h - высота, м;
m - коэффициент, учитывающий заделку торцов оболочек пробками. Для оболочек без заделки торцов m = 1,0 c пробкой на одном торцах m = 1,5, и с пробками на обоих торцах m = 2.
В целях обеспечения трещиностойкости оболочек величина рассчитанных σtmax не должна превышать допускаемой величины σtдоп.
Для снижения σtmax следует принимать меры, рекомендуемые в п. 2.1.1 для столбов. При этом максимальное термическое сопротивление съемной теплоизоляции (в м2 ч °С/ ккал) будет равно:
а) для оболочек без предварительного напряжения или имеющих его только в продольном и кольцевом направлении
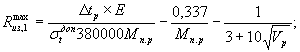 (21)
(21)
б) для оболочек с предварительным напряжением одновременно в продольном и кольцевом направлениях
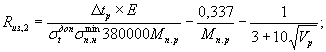 (22)
(22)
Величина допускаемой разницы температур бетона и воздуха при выдаче оболочек из камер пропаривания или из цеха на склад Δtдоп (в °С) должна определяться по формулам:
а) для оболочек без предварительного напряжения или имеющих его только в одном направлении
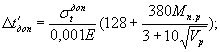 (23)
(23)
б) для оболочек с предварительным напряжением одновременно в продольном и кольцевом направлениях
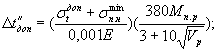 (24)
(24)
В формулах (23) и (24) обозначения те же, что и в формулах (8) и (9). Величина Мп.р определяется по формуле (20).
допустимую расчетную температуру наружного воздуха tв.p перед выдачей оболочек из камер или из цеха на склад следует определять по формуле (10). Если фактическая температура наружного воздуха ниже tв.p, то их следует выдерживать на буферном складе в соответствии с формулой (11). При этом температуру воздуха следует регулировать так, чтобы в любое время перепад между ней и температурой внутри стенки не превышал Δtдоп
При отсутствии буферного склада следует применять съемную теплоизоляцию с максимальным термическим сопротивлением, определяемым по формуле (21) или (22) и толщиной теплоизоляции l0 - по формуле (7). Теплоизоляция ножей быть удалена после снижения tб.р до требуемой величины (см. формулы 10 и 11).
Пример 1. Завод должен изготовить и поставить в феврале-июле железобетонные преднапряженные оболочки диаметром 300 см, толщиной стенки 20 см, высотой 10 м, с обжатием бетона в продольном направлении усилием 75 кгс/cм2 и кольцевом - 65 кгс/см2. Оба торца не имеют заделки пробками. По технологическим условиям завода оболочки перед выдачей из камеры имеют наивысшую температуру бетона внутри стенки + 50°С.
Бетон оболочки имеет следующие характеристики:
γ = 2400 кг/м3, λ = 1,7 ккал/(м °С ч),
Е = 2100000 кгс/см2, σtдоп = 22,5 кгс/см2, Rиз = 0.
По данным ближайшей метеостанции за 5 лет, в течение февраля - июля возможны минимальная среднесуточная температуре воздуха - 25 °С и максимальная скорость ветра 23 м/с.
Требуется рассчитать максимальные растягивающие температурные напряжения σtmax в наружных слоях, возникающие от охлаждения при выдаче оболочек из камеры на открытую складскую площадку. По формуле (2) Δtp = 50-(-25) = 75°С.
По формуле (20) ![]()
При σminп.н = 65 кг/см2 по формуле (19)
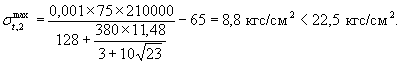
Следовательно, при выдаче оболочки из камеры на воздух с температурой -25°С и скоростью ветра 23 м/с опасность трещинообразования отсутствует.
Пример 2. Определить, можно ли выдавать оболочки на склад при тех же условиях, что и в примере 1.
По формуле (24)
![]()
Расчётная температура воздуха tв.p по формуле (10)
tв.p = 50 - 89,7 = -39,7°С, т.е. ниже -25°С.
Следовательно, оболочку можно выдавать непосредственно на склад.
2.2.3. В процессе пропитки горячими составами
Изложенная ниже методика относится к оболочкам преимущественно небольшого диаметра (30-60 см), которые для пропитки гидроизоляционными составами частично погружают (в вертикальном положении) в специальные ванны. Оба конца оболочки предварительно закрывают торцевыми заглушками.
Частичное погружение оболочки в ванну с горячим (с температурой до +180°С) составом сопровождается большими температурными перепадами по толщине стенки и по высоте (длине) оболочки. Возникающие при этом температурные напряжения могут вызвать появление трещин.
Напряжения σθ (кгс/см2)от перепада температуры по толщине стенки оболочки следует определять по формуле
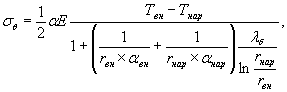 (25)
(25)
где Tв.н - максимальная температуре воздуха во внутренней полости оболочки, °С;
Тнар - минимальная температура воздуха, омывающего оболочку снаружи, °С;
rв.н - внутренний радиус оболочки, м;
αв.н - коэффициент теплообмена на внутренней поверхности оболочки, омываемой горячим воздухом, ккал/(м2 ч °С) Можно принимать αв.н = 50 ккал/м2 ч °С) в случаях пропитки составами с температурой 100-150°C;
rнар - наружный радиус оболочки, м;
αнар - коэффициент теплообмена на наружной поверхности оболочки, ккал/(м2 ч °С) При пропитке оболочки в ваннах на открытом воздухе принимается αнар = 20, а при пропитке в закрытом помещении αнар = 10;
λδ - коэффициент теплопроводности бетона оболочки, ккал/(м2 ч °С).
Напряжения σz (кгc/см2) от перепада температуры по высоте (длине) оболочки вблизи от поверхности пропитывающего состава следует определять по формуле
![]() (26)
(26)
где r - средний радиус оболочки, равный полусумме наружного и внутреннего радиусов, м;
hст - толщина стенки оболочки, м;
в - высоте участка опоры, на котором температура изменяется от температуры горячего состава до температуры окружающей среды, м. Обычно принимают в = 0,8-1 м;
ΔТ - перепад температуры по высоте (длине) оболочки, °С.
Если величина напряжений σθ и σz превосходит нормативное сопротивление бетона растяжению, то существует опасность появления трещин. Поэтому следует принимать меры по снижению температурных перепадов, например, ставить на крышку, покрывающую ванну с горячим составом, объемным кожух с диаметром в два раза больше диаметра оболочки и высотой 8-4 диаметра или устраивать съемную инвентарную теплоизоляцию из досок толщиной 3 см (или из материала, эквивалентного им по теплоизоляционным свойствам) на ту же высоту. Кожух представляет собой стакан, опрокинутый вверх дном, с отверстием в дне для пропуска оболочки.
Пример расчета. Рассчитать температурные напряжения, возникающие в опоре от перепадов температуры по высоте опоры и по толщине стенки при пропитке ее горячей смесью битума с петролатумом в закрытой помещении (αнар = 10 ккал/(м2 ч °С). Температура горячей смеси равна 130 °С, максимальная замеренная температура воздуха во внутренней полости опоры, нагретого от горячей смеси, Твн = 90°С, минимальная температура воздуха, омывающего опору снаружи, Тн = 6°С, Наружный радиус опоры rнар = 0,21 м, внутренний радиус rвн. = 0,155 м, средний радиус r = 0,1825 м, толщина стенки hст = 0,055 м. Марка бетона опоры 400; коэффициент линейного расширения α= 10-5 1/°С; модуль упругости бетона Е = 3,5×105 кгс/см2; нормативное сопротивление растяжению Rн = 25 кгc/cм2, коэффициент теплопроводности бетона λδ = 2 ккал/(м ч °С).
Делаются две проверки:
а) напряжения от перепада температур по высоте опоры по формуле (26), принимая в = 0,9 м и ΔТ = 130-5 = 125°С:
![]()
б) напряжения от перепада температур по толщине стенки по формуле (25), принимая αвн = 50 ккал/(м2 ч °С):
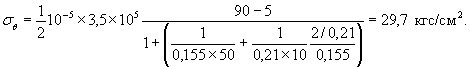
Во втором случае напряжения оказались выше нормативного сопротивления растяжению бетона, поэтому имеется опасность появления трещин. Для уменьшения напряжений можно, например, прикрыть разогретую смесь и участок опоры над ней объемным кожухом высотой 1-1,5 м. Температура воздуха под кожухом будет около 90°С. Тогда ΔТ = 130-90=40°С, а перепад температур по толщине исчезнет. Напряжения станут неопасными.
3. РАСЧЁТ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЙ В ЦИЛИНДРИЧЕСКИХ ОПОРАХ, ВОЗНИКАЮЩИХ В СТАДИИ ЭКСПЛУАТАЦИИ
3.1. Столбы сплошного сечения
3.1.1. В надводной зоне и над грунтом
В сечениях, удаленных вверх от горизонта воды и поверхности грунта более чем на два диаметра, в стадии эксплуатации температурные напряжения могут возникать при переходе от равномерного к невыгодному неравномерному распределению температур в опоре. Оно формируется под воздействием внешней среды, как правило, в холодный период года. Возникающие при этом напряжения суммируются с напряжениями, которые сохраняются в опоре после отвердевания бетона (см. п. 2.1.2). Суммарные напряжения от наиболее невыгодного неравномерного распределения температур по толщине опоры рассчитываются следующим образом.
Определяют расчетный перепад температуры по радиусу, который возможен в климатических условиях района расположения сооружения. С этой целью вначале для данного района по карте (приложение 2) определяют значение Ад - наибольшее понижение среднесуточной температуры воздуха за декаду. Затем по графику (рис. 3) для опоры данной толщины определяют перепад η, возникающий в опоре от декадного понижения температуры на 1°С. Умножая эту величину на расчётное значение Ад, получают расчётный перепад Т1 от декадного хода среднесуточной температуры воздуха.
При значениях коэффициента теплопроводности λg, отличающихся от величины 1,7 ккал/(м ч °С), соответствующие значения перепада η следует находить по графику на рис. 3 не для действительного диаметра опоры dg, а для фиктивного, определяемого по формуле
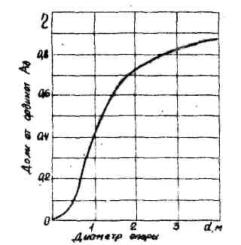
Рис. 3. График для определения перепада температуры между осью и поверхностью опоры от понижения на 1°С среднесуточной температуры воздуха за декаду
Температурные напряжения σθ (в кгс/см2), возникающие при переходе от равномерного к невыгодному неравномерному распределению температур в стадии эксплуатации, рассчитывают по формуле
где Н1* = 0,8 - коэффициент релаксации напряжений вследствие ползучести бетона;
α - коэффициент линейного температурного расширения, 1°C;
Е - модуль упругости бетона, кгс/см2;
ν - коэффициент Пуассона;
в - радиус опоры, cм;
r - расстояние от оси опоры до точки, в которой вычисляется напряжение, см (0 ≤ r ≤ в);
Т1 - расчётный перепад температуры по радиусу, °С (Т1=η×Ад).
Наконец, суммарные температурные напряжения в стадии эксплуатации определяют по формуле
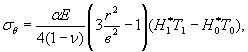 (29)
(29)
где H*0 и T0 - соответственно коэффициент релаксации и перепад температуры в период затвердения бетона, определяемые по данным, приведенным в п. 2.1.2.
Полученные напряжения сравнивают с нормативным и расчётным сопротивлениями бетона растяжению.
Пример расчёта. Требуется проверить трещиностойкость опоры моста в районе г. Минусинска. Диаметр опоры 300 см. Теплопроводность бетона λ = 1,7 ккал/(м ч °С); коэффициент линейного расширения α = 10-5 1/°С; модуль упругости бетона Е = 3,15×105 кгс/см2, коэффициент Пуассона ν = 0,15. Марка бетона 300.
Вначале по картам изолиний (см. приложение 2) определяют, что для района г. Минусинска значение Ад = 17°С, а по графику рис. 3 находят для заданного диаметра опоры соответствующее значение η = 0,84. Следовательно,
Т1 = η× Ад = 0,84×17 = 14,3°С,
Затем по формуле (28) рассчитывают распределение напряжений при переходе от равномерного к невыгодному неравномерному распределению температур. Например, на поверхности опоры (r = 150 см)
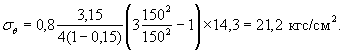
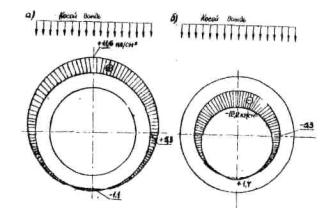
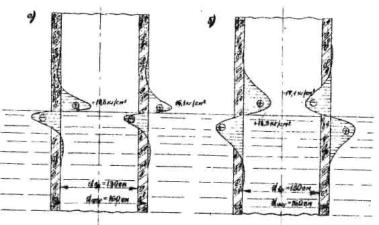
Аналогично вычисляются напряжения и в других точках по радиусу опоры. Соответствующая эпюра напряжений приведена на рис. 4, б, а на рис. 4, а, показана эпюра напряжений, возникающих в стадии строительства в той же опоре при выравнивании температур по диаметру после отвердевания бетона (см. п. 2.1.2 и пример расчёта там же).
Наконец, складывая алгебраически эпюры напряжений рис. 4, а и б или непосредственно по формуле (29), получаем эпюру суммарных напряжений, приведенную на рис. 4, в. Наибольшую величину растягивающие напряжения имеют на поверхности опоры и составляют 16 кгс/см2.
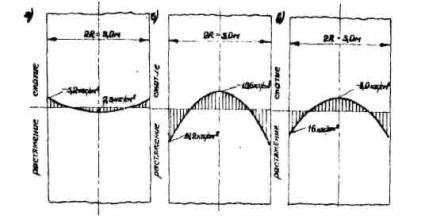
Рис. 4. Распределение тангенциальных напряжений:
а - при выравнивании температур по диаметру опоры после отвердевания бетона:
б - при переходе от равномерного к не выгоднейшему неравномерному распределению температур по диаметру;
в - суммарные напряжения
3.1.2. В уровне зимней межени при отсутствии льда
При длительном стоянии уровня воды в русловых цилиндрических опорах, кроме напряжений от перепадов температуры по толщине, возникают дополнительные температурные напряжения из-за перепадов температуры по высоте. Наибольшие растягивающие напряжения могут возникнуть в холодный период года в случае отсутствия льда на поверхности воды вследствие большего охлаждения части опоры, находящейся на воздухе, по сравнению с частью, находящейся в воде. Приведенная ниже методика расчёта напряжений справедлива для столбов диаметром-160-400 см.
Напряжения рассчитывают в два этапа.
На первом этапе определяют напряжения от неравномерности температуры по высоте опоры.
Вначале рассчитывают эффективный (с учётом ползучести бетона) перепад температуры Тр (в °С) надводной и подводной частей опоры:
Тр = 0,571 Тя+0,482 Ад,
где Тя - среднемесячная температура января (из табл.1 СНиП II-А.6-72 "Строительная климатология и геофизика"), но с противоположным знаком;
Ад - максимальное декадное понижение среднемесячных температур воздуха (см. приложение 2).
Затем рассчитывают распределение напряжений от неравномерности температуры по высоте. Исходными данными для этого расчёта служат напряжения от единичного перепада между подводной и надводной частями столба в трех точках по толщине в наиболее опасном надводном сечении (примерное расстояние от поверхности воды 0,12d где d - диаметр).
Напряжения принимают
на оси опоры - 0,71 кгс/(см3 °С);
на расстоянии 0,82 радиуса от оси - 0,56 кгс/(см2 °С);
на поверхности опоры - 0,36 кгс/(см2 °С).
Умножая эти данные на аффективный перепад Тр, получают распределение напряжений в трех точках по толщине опоры.
На втором этапе определяют суммарные напряжения с учётом напряжений от неравномерности температуры по толщине опоры.
Второй этап удобно выполнять графически, т.е. получать суммарное распределение напряжений, складывая эпюру, построенную на первом этапе, с второй, полученной по методике, изложенной в п. 3.1.1.
Пример расчёта. Определим температурные напряжения в цилиндрической железобетонной опоре диаметром 300 см, установленной в русловой части моста, который расположен в районе г. Минусинска. Среднемесячная температуре января Тя = -21,2°С, максимальное декадное похолодание Ад = 17°С. Марка бетона 300.
Первый этап. Определяем эффективный перепад температуры между подводной и надводной частями столба:
Тр = 0,571-21,2+0,482×17 = 20,3°С.
Затем рассчитываем распределение напряжений по толщине от неравномерности температуры по высоте опоры. На расстоянии 0,82 радиуса от оси (т.е. для r = 0,82×1,5 = 1,23 м) σθh = 0,56×20,3 = 11,4 кгс/см2.
Аналогично определяется этот вид напряжений для оси цилиндра и его поверхности. Затем по трем точкам строят распределение напряжений по толщине, что показано на рис. 5, б.
На рис. 5, а приведена эпюра напряжений от неравномерности температур по радиусу (см. п. 3.1.1. и пример расчета там же).
второй этап. Суммарное распределение напряжений (рис. 5, в) получают, складывая эпюры а и б на рис. 5.
Анализируя суммарную эпюру напряжений, можно видеть, что суммарные тангенциальные напряжения могут превосходить не только расчётное, но и нормативное сопротивление бетона растяжению, которое для бетона марки 300 составляет 21 кгс/см2.
На основании этого расчёта можно утверждать, что над поверхностью воды в опоре возможно образование продольных трещин.
3.1.3. В зоне переменного горизонта воды (п.г.в.)
При проектировании, столбчатых опор для каждого конкретного пункта строительства должны рассчитываться максимальные растягивающие температурные напряжения, σtmax возникающие в периферийных слоях столбов после резкого понижения уровня воды около них в холодное время года.
Расчет σtmax (в кгс/см2) должен производиться по формулам:
а) в случае отсутствия теплоизоляции на поверхности столбов
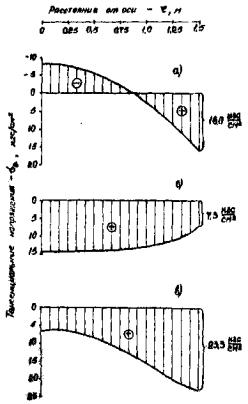
Рис. 5. Распределение тангенциальных напряжений по радиусу опоры в опасном сечении (0,36 м над поверхностью воды):
а - от неравномерности температур по радиусу; б - от неравномерности температур по высоте; в - суммарные
б) при наличии теплоизоляции
где Δtp=t1-t2 - наибольший перепад температур между водой и воздухом, возникающий в холодный период года;
t1 - температуре воды (можно принять °С);
t2 - средняя температура воздуха в наиболее холодные сутки;
β - коэффициент, учитывающий геометрическую форму опор: для опор без ребер (круглое очертание) β = 380 (для опор с ребрами (многогранник) β = 132;
Мпр - расчетный модуль поверхности, м-1;
Vmax - максимальная скорость ветра, м/с, возможная один раз за 5 лет;
Для сплошного цилиндра
Для опоры восьмиугольного сечения
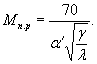 (33)
(33)
где α' - ширина грани, м.
Для обеспечения трещиностойкости и долговечности опор в зоне переменного горизонта воды значение рассчитанных σtmax не должно превышать предельной величины Rр (в кгс/см2), определяемой по формуле
Rp = (RH-σq)×n, (34)
где RH - нормативный предел прочности бетона на растяжение, кгс/см2
σq - растягивающие напряжения в поверхностном слое опор от внешней нагрузки, кгс/см2
n - коэффициент, учитывающий особенности температурных воздействий (n = 1 для опор, защищенных теплоизоляцией с гидроизоляционными свойствами, n = 0,5 для опор, защищенных теплоизоляцией, не обладающей гидроизоляционными свойствам).
Для снижения σtmax до Rp необходимо устраивать на поверхности опор гидротеплоизоляцию - облицовку с термическим сопротивление Rиз (в м2 °С ч/ккал), определяемым по формулам:
а) для сплошных цилиндрических опор:
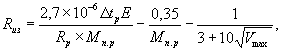 (35)
(35)
б) для опор с ребрами (многоугольных)
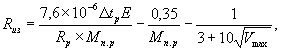 (36)
(36)
Толщину теплоизоляции - облицовки lo (в м) из запроектированного материала определяют по формуле
lo = Rиз×λm, (37)
где λm - коэффициент теплопроводности теплоизоляции - облицовки, ккал/(м °С ч).
Пример. Опора моста из железобетонных столбов сплошного сечения диаметром 60 см строится в районе г. Минусинска. Требуется проверить величину максимальных растягивающих напряжений в поверхностных слоях в зоне переменного горизонта воды.
Характеристики бетона λ = 1,7 ккал/(м.°С ч), γ = 2500 кг/м3, Е = 210000 кгс/см2, Rн = 22,5 кгc/см2 σq = 0.
В г. Минусинске Vmax = 23 м/с, t1 = 0°С, t2 = 48°С, Δtp = 0 - (-43) = 43°С.
По формуле (34)
Rр = (22,5-0)×0,5 = 11,3 кг/см2.
Величина Мп.р определяется по формуле (32)
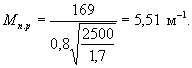
Величина σtmax для сваи без теплоизоляции рассчитывается по формуле (30)
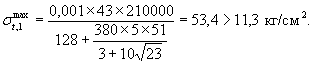
Для снижения σt,1max = 53,4 кг/cм2 до Rр = 11,3 кг/см2 применим теплоизоляцию - облицовку без гидроизоляционных своств с термическим сопротивлением Rиз, определяемым по формуле (35)
![]()
После устройства теплоизоляции - облицовки с Rиз = 0,31 м2 °С ч/ккал величина σt,2max формуле (31) равна
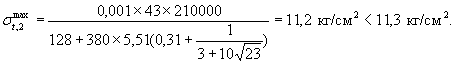
Для теплоизоляции - облицовки используем керамзитобетон с λ = 0,20 ккал/(м·°С ч), защищенный снаружи от ледохода металлическим листом толщиной 1 см. Тогда толщина теплоизоляции - облицовки по формуле (37) равна
l0 = 0,3×10,2 = 0,062, или 6,2 см.
3.1.4. В пределах наледи
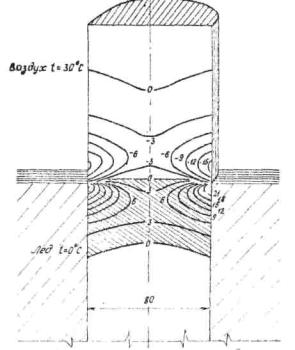
Образование наледи вокруг столбчатой опоры вызывает возникновение неравномерных температурных полей в бетоне со значительными перепадами температуры как по толщине столба, так и по высоте. По радиусу столба самое невыгодное распределение температуры возникает из-за более быстрого охлаждения поверхностных слоев, а по высоте - из-за большего охлаждения зимой или нагрева летом части столба, находящейся в наледи.
Чтобы оценить трещиностойкость столба в пределах наледи и запроектировать мероприятия по защите бетона, строят осесимметричное поле тангенциальных температурных напряжений. Для построения поля вначале рассчитывают напряжения в 50 характерных точках по одну сторону от оси столба с координатами:
по радиусу (отсчет ведется от оси столба) 0; 0,3r; 0,6r; 0,9r; r;
по высоте (отсчет вверх и вниз от поверхности наледи) ±0,1r; ±0,4r; ±0,8r; ±1,2r; ±1,7r.
В табл. 1 для точек с этими
координатами даны тангенциальные температурные напряжения от единичной
температурной нагрузки двух видов: длительной и кратковременной. В качестве
основной характеристики длительной температурной нагрузки принята
среднемесячная температура воздуха (в январе). В качества основной
характеристики кратковременной температурной нагрузки принято декадное
понижение. Амплитуду декадного понижения отыскивают по карте изолиний (см. приложение 2).
Значения напряжений от единичной температурной нагрузки, взятые из табл. 1,
умножают на величину соответствующей фактической температурной нагрузки. К
полученным величинам делают следующие поправки. Ориентировочно учитывают
ползучесть с помощью понижающих коэффициентов: 0,75 - для длительной
температурной нагрузки и 0,85 - для кратковременной. Учитывают фактические
значения коэффициента температурного линейного расширения бетона α и модуля
упругости Е путем умножения полученных величин напряжений на отношение ![]() . После этого строят осесимметричное поле (в виде изолиний, проведенных
через 2-5 кгс/см) тангенциальных температурных напряжений, сравнивают
напряжения в наиболее опасных местах с расчетными и нормативными для бетона, из
которого изготовлен столб, и делают выводы о необходимости применения тех или
иных мероприятий по защите бетона от разрушения.
. После этого строят осесимметричное поле (в виде изолиний, проведенных
через 2-5 кгс/см) тангенциальных температурных напряжений, сравнивают
напряжения в наиболее опасных местах с расчетными и нормативными для бетона, из
которого изготовлен столб, и делают выводы о необходимости применения тех или
иных мероприятий по защите бетона от разрушения.
Следует выполнять проверку для трех расчётных случаев: двух в зимний период (длительная и кратковременная нагрузка) и одного в весенне-летний (только длительная). Для третьего расчетного случая, в которой температура верхней части столба выше температуры нижней, знаки единичных напряжений из табл. 1 необходимо поменять на обратные.