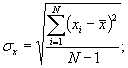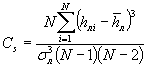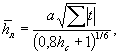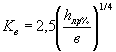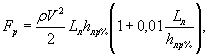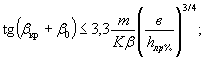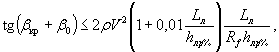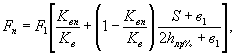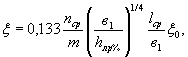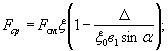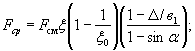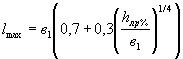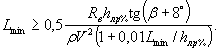"Методические указания" составлены на основании разработанной методики, позволяющей более обосновано определять ледовые нагрузки на опоры мостов за счет ряда существенных коррективов к требованиям действующих нормативных документов. Эти коррективы относятся как к определению ледовых нагрузок, так и назначению расчетных прочностных характеристик льда.

На основании результатов теоретических и экспериментальных исследований с использованием заменителя льда (эквивалентным материалом) и известных методов строительной механики уточнены методы расчета ледовых нагрузок на опоры в широком диапазоне их конструктивных особенностей (в частности, для опор безростверкового типа), ситуационных условий (например, косое направление воздействия ледяных полей) и др.

Сравнение фактических прочностных характеристик льда к периоду первой подвижки для участков сибирских и дальневосточных рек с рекомендуемыми в нормативных документах подтверждает о значительных запасах, заложенных в последних при определении ледовых воздействий. Эти запасы связаны с тем, что, во-первых, нормы не учитывают уменьшение прочности ледяного покрова от начала его таяния до первых подвижек, когда прочность льда снижается под влиянием поглощаемого тепла солнечной радиации. Во-вторых, тепловой баланс тающего ледяного покрова включает в себя комплекс климатических и метеорологических факторов (высоты снежного покрова, облачность и т.п.). Поэтому принцип изменения расчетной прочности льда с увеличением географической, широты местности (от 1,2 до двух раз), заложенный в нормы, не соответствует действительности.

На основе большого статистического материала о поступлении солнечной радиации на землю в весенний период в различных регионах России в работе приведена карта районирования по зонам коэффициента снижения прочности льда по сравнение с нормативной, т.е. с учетом реальных климатических условий, определяющих прочность льда на реках перед ледоходом.

Настоящие указания предназначается для использования по согласованию с заказчиком до переработки действующих СНиП 2.05.03-84*, которые устарели в части требований к расчетным гидрологическим параметрам и, в частности, определение ледовых воздействий на опоры мостов.

Указания разработаны в творческом коллективе (ТК) «ГИДРАВЛИК» АО «ЦНИИС» докт. техн. наук А.Н. Милитеевым и канд. техн. наук В.Ш. Цыпиным при творческом участии докт. геогр. наук Б.М. Гинзбурга, канд. геогр. наук СВ. Борща, К.Н. Поляковой, М.Б. Пономарева (РосГидрометцентр) и канд. техн. наук В.П. Афанасьева (ЛИИЖТ).

Авторы выражают благодарность инж. Л.Н. Подольцеву (Специализированная фирма "Мостострой") за конструктивную критику и полезные советы.

I. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Настоящие Методические указания предназначены для использования при проектировании железнодорожных и автодорожных мостовых переходов через реки на территории России и включают методику определения нагрузки от ледяных полей ^х) на промежуточные опоры мостов.

_____________________

^х) Под принятым в нормативных документах термином "ледяные поля" следует понимать отделившиеся участки ледяного покрова, отличающиеся от отдельных льдин своими большими размерами. Правомерно (особенно для конкретных объектов и периода ледохода) ледяное поле называть также льдиной.

1.2. Составлению проектов мостовых переходов через большие и средние реки должны предшествовать изыскания, в результате которых наряду с топографией, инженерно- геологическими условиями района перехода, гидрологическим режимом и русловым процессом пересекаемого водотока, необходимо изучение ледовой обстановки в районе перехода.

До начала полевых изыскательских работ производят сбор и изучение материалов о режиме (в том числе ледовом) пересекаемой реки в районе перехода с целью выявления недостающих материалов и составления более полной, программы полевого обследования ледовой обстановки.

В результате подготовительных, полевых и камеральных работ должны быть получены необходимые данные для определения расчетных (наиболее неблагоприятных) ледовых воздействий на сооружения перехода. Эти данные должны включать:

уровни (место приложения нагрузки) в различные периоды очищения реки ото льда;

геометрические размеры ледовых образований и скорость их перемещения;

механические свойства (прочность) льда в периоды его воздействия на сооружения;

размеры и ледотермический режим водоема, определяющие возможный тип ледовой нагрузки и воздействий на сооружения.

1.3. На стадии подготовительных работ необходимо выявить опорные пункты для определения гидрологических, климатических и непосредственно ледовых условий в районе перехода.

В качестве таких пунктов могут быть приняты водомерные посты и метеорологические станции Росгидромет службы или пункты других ведомств, на которых ведутся соответствующие наблюдения и удовлетворяющие следующим условиям:

расположение не далее чем на 100 км южнее, на 200 км западнее или восточнее и на 300 км севернее от створа мостового перехода;

находятся в близких для проектируемого мостового перехода гидроморфологических, ситуационных и антропогенных условиях;

наблюдения за характеристиками льда ведутся на той же реке, через которую

проектируют мост,

Если опорные пункты расположены выше и ниже по течению реки, то при прочих примерно равных условиях (включая и период наблюдений) рекомендуется использовать данные вышележащих постов.

1.4. На опорных пунктах определяют:

даты ранней и поздней первой подвижки льда; раннего, позднего и высокого весеннего и осеннего ледохода;

максимальные толщины льда в зимний период за все годы наблюдений;

среднюю (в зимний период) толщину снега на льду за годы наблюдений;

среднесуточную температуру воздуха в каждые сутки за период от ледостава до начала ледохода;

подекадную (понедельную или полумесячную) среднюю скорость ветра в период ледостава, наибольшую - в период ледохода.

1.5. Программа полевого обследования ледовой остановки должна предусматривать выполнение комплекса работ, включающего, выявления:

максимальных и минимальных уровней первой подвижки льда; максимальных уровней весеннего (и осеннего) ледохода; места образования заторов и зажоров льда, причины их возникновения, уровни и отметки наибольших заторов и зажоров; места выхода льда на пойму, навалов льда на берега и образования постоянных полыней;

случаи разрушения берегов и сооружений ледоходом и при прорыве заторов; расчетные размеры ледовых полей и льдин, толщину льда;

густоту, скорость и направления движения льдин на участке мостового перехода.

1.6. Состав и объем полевых работ определяют, исходя из ледового режима реки и степени его изученности, сроков разработки проектной документации и стадии проектирования.

По требованиям СНиП 2.05.03-84 /3/ исходные данные по ледовой обстановке необходимо устанавливать по ряду натурных наблюдений не менее 5 лет. Независимо от сроков наблюдений используют материалы Ресурсов поверхностных вод, Государственного кадастра, проектные и изыскательские материалы организаций, проводивших работы на исследуемом объекте ранее.

Методику и объемы работ, включая их камеральную обработку, устанавливают с учетом рекомендаций Пособия /1/ и Наставления /2/.

1.7. В настоящее время ведутся уточнения действующих нормативных документов для проектирования мостовых переходов в части назначения расчетных вероятностей уровней (паводков) и толщины льда на основе учета климатических особенностей региона и минимизации строительно-эксплуатационных затрат.

До утверждения новых норм, предлагаемые расчетные вероятности паводков (табл. 1.1-1.2) и толщин льда носят рекомендательный характер. Вероятности паводков дифференцируются в зависимости от категории дорог и региона на территории России, характеризуемого зонами водоопасности (рис. 1.1). В предлагаемых нормах расчетную вероятность толщины льда следует принимать для всех категорий дорог равной 1% при коэффициенте асимметрии изменения ежегодных максимумов толщин льда C_s > 0,5 и 2% при C_s < 0,5 (см. рис. 2.1).

Рекомендуемые расчетные вероятности паводков (в %) для мостовых переходов на автомобильных дорогах.

Таблица 1.1.

Категория дорог	Зоны водоопасности
Категория дорог	Малая (I)	Средняя (II)	Повышенная (III)	Большая (IV)	Наибольшая (V)
I	2,5	1,0	0,4	0,33	0,25
II	2,5	1,0	0,5	0,33	0,25
HI	3,0	1,0	0,5	0,4	0,25
IV	3,0	1,0	0,67	0,4	0,33
V	4,0	1,5	0,8	0,5	0,4

Рекомендуемые расчетные вероятности паводков (в %) для мостовых переходов на железных дорогах

Таблица 1.2.

Категория линий	Зоны водоопасности
Категория линий	Малая (I)	Средняя (И)	Повышенная (III)	Большая (IV)	Наибольшая (V)
I-II	2,0	0,67	0,33	0,25	0,20
III	2,5	1,0	0,40	0,33	0,25
IV	4,0	1,5	1,0	0,67	0,5

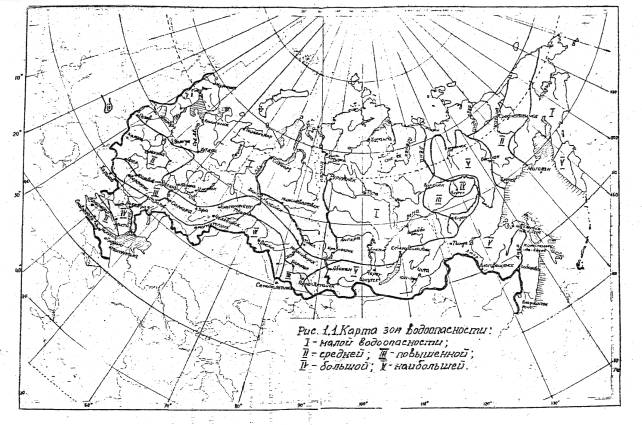
Рис 1.1. Карта зон водоопасности:

I - малой водоопасности; II - средней; III - повышенной; IV - большой; V - наибольшей.

1.8. При определении ледовой нагрузки на опоры мостов рассматривается случай остановки сооружением (с последующем разрушением) ледяного поля перемещающегося под действием течения, ветра или подъема уровня в период первой подвижки льда и ледохода.

Наибольшие воздействия льда на опоры происходят при первых подвижках, т.е. небольших перемещениях ледяного покрова непосредственно перед вскрытием реки (водохранилища).

В период ледохода прочность льда (за счет повышения его температуры до 0°С) минимально возможная; но приложение ледовой нагрузки существенно изменяться и определяется подъемом уровня воды.

1.9. В расчетах все физико-механические (прочностные) характеристики льда принимаются как осредненные по его толщине.

В расчетных формулах следует принимать, если особо не оговаривается, линейные размеры в метрах, нормативные сопротивления (прочность) льда в МПа (1 МПа » 100 тс/м) и получать величину нагрузок на опоры мостов в МН (1 МН » 100 т.с).

Приведенные зависимости по учету косого направления воздействия ледяных полей на опоры мостов справедливы при угле между продольной осью опоры и вектором силы до 30°.

2. ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ ИСХОДНЫХ ДАННЫХ ПО ЛЕДОВОЙ ОБСТАНОВКЕ В РАЙОНЕ ПЕРЕХОДА.

2.1. Методы определения расчетных исходных данных по ледовой обстановке зависят от продолжительности периода наблюдений за изучаемым параметром и подразделяются на три группы, характеризуемые: наличием, недостаточностью и отсутствием данных наблюдений.

2.2. К первой группе (наличие данных) наблюдений относятся периоды, которые являются репрезентативными (представительными), а величина относительной среднеквадратической ошибки ξ_х расчетного значения исследуемой характеристики не превышает 10 % /4/.

Наблюдения на створе перехода или расчетных опорных пунктах удовлетворяют указанные условия (репрезентативные) при продолжительности периода не менее:

15 лет для определения толщины льда;

20 лет для уровней льда и воды, когда водоток не освобожден ото льда;

25 лет для скорости ветра и уровней воды в безледные сезоны /3/.

При меньшей продолжительности периода к первой группе относятся наблюдения, если

(2.1)

где σ_х - среднее квадратическое отклонение от средней величины рассматриваемого параметра при периоде наблюдения N лет

(2.2)

x_i - величина рассматриваемого параметра в i-ом году.

Среднюю (или среднюю многолетнюю) величину определяют как среднее арифметическое по формуле

(2.3)

где - сумма величин, из которых составлен ряд из N членов.

2.3. Ко второй группе (недостаточных данных) относятся наблюдения, которые не могут быть отнесены к первой группе (см. п. 2.2) при продолжительности периода не менее: 5 лет для толщины льда /5/; 10 лет для уровней воды /4/ и скоростей ветра.

Все остальные случаи следует рассматривать как отсутствие данных наблюдений.

ОПРЕДЕЛЕНИЕ ТОЛЩИНЫ ЛЬДА.

2.4. Толщину льда за зимний период расчетной вероятности р_л определяют по формуле

(2.4)

где - средняя из ежегодных максимумов за зимний период толщина льда;

σ_л - среднеквадратическое отклонение ежегодных максимумов толщин льда за зимний период от ;

Ф_р_% - отклонение ординаты привой вероятностей Пирсона III типа от середины (Приложение 1) для расчетной вероятности толщины льда р_л и коэффициента асимметрии C_s ежегодных максимумов толщин льда.

Методы определения величин , σ_л и C_s зависят от продолжительности периода наблюдений за толщиной льда.

2.5. При наличии данных наблюдений среднюю из ежегодных максимумов за зимний период толщину льда и среднеквадратическое отклонение толщин льда σ_л определяют соответственно по формулам (2.3) и (2.2), а коэффициент асимметрии C_s ежегодных максимумов толщин льда по формуле

(2.5)

2.6. При отсутствии данных наблюдений параметры σ_л и C_s принимают по карте (рис. 2.1), а среднюю, толщину льда по формуле (в см)

(2.6)

где а - коэффициент, принимаемый равным 1,7 для рек в Европейской части России южнее широты 65° и в Азиатской части южнее широты 55° севернее указанных районов а = 2,4;

Σ|t| - средняя за период не менее 15 лет сумма отрицательных среднесуточных температур воздуха (в градусах Цельсия) от ледостава до начала снеготаяния по данный опорных метеостанцией;

h_c - средняя за зимний период высота (в м) снежного покрова, определяемая по показаниям метеостанции.

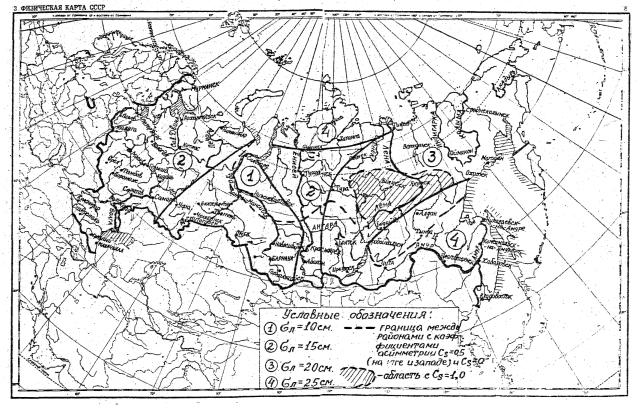
Рис. 2.1. Карта зон одинаковых среднеквадратических отклонений ежегодных максимумов толщин льда σ_л

При расчете средней толщины льда по формуле (2.6) следует учитывать особенности формирования ледового покрова.

При прочих равных условиях: заболоченность рек уменьшает на 10-15 см толщину льда, образуемого за зимний период;

на участках с осенними заторами и зажорами, а также в районах, характеризующихся осенним ледоходом, из-за образования ледяного покрова сразу из более толстого и торосистого льда толщина его может быть увеличена до 30 см.

2.7. При недостаточных данных наблюдений (при N ≥ 5 лет) среднюю толщину льда можно определять двумя способами: с использованием эмпирической формулы (2.6) и статистическим методом.

Первый способ сводится к уточнению значения в формуле (2.6) по средней сумме отрицательных среднесуточных температур за N лет наблюдений и средней толщине льда 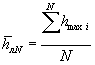за тот же период. Искомый средний параметр определяется как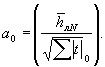

По второму способу наибольшая толщина льда за N лет наблюдений h_maxN принимают обеспеченностью 1 раз в N лет (или вероятностью 1/N). Тогда из формулы (2.4)

(2.7)

где Ф_1/N - отклонение ординаты кривой вероятностей Пирсона III типа от середины для вероятности 1/N (см. Приложение 1);

σ_л_N = σ_лγ - среднеквадратическое отклонение толщин льда при малом числе ряда (N < 15);

γ - коэффициент уменьшения σ_л доверительной вероятностно 0,9, который принимают равным (для χ² - распределения);

N ...	5	68	10	12	15
γ ...	0,65	0,68	0,72	0,76

К расчету рекомендуется принимать большее значение средней толщины льда h_л, полученное по двум способам.

2.8. За расчетную толщину льда h_лр_% следует принимать толщину льда расчетной вероятности на период его первой подвижки

h_лр_% = α h_maxр%, (2.8)

где α - коэффициент уменьшения к моменту первой подвижки максимальной толщины льда за зимний период h_maxр% той же расчетной вероятности (см. п. 2.4), который по действующим нормативным документам /3, 5/ требуется принимать равным 0,8. На основании натурных обследований возможна следующая дифференциация значений коэффициента α:

0,7 - для бассейна р. Амура вниз по течению до г. Хабаровска включительно;

0,9 - регион севернее линии Смоленск-Волгоград и южнее линии С. Петербург - Москва - Казань - Магнитогорск; верховье бассейна р. Обь до Новосибирска; бассейн рек Енисея севернее притона Ангары и Лены севернее г. Якутска;

0,8 - остальная территория России.

Указанные регионы относятся соответственно к зонам №№ 1, 4 и 2-3 на рис. 3.3.

ОПРЕДЕЛЕНИЕ ХАРАКТЕРНЫХ УРОВНЕЙ.

2.9. В качестве максимальных уровней весеннего (и осеннего) ледохода принимают уровни высшего наблюденного (старожилами) ледохода (УВНЛ). Эти уровни служат качественной оценкой при нахождении уровня высокого ледохода расчетной вероятности. (РУВЛ_р_%) которую назначают равной расчетной вероятности паводка р для проектируемого мостового перехода.

РУВЛ_р_% определяют теми же методами, как расчетные уровни паводков /1, 4/. При отсутствии данных многолетних наблюдений для бассейнов средних и нижних течений крупных рек Сибири и Европейского Севера России уровни высокого ледохода можно принимать совпадающими с наивысшими уровнями весенних половодий. Для остальных регионов России уровни высокого ледохода можно определять по приближенной зависимости

Q_влp% = KQ_1%, (2.9)

где Q_влp% - расход воды, наивысший уровень которого соответствует уровню ледохода вероятностью р;

Q_1% - максимальный (пиковый) расход воды весеннего половодья вероятностью р = 1%:

K - коэффициент, определяемый по формуле (вероятности р принимают в %)

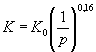(2.10)

В формуле (2.10) K₀ = 0,59.

Уровни (Н) снимают с морфометрической кривой Q =f(Н).

При отсутствии гидрологических наблюдений на участках заторообразования подъем заторного уровня над уровнем ледохода можно определять по формуле

Н_зат = (22i^0,3 - 1)Н_л, (2.11)

где Н_л, i глубина и уклон (в долях единицы) потока в русле при ледоходе.

2.10. В качестве максимальных и минимальных уровней первой подвижки льда принимают уровни ледостава (Ул_р%) вероятностью, соответственно 1 % и 99 %.

При наличии наблюдений уровни первой подвижки указанной вероятности (обеспеченности) рассчитывают путем обработки соответствующего ряда уровней ледостава известным в гидрологии статистическим способом /1/.

В регионах, где преобладает сток весеннего половодья, в качестве уровней подвижки льда можно принимать уровни низкой межени (УНМ) той же обеспеченности.

При отсутствии данных многолетних наблюдений минимальный уровень первой подвижки льда можно, принимать, по формуле:

Q_пл = KQ_1%, (2.12)

где Q_пл расход воды, соответствующей минимальному уровню первой подвижки льда;

Q_1% - см. формулу (2.9);

K - см. формулу (2.10), в которой K₀ = 0,24.

РАСЧЕТНЫЕ СКОРОСТИ ТЕЧЕНИЯ, ДВИЖЕНИЯ ЛЕДЯНЫХ ПОЛЕЙ И ВЕТРА ПРИ ОПРЕДЕЛЕНИИ НАГРУЗКИ ОТ ЛЕДЯНОГО ПОЛЯ.

2.11. Для рек в качестве расчетных "скорости движения ледяных полей" V и «максимальной скорости течения воды подо льдом 1%-ой обеспеченности в период ледохода» V_max требуемые СНиП 2.06.04-82* для определения воздействий на сооружения от движущихся и остановившихся ледяных полей, следует принимать (при отсутствии натурных наблюдений) среднюю для русла поверхностную скорость течения воды при расчетном уровне высокого ледохода (РУВЛ_р_%).

Эта расчетная скорость V_pacч. = V = V_max для практических расчетов может определяться как V_pacч. = 1,25 V_cp, где V_cp - средняя скорость течения воды в русле при РУВЛ_р_%.

2.12. Для водохранилищ расчетную, скорость движения ледяных полей следует принимать (при отсутствии натурных наблюдений) равной

V_max = 0,03 V_Wmax,

где V_Wmax - скорость ветра 1%-ной обеспеченности в период движения льда (т.е. период от ранней даты начала первой подвижки до поздней даты освобождения ото льда части водохранилища со стороны верхнего бьефа моста).

2.13. При определении воздействий на сооружения от остановившегося ледяного поля в качестве "максимальной скорости ветра в период ледохода 1%-ной обеспеченности" /3/ V_Wmax следует принимать скорость ветра 1%-ой обеспеченности в период от самой ранней даты начала до самой поздней даты конца ледохода.

Эту скорость, а также скорость ветра на водохранилищах (см. п. 2.12) определяют по данным опорных метеостанцией статистическим методом, для совокупности опасных направлений, которые для рек совпадают с направлением течения, а для водохранилищ - за исключением параллельных оси моста.

Для практических расчетов скоростей ветра в период наблюдений включают полные месяцы, в которых началось и закончилось очищения водотока ото льда. Например, при самой ранней дате начала ледохода 17 апреля и самой поздней даты его конца 12 июня в расчет принимают три полных месяца: апрель, май, июнь.

Порядок статистической обработки данных опорной метеостанции, приведенных к водной поверхности у мостового перехода, изложен в Пособии /1/.

2.14. Данные о размерах ледяных полей во время ледохода устанавливают опросом местных жителей, "по натурным наблюдениям в данном или смежных пунктах" или назначают:

длину L_л = 0,1 В_р, где В_р - ширина реки во время вскрытия льда;

площадь А = L_л L_m, где L_m - средняя длина ледяного поля по направлению потока (или ветра), равная L_m = 3 В_р, а для водохранилищ L_m » 30 L_л.

При этом в расчетах следует принимать ширину ледяного поля L_л не более наибольшего пролета, опирающегося на рассматриваемую опору, а длину L_m - не больше расстояния вверх по течению до вершины ближайшей излучину с углом разворота свыше 60 или длины разгона по направлению расчетного ветра.

3. ПРОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ЛЬДА.

3.1. Для расчетов нагрузок на опоры мостов используются нормативные сопротивления (или пределы прочности) льда сжатию R_c, изгибу R_f, смятию R_в и срезу R_cp.

По действующим нормативным документам /3, 5/ рекомендуется прочностные характеристики льда определять "по опытным данным", хотя практически это выполнить нельзя из-за невозможности хранения и транспортировки образцов, громоздкости и маломобильности оборудования для испытаний разрушающими методами, отсутствия приборов для получения прочностных характеристик неразрушающими методами и т.п.

В связи с отсутствием опытных данных "допускается принимать" приводимые в нормативных документах значения нормативных сопротивлений льда, полученных на основании массовых испытаний образцов при температуре льда в диапазоне от 0°С до -30°С.

3.2. По нормам в качестве температуры пресного" льда следует принимать среднюю температуру воздуха трехсуточного периода, предшествующего действию льда на сооружение при толщине льда 0,5 м и менее, и за шестисуточный период при толщине льда более 0,5 м.

____________________

^х В настоящих Методических указаниях рекомендации составлены для пресноводного льда.

Для практических расчетов необходимо определить температуру льда при первой его подвижке t_ap. С этой цель требуется по данным опорных водомерного поста и метеостанции получить не менее чем за N = 15 лет даты первой подвижки льда и предшествующие этому явлению среднесуточные (соответственно за трое или шестеро суток) температуры воздуха t_ai в те же годы. Тогда расчетная температура льда определяется как .

При отсутствии на водпосту данных о начале первой подвижки дату первой подвижки можно принимать для территории России ориентировочно по карте (рис. 3.1).

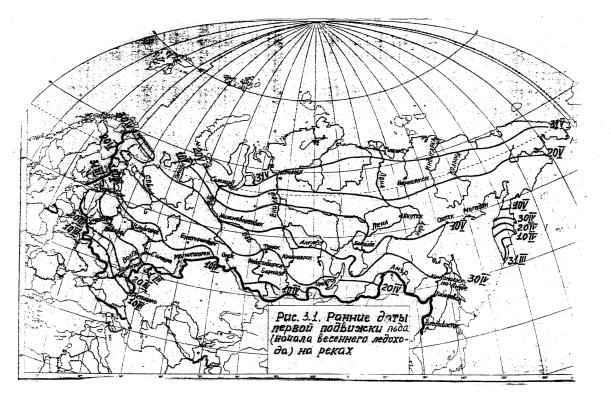
Рис. 3.1. Ранние даты первой подвижки льда (начало весеннего ледохода) на реках

Для предварительных расчетов согласно рекомендациям СНиП 2.05.03-84 температуру льда на период первой подвижки можно приникать равной -3°С.

Температуру льда при ледоходе следует принимать равной 0°С.

3.3. Прочность льда на реках и водохранилищах к началу его движения (подвижек) и при ледоходе под влиянием поглощаемого льдом тепла солнечной радиации может оказаться существенно меньше прочности эталонных образцов, получение при той же температуре в морозильных камерах. Это явление давно известно гидрохимикам и теоретически обосновано еще в 70-х годах С.Н. Булатовым.

С учетом реальных условий поглощения льдом тепла солнечной радиации расчетную прочность льда перед его первой подвижкой следует определять по формуле:

R_i = φR_i^H, (3.1)

где φ - коэффициент снижения прочности льда под влиянием солнечной радиации у сооружений (см. п. 3.8) по сравнению с нормативным сопротивлением льда R_i^H при той же температуре. Под нормативным сопротивлением льда (в отличие от его расчетной прочности) далее будет пониматься прочность при испытании эталонных образцов. Индекс «i» характеризует вид прочности льда (на сжатие, изгиб, смятие, срез).

3.4. Нормативное сопротивление при испытании эталонных образцов на одноосное сжатие R_c^H, в зависимости от температуры льда t_a, °C, рекомендуется принимать по СНиП 2.06.04-82*.

t_a, °C ...	0	-3	≤-3
R_c^H, МПа ...	0,44	0,75	0,54 \|t_а\|^0,3

3.5. Нормативное сопротивление льда изгибу R_f^H следует определять по формуле

R_f^H = 0,75R_c^H (3.2)

3.6. Нормативное сопротивление льда R_в^H следует определять по формуле:

R_в^H = K_в R_c^H (3.3)

где K_в - коэффициент, зависящий от относительной ширины сооружения в/h_л_p_% и определяемый согласно СНиП 2.06.04-82* по формуле

(3.4)

При

За ширину сооружения следует принимать расстояние между крайними частями опоры по фронту на уровне действия льда (рис. 3.2) в случаях:

а) если по указанному фронту опора сплошная (без просветов);

б) если опора состоит из ряда элементов (свай, столбов и т.п.), между которыми имеются просветы S ≤ 2h_л_p_%.

При элементы опоры не взаимодействуют между собой, и коэффициент K_в следует определять отдельно для каждого элемента шириной в₁.

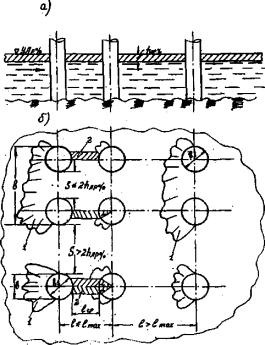
Рис. 3.2. Характер разрушения ледяного покрова в зависимости от расположения элементов опор относительно друг друга:

а, б - профиль и план ряда из столбов диаметром в₁; 1 - скол (смятие) льда; 2 - срез льда между столбами

3.7. Нормативное сопротивление льда срезу можно определять по данным К.Н. Коржавина как

R_cp^H=1/3R_c^H (3.5)

3.8. Коэффициент снижения прочности льда под влиянием солнечной радиации (φ зависит от климатических особенностей региона, где расположен мостовой, переход. По степени снижения относительной прочности ледяного покрова (φ = R_i/R_i^H) к моменту вскрытия водотоков территория России разделена на 4 зоны (рис. 3.3).

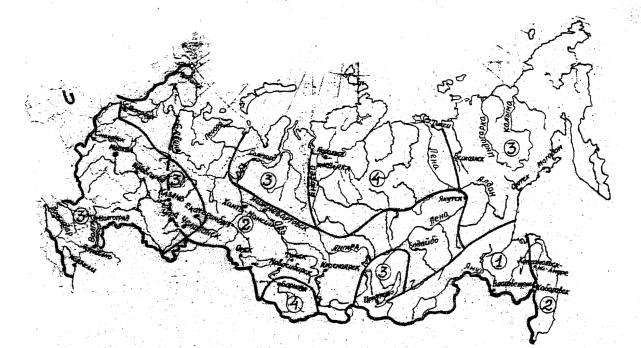
Рис. 3.3. Карта районирования по зонам коэффициента φ снижения прочности льда под влиянием солнечной

радиации.

- граница и номера зон

- граница допускаемого снижения прочности льда по СНиП 2.06.04-82*

Каждая зона характеризуется одинаковым средним значением коэффициента φ, который определяется комплексом независимых случайных явлений и процессов (толщина снежного покрова облачность, наличие ветра и т.п.). Вероятность сочетания неблагоприятных явлений к периоду подвижки льда (т.е. меньшего воздействия солнечной радиации), понятно, следует принимать тем выше, чем более высокая категория дороги. Исходя из указание предпосылок, величину коэффициента φ, дифференцированного по обеспеченности один раз в 100, 50 и 33 года (что соответствует вероятностям 1 %, 2 %, 3 %), рекомендуется принимать по табл. 3.1.

Коэффициент снижения прочности льда.

Таблица 3.1.

Категория дорог		Зоны одинаковых коэффициентов снижения прочности льда φ
железных	автомобильных	1	2	3	4
I-II	I-II	0,55	0,60	0,75	0,95
III-IV	III	0,50	0,55	0,70	0,90
Подъездные и внутренние пути.	IV-V	0,45	0,50	0,65	0,85

3.9. Наряду с предлагаемым методом уточнения прочности льда в зависимости от климатических особенностей региона (по коэффициенту φ) дня водохранилищ и участков рек южнее линии Архангельск Киров - Уфа - Кустанай СНиП 2.06.04-82* допускает принимать прочность льда на сжатие при первой подвижке льда и, в период ледохода соответственно R_c = 0,45 МПа и R_c = 0,3 МПа, а при определении прочности льда на снятие по формуле (3.3), но не выше R_в = 0,45 МПа в период ледохода и R_в = 0,75 МПа - при первой подвижке льда.

Для указанного района (на рис. 3.3 он расположен левее пунктирной линии) к расчету рекомендуется принимать меньшее значение прочностных характеристик льда R_c и R_вполученных по формуле (3.1) с учетом температуры-воздуха (льда) или приведенных в настоящем пункте.

4. НАГРУЗКИ ОТ ЛЕДЯНЫХ ПОЛЕЙ НА ОПОРЫ МОСТОВ.

4.1. В основу расчета ледовых нагрузок на опоры ростов положен принцип, что сила от воздействия льда на сооружения не может быть больше той, при которой происходит разрушение льда. В зависимости от конструктивных особенностей опор различают следующий характер разрушения льда при взаимодействии ледяных полей с опорой моста: прорезание опоры (обычно с заостренной передней гранью); смятие перед опорой при отсутствии заостренной передней грани) со срезом вдоль наружных баковых поверхностей; раздробление льда при остановке или ударе отдельных льдин.

Расчет ледовых нагрузок проводят, как правило, для всех схем разрушения льда, поскольку характер взаимодействия льда с опорой определяется местом приложения нагрузки (в плане и по высоте опоры).

По высоте точку приложения равнодействующей ледовой нагрузки необходимо принимать ниже уровня воды, при котором определяется нагрузка, на 0,3 h_лр%.

4.2. Силу от воздействия ледяных полей при первой подвижке, на отдельно стоящую сваю (сваю-оболочку) или опору с вертикальной передней гранью шириной следует определять по формуле

F_c_м = т·R_в·в h_лр%, (4.1)

где т - коэффициент формы опоры в плане принимаемый равным: для прямоугольной т = 1, цилиндрического или полуциркульного очертания т = 0,9; при передней грани в виде треугольника с углом заострения в плане Q - по формуле (в диапазоне 45° ≤ Q ≤ 120°)

т =0,155 Q^1/3.

Разрушение ледяного покрова перед опорой в рассматриваемом случае происходит за счет смятия или прорезания льда.

На нешироких реках и при небольшой толщине льда сила воздействия ледяного поля на опору мотет оказаться недостаточной для разрушения льда. В этом случае остановившееся ледяное поле воздействует с силой (в МН).

(4.2)

где скорость течения воды подо льдом V (в м/с) расчетную толщину льда h_лр% (в м), площадь ледяных полей А (в м²) и сопротивление, льда смятию R_в (в МПа) определяют соответственно по п.п. 2.11., 2.14 и 3.6; при угле Q > 120°, а также для прямоугольного, цилиндрического и полуциркульного очертания опор в плане следует принимать

К расчету принимают меньшее значение полученное по формулам (4.1) и (4.2).

4.3. Силу от воздействия ледяных полей в период ледохода на опору с вертикальной передней гранью следует определять по формуле

(4.3)

где r плотность воды (ρ = 1000 кг/м³).

Определение скорости движения V льдин, ширины L_л и расчетной толщины льда h_л_p_% изложены в п. 2.

Полученное по формуле (4.3) значение силы F_см необходимо сопоставить с F_p, определенной по формуле (4.1) для того же уровня ледохода, и к расчету принять меньшее значение.

4.4. При наличии наклонной передней грани опоры возможны две принципиально различных схемы взаимодействия ледяных полей с сооружениями, в результате которых происходит:

а) смятие льда перед опорой (или его прорезание), как у опор с вертикальной передней гранью;

б) наползание льдины на наклонную грань с дальнейшим изломом льда под действием собственного веса. Это условие выполняется, если угол наклона поверхности передней грани опору к горизонту β меньше критического β_кр, определяемого по формулам:

при первой подвижке

(4.4)

при ледоходе

(4.5)

где β₀ - угол трения льда по опоре (β₀ = 8÷8,5°);

(для определения K_β можно пользоваться также данными табл. 30 СНиП 2.05.04-82*).

4.5. Вертикальную составляющую силы F_из(в) на опору с наклонной передней гранью при β < β_кр сдует определять по формулам:

при первой подвижке

F_из(в) = K_βR_fh²_лр%; (4.6)

при ледоходе - по формуле (4.3).

Горизонтальная составляющая силы в этом случае равна

F_из(г) = F_из(в) tg(β + β₀) (4.7)

Полученные значения составляющих сил необходимо сопоставить (для соответствующих ледовых режимов):

вертикальную при ледоходе с F_из(в) по формуле (4.6), а горизонтальную с F_см по формуле (4.1). К расчету принимают меньшие значения.

В случае, когда β ≥ β_кр расчет воздействия льда следует проводить как для опор с вертикальной передней гранью, т.е. вертикальную составляющую силы принимать равной нулю, а горизонтальную - по формулам (4.1) - (4.3) с учетом п.п. 4.2 и 4.3.

4.6. При определении силы от воздействия ледяных полей на отдельно стоящую опору с вертикальной или наклонной передней гранью косое направление воздействия ледяных полей следует учитывать при угле между продольной осью опоры и вектором силы γ ≥ 10°.

При косом направлении воздействия ледяных полей наклон передней грани опор не учитывается, и расчет следует производить соответственно по формулам (4.1) и (4.3), в которых принимают: за ширину опоры в - проекцию опоры (в плане) на плоскость, перпендикулярную направлению воздействия ледяных полей; для всех опор, кроме цилиндрических, коэффициент формы опоры в плане т = 1 (для цилиндрической т = 0,9).

4.7. Силу от воздействия ледяных полей на каждый из двух и более элементов поперек направления движения (ледяных полей) с просветами S ≤ 2 h_лр% (см. рис. 3.2) определяют по формуле

(4.8)

где F₁ - сила от воздействия ледяных полей на один элемент шириной в₁ рассматриваемого сооружения, определяемая по вышеприведенным формулам п. 4 для соответствующих ледовых условий, включая косое направление, воздействия ледяных полей, и конструкции опор;

K_вп - коэффициент определяемый по формуле (3.5) для п элементов, входящих в сооружение. На каждый элемент действует сила в п раз меньше, чем на все сооружение.

Если в ряду из п элементов имеется j просветов S > 2 h_лр%, то ряд следует разбить на (j+1) сооружение между которыми просветы S > 2 h_лр%. Расчет каждого из (j+1) сооружения производят по формуле (4.8).

За расчетное воздействие следует принимать наименьшую силу, определенную по формуле (4.8) и формулам, указанным в п.п. 4.3, 4.5 для соответствующих ледовых воздействий.

4.8. При первой подвижке льда на второй и последующие элементы ряда (свай, свай-оболочек и т.п.), расположенные вдоль направления движения ледяных полей на расстоянии друг от друга (по осям) l ≤ l_m_ах (см. рис. 3.2) действует сила F_cp которую рекомендуется определять как доли от силы F_см, действующей на первый элемент ряда,

F_ср = ξ·F_см, (4.9)

где ξ - коэффициент снижения воздействия льда на последующие элементы ряда

(4.10)

где п_ср - число плоскостей среза между элементами ряда (см. п. 4.12);

l_ср - длина плоскости среза (см. п. 4.13);

(4.11)

В СНиП 2.05.03-84* приведено некоторое осредненное значение ξ (хотя его величина дана до третьего знака после запятой) в зависимости только от l/в₁:

l/в₁…	1	1,1	1,2	1,3	1,4	1,5	1,6	1,7
ξ…	0,2	0,204	0,212	0,230	0,28	0,398	0,472	0,542
l/в₁…	1,8	1,9	2	2,1	2,2	2,4	2,5 > 2,6
ξ…	0,608	0,671	0,73	0,785	0,836	0,928	0,967 1

Приведенные в СНиП 2.05.03-84* значения коэффициента ξ не могут выть использованы для расчета двух и более рядов.

4.9. Если элементы ряда (свай, свай-оболочек и т.п. расположенные вдоль направления движения ледяных полей, соединены между собой стенкой толщиной Δ, то при первой подвижке льда на второй и последующие элементы ряда действует сила:

а) при Δ ≤ в₁ sin α

(4.12)

б) при Δ > в₁ sin α

(4.13)

где α - половина угла сектора (см. рис. 3.2), на ширине которого происходит срез льда между столбами (см. п. 4.13).

Максимальное расстояние между элементами ряда (по их осям) l_m_ах, при котором происходит срез льда между этими элементами, определяется по формуле

(4.14)

При l > l_m_ах каждый элемент в ряду, расположенный вдоль направления движения ледяных полей работает независимо друг от друга (у каждого элемента происходит смятие льда).

4.10. При косом направлении нагрузки на второй и последующие элементы ряда, расположенные вдоль движения ледяных полей, совместной работе элементов будет при соблюдении условий l ≤ l_m_ах, где l_m_ах определяется по формуле (4.14), и

l < в₁/sinγ (4.15)

При соблюдении указанных условий на рассматриваемые элементы ряда будет действовать сила характеризующая как смятие, так и сдвиг льда и определяемая по формуле

(4.16)

где F_см - усилие при разрушении ледяного покрова за счет смятия льда, определяемое по формуле (4.1);

F_cp - усилие, при котором происходит срез льда между элементами ряда, определяемое по формуле (4.9) при п_ср =1. Составляющая силы F_γ характеризующая сдвиг, будет только в том случае, если внешняя плоскость сдвига будет "упираться" в нижестоящий элемент (рис. 4.1). Это условие соблюдается при неравенстве (4.15).

При соблюдении указанных выше двух условий для расстояния l между элементами на второй и последующие элементы взаимодействующего рода, расположенного ниже по направлению движения ледяных полей (на рис. 4.1 ряд № 2),будет действовать сила, определяемая по формуле. (4.9) при п_ср = 1.

Если взаимодействующих рядов больше двух, то для последующих элементов внутренних рядов п_ср = 0 (т.е. нагрузки не будет).

При несоблюдении неравенства (4.15) с некоторым запасом принимается, что последующие элементы взаимодействующих (а также невзаимодействующих) рядов рассчитываются как первые элементы в рядах, параллельных направлению нагрузки (см. п. 4.7), т.е. как при l > l_max (см. рис. 4.1)

Под взаимодействующими рядами понимаются ряды, между элементами которых в направлении параллельном поперечной оси опоры просветы S ≤ 2h_лр%.

4.11. Для практических расчетов воздействия, льда в период ледохода на второй и последующие элементы опоры в ряду, расположенном параллельно направлению нагрузки (движения ледяных полей), можно не учитывать, поскольку первые элементы ряда работают как аванпостные сооружения, у которых происходит разрушение ледяных полей.

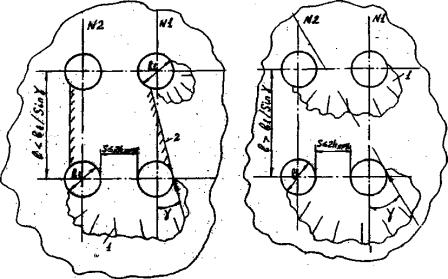
Рис. 4.1. Схема разрушения льда при косом направлении воздействия ледяных полей на элементы опор:

1 - скол (смятие льда); 2 - плоскость среза льда

При косом подходе ледяных полей к опоре (γ ≥ 10°), элементы которой составляют два и более продольных рада, нагрузку воспринимают, кроме первых элементов продольных рядов (как при отсутствии косины), все элементы рада № 1 (см. рис. 4.1).Расчет нагрузки на каждый элемент определяют согласно п. 4.7. Причем, для последующих элементов рада № 1 в расчетах следует принимать S = (l - в₁)sinγ.

4.12. Число плоскостей среза п_ср между элементами ряда расположенного параллельно направлению нагрузки, равно (см. рис. 3.2):

п_ср = 2 при одиночном раде;

п_ср = 1 при двух взаимодействующих рядах;

при трех и более взаимодействующих рядах для крайних п_ср = 1, для внутренних рядов п_ср= 0 (т.е. ледовая нагрузка отсутствует).

За одиночный принимают ряд, который по фронту (поперек направления) нагрузки удален (имеется просвет) от других сооружений (или их элементов) на S > 2h_лр%.

За п ≥ 2 взаимодействующих рядов принимают ряды, которые по фронту направления нагрузки имеют просветы S ≤ 2h_л_p_%.

4.13. Длина плоскости среза l_ср между элементами ряда, параллельного направлению нагрузки, определяется геометрией двух взаимодействующих элементов в ряду

l_ср = l - 1/2в₁cosα, (4.16)

где α - угол сектора элемента опоры в плане (см. рис. 3.2), в пределах которого происходит срез льда. В диапазоне 30° ≤ α ≤ 90° (в градусах)

(4.17)

4.14. Силу от воздействия ледяных полей в период ледохода на опоры мостов через водохранилища следует определять по формуле СНиП 2.06.04-82*

F = A(P_μ+P_v+P_i+P_μa) (4.18)

где А площадь ледяного поля (см. п. 2.15);

P_μ, P_v, P_i, P_μa - составляющие горизонтального давления на опору, определяемые в МПа по формулам:

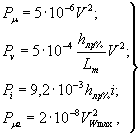(4.19)

где V, V_w_max - расчетные скорости движения ледяных полей и ветра (см. п. 2.13, 2.14);

L_m - средняя длина ледяного поля по направлению ветра (см. п. 2.16);

i - уклон поверхности потока, которым можно, пренебречь, если рассматриваемое направление ветра не совпадает, с направлением потока.

За расчетное воздействие следует принимать наименьшую силу, определенную по (4.18) и формулам, указанным в п.п. 4.3 - 4.5 для соответствующих ледовых воздействий.

4.15. Общая нагрузка на опору, состоящую из п элементов (составляющих продольные и поперечные ряды), определяется как сумма нагрузок на каждый элемент.

Приложение 1

Таблица отклонения ординат кривой вероятностей Пирсона III типа от середины Ф_р% (по Фостеру-Рыбкину)

С_s	Вероятность, %
С_s	1	2	5	10	20	25
3,0	4,02	3,16	2,02	1,18	0,42	0,25
2,75	3,93	3,11	2,02	1,21	0,48	0,27
2,50	3,83	3,04	2,01	1,24	0,53	0,32
2,25	3,72	3,98	2,01	1,27	0,57	0,36
2,00	3,60	2,89	2,00	1,30	0,61	0,39
1,75	3,47	2,80	1,98	1,32	0,65	0,43
1,50	3,33	2,71	1,95	1,33	0,70	0,47
1,25	3,18	2,62	1,92	1,34	0,72	0,52
1,00	3,02	2,53	1,88	1,34	0,76	0,55
0,90	2,96	2,48	1,86	1,34	0,77	0,57
0,80	2,89	2,43	1,84	1,34	0,78	0,58
0,70	2,82	2,37	1,82	1,33	0,78	0,59
0,60	2,75	2,34	1,80	1,33	0,80	0,61
0,50	2,68	2,30	1,77	1,32	0,81	0,62
0,40	2,61	2,25	1,75	1,32	0,82	0,63
0,30	2,54	2,20	1,72	1,31	0,82	0,64
0,20	2,47	2,15	1,70	1,30	0,83	0,65
0,10	2,40	2,10	1,67	1,29	0,84	0,66
0,00	2,33	2,04	1,64	1,28	0,84	0,67
-0,2	2,18	1,92	1,58	1,26	0,84	0,69
-0,4	2,03	1,82	1,52	1,23	0,85	0,71
-0,6	1,88	1,72	1,45	1,20	0,85	0,72
-0,8	1,74	1,60	1,38	1,17	0,85	0,73
-1,0	1,59	1,50	1,32	1,13	0,85	0,73

Приложение 2

БЕЗЗАТОРНЫЙ ПРОПУСК ЛЕДОХОДА ПОД МОСТАМИ.

1. В северных районах России одной из важнейших проблем при пересечении рек является беззаторный пропуск ледохода, которой должен решаться на всех стадиях проектно-изыскательских работ.

2. При трассировании дорог и выборе створов мостов следует избегать участков рек, на которых в естественных условиях образуется заторы льда.

Благоприятные условия для образования авторов льда на участках рек:

с резким поворотом речной долины;

многорукавных или сильно искривленных в плане;

приточных (особенно выше створа перехода).

На прямолинейных участках русел створы перехода нежелательно располагать на участках при сужении русел, особенно если одновременно с сужением происходит его углубление.

3. Если в естественных условиях в районе мостового перехода отсутствуют заторные явления, то для беззаторного пропуска ледохода минимальная длина пролета L_min в назначаемой схеме моста должна удовлетворять условию

(1)

где прочность льда на смятие R_в определяют для условий ледохода, а скорость движения ледяного поля V для уровня воды в бровках русла.

4. Основным мероприятием по уменьшению минимальной длины пролета является устройство наклонных ребер опор. При такой конструкции опор

(2)

Для практических расчетов обычно требуется определить на формулы (2) величину угла β наклона ребра опоры к горизонту, при котором обеспечивается беззаторный пропуск льда под мостом с заданными (имеющимся наличии, возможными изготовить и т.п.) пролетами, L_зaд, не удовлетворяющими условие (1).

Приложение 3

ПРИМЕРЫ ОПРЕДЕЛЕНИЯ РАСЧЕТНОЙ ТОЛЩИНЫ ЛЬДА НА ПЕРИОД ЕГО ПЕРВОЙ ПОДВИЖКИ

ПРИМЕР 1. Определить расчетную толщину льда за зимний период на р. А в районе проектируемого моста, если имеются наблюдения за наибольшей толщиной льда h_maxi за N = 10 лет (см. табл. 1)

Исходные и промежуточные статистические данные для расчета толщины льда.

Таблица 1.

№ п/п	Годы набл.	h_maxi, см.	см
1	2	3	4	5	6
1.	1984	53	-5	25	-125
2.	1985	63	5	25	125
3.	1986	46	-12	144	-1728
4.	1987	60	2	4	8
5.	1988	58	0	0	0
6.	1989	65	7	49	343
7.	1990	54	-4	16	-64
8.	1991	45	-13	169	-2197
9.	1992	78	20	400	8000
10.	1993	58	0	0	0
Итого:		580		832	4362

РЕШЕНИЕ: 1. По формуле (2.3) определим среднюю многолетнюю толщину льда за зимний период с учетом того, что Σh_maxi = 580 (см. гр. 3 в табл. 1)

2. По формуле (2.2) с учетом 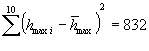(см. гр. 5 табл. 1) среднее квадратическое отклонение от равно

3. Поскольку число лет наблюдений N < 15 лет, для выявления группы наличия данных определим по формуле (2.1) относительную среднюю квадратическую погрешность определения

Следовательно, имеющиеся наблюдения за наибольшей толщиной льда в зимний период, несмотря на N < 15 лет, являются репрезентативными и относятся к первой группе, характеризуемой наличием данных.

4. Для первой группы данных наблюдений принимаем за расчетные полученные значения и σ_л = σ = 9,6 см и по формуле (2.5) определяем коэффициент асимметрии ежегодных максимумов толщин льда (с учетом данных гр. 6 табл. 1)

5. При C_s = 0,73 согласно п. 1.6, а также действующим нормативным документам расчетная вероятность толщины льда должна приниматься равной р_л = 1%.

При C_s = 0,73 и р_л = 1% по Приложению 1 находим ординату кривой вероятности Пирсона III типа от середины Ф_1% = 2,84.

6. По формуле (2.4) расчетная толщина льда за зимний период равна h_max_1% = 58+2,84·9,6 » 83 см.

ПРИМЕР 2. Определить расчетную толщину льда за зимний период h_max_p_% и на период его первой подвижки h_лр% для условий примера 1 при числе лет наблюдений N = 5 (см. табл. 2). Река А находится в районе г. Омска (севернее широты 55°). Средние за 15 лет сумма отрицательных среднесуточных температур воздуха от ледостава до начала снеготаяния и толщина среднего покрова за зимний период равны Σ|t| = 670°С и h_c = 1,0 м.

Исходные и промежуточные статистические данные для расчета толщины льда.

Таблица 2.

№ п/п	Годы набл.	Сумма отр. темп. Σ\|t\|₀, °С	h_maxi, см.	см
1.	1989	690	65	+5	25	125
2.	1990	670	54	-6	36	-216
3.	1991	515	45	-15	225	3375
4.	1992	725	78	18	324	5832
5.	1993	660	58	-2	4	-8
Итого:		3260	300		614	2358

РЕШЕНИЕ: 1. При N = 5 лет наблюдения относятся ко второй группе (недостаточных) данных (см. п. 2.7), для которых средняя толщина льда за 5 лет и среднее квадратическое отклонение от этой средней толщины соответственно по формулам (2.3) и (2.2) с учетом данных табл. 2 равны

Следует обратить внимание, что по полученным результатам формально наблюдения могут быть отнесены к 1-ой группе (достаточных) данных, поскольку по формуле (2.1) Это связано с тем, что для рассматриваемой толщины льда величина действительного коэффициента вариации достаточно мала - близка к 0,1 (Под действительным понимается значение σ при N →¥ в отличии от так называемой смещенной величины коэффициента, определяемой по формуле 2.2).

2. С учетом того, что ряд мал, согласно п. 2.7 примем коэффициент уменьшения σ, равный 0,65, и найдем расчетное значение среднеквадратического отклонения толщин льда для N = 5 лет, т.е. σ_л_N = 12,4·0,65 = 8,1 см. Для полученного значения σ_л_N и данных табл. 2 по формуле (2.5)

3. Для вероятности (толщины льда) и C_s = 1,85 по Приложению 1 находим отклонение ординаты кривой Пирсона III типа от середины Ф_1/_N = 0,64.

Из имеющихся за пять лет наблюдений толщин льда за зимний период выбираем наибольшую толщину (в 1992 году) h_maxN = 78 см и по формуле (2.7) определяем среднюю толщину льда

4. При C_s = 1,85 согласно п. 1.6, а также действующим нормативным документам расчетная вероятность толщины льда должна приниматься равной р_л = 1%. Для этих данных по Приложению 1 Ф_1% =3,52.

По формуле (2.4) расчетная толщина льда за зимний период (1 % вероятности) равна

h_max_1% = 73+3,52·8,1 » 102 см.

Полученное значение более чем на 20% больше толщины льда в Примере 1. Это связано с тем, что за малое число лет наблюдений встретилась толщина льда (в 1992 году), вероятность которой явна выше 20%.

5. Определим расчетную толщину льда с использованием формулы (2.6) согласно п. 2.7.

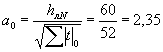Из табл. 2 и искомый параметр (Согласно п. 2.6 ).

Подставляем а₀ = 2,35 и Σ|t|=670 в формулу (2.6)

6. По рис. 2.1 принимаем σ_л = 10 см и C_s = 0,5, а по Приложению 1 при р_л = 1% (см. табл. 1.3) Ф_1% = 2,68. По формуле (2.4) расчетная толщина льда

h_max_р% = 61 + 2,68·0,1 = 88 см.

7. Сопоставляя полученные значения толщин h_max_p_% по способам (102 см и 88 см) к расчету следует принимать наибольшую. Но поскольку из данных наблюдений за 10 лет (см. табл. 1 примера 1) нами выявлено явное завышение толщина льда h_max_р% = 102 см (см. п. 4), то к расчету следует принимать h_max_р% = 88 см.

Для дальнейших расчетов будем принимать толщину h_max_р% = 83 см, подученную в Примере 1 по прямым (а не косвенным) исходным данным.

8. Согласно п. 2.8 коэффициент α = 0,8. По формуле (2.8) расчетная толщина льда, на период его первой подвижки

h_лр_% = 0,8·83 = 67 см.

Приложение 4

ПРИМЕРЫ РАСЧЕТА НАГРУЗОК ОТ ЛЕДЯНЫХ ПОЛЕЙ НА ОПОРЫ МОСТОВ

ПРИМЕР 1. Для условий примеров в приложении 3 (река А в районе г. Омска, расчетная толщина льда к периоду первой подвижки h_лр_% = 67 см), а также расчетной температуре льда t_ap = -1,8°С определить наибольшую ледовую нагрузку на опоры автодорожного моста на дороге III категории. Опоры безростверкового типа из четырех свай-оболочек диаметром в₁ = 1,6 м, расположенных а один ряд вдоль течения (и вдоль направления ледовых воздействий). Расстояние между сваями по осям l = 3,2 м.

РЕШЕНИЕ:

1. Согласно п. 3.4 для температуры льда t_ap = -1,8°С по интерполяции нормативное сопротивление льда сжатию равно R^н_c » 0,63 МПа.

2. Мостовой переход находится во 2-ой зоне районирования коэффициента φ снижения прочности льда под влиянием солнечной радиации (см. рис. 3.3).Для автодорог III категории согласно табл. 3.1 принимаем φ = 0,55. Тогда расчетную прочность льда на сжатие перед его первой подвижкой определим по формуле (3.1)

R_с = 0,55×0,63 = 0,346 МПа.

3. Разрушение ледяного покрова перед проектируемой опорой будет происходить за счет смятия льда. Для определения прочности льда на смятие R_в согласно формулы (3.5) вначале найдем численное значение коэффициента К_в. При в = в₁ по формуле (3.6)

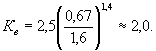
Из формулы (3.5)

R_в = 2,0×0,346 = 0,692 МПа.

4. Силу от воздействия ледяных полей при первой подвижке на переднюю сваю оболочку определим по формуле (4.1) при m = 0,9 (опора цилиндрического сечения)

F_см = 0,9×0,692×1,6×0,67 = 0,67 МН.

5. Для выявления взаимодействия ниже расположенных свай-оболочек с первой и между собой следует сопоставить расстояние между ними l с критериальным, определяемым по формуле (4.4)

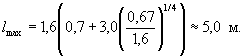
Поскольку l < l_max элементы ряда взаимодействуют друг с другом. На второй и последующие элементы ряда будет действовать сила, определяемая по формуле (4.9) и характеризующая срез льда между сваями-оболочками.

6. В формулах (4.9) и (4.10) принимаем: число плоскостей среда между элементами n_c_р = 2, поскольку ряд одиночный (см. п. 4.12 и на рис. 3.2 правый ряд вдоль потока);

длину плоскостей среза l_ср по формуле (4.16) при угле сектора элемента в плане по формуле (4.17)

прочность льда на срез по формуле (3.7) R_cp = 1/3×0,346 » 0,115 МПа,

7. Подставляя полученные величины в формулу (4.9), найдем силу, действующую на вторую-четвертую сваю оболочку, из которых состоит опора. По формуле (4.10)

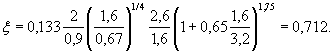
Тогда F_cp = 0,67×0,712 = 0,477 МН.

8. На всю опору (ряд) из четырех свай-оболочек действует сила, равная сумме нагрузок на каждый элемент, т.е.

ΣF = 0,67+3·0,477 = 2,1 МН.

9. Отметим, что в период ледохода вторая-четвертая сваи не воспринимает ледовую нагрузку (см. п. 4.11), а на первую действует сила, определяемая по формуле (4.3).

Для определения величины этой силы примем скорость движения льдин V = 2 м/с, а ширину льдин L_л = 30 м. Тогда

Формально полученный результат следует сопоставить с силой F_см (по формуле 4.1) для условий ледохода (т.е. R_с = 0,55×0,44 = 0,242 МПа и R_в = 2×0,242 = 0,484 МПа), хотя априори ясно, что F_p < F_см. Действительно, F_см = 0,9×0,484x×1,6×0,67 = 0,47 МН.

Таким образом, при ледоходе на всю опору действует сила F_p = 0,06 МН.

ПРИМЕР 2.

Для условий примера 1 проверить возможность беззаторного пропуска ледохода под мостом с использованием пролетов L_зад. = 21 м., если скорость движения ледяного поля на уровне воды в бровках русла V =1,7 м/с. Определить усилие на элементы и всю опору при устройстве ледореза в виде наклонной сваи-оболочки у передней сваи-оболочки.

РЕШЕНИЕ:

1. Проверка производится по неравенству (1) Приложения 2, в котором R_в = 0,484 МПа = 0,484·10⁶ Па (см. п. 9 предыдущего примера) и можно принять L_л/В_р = 0,1.

Формально неравенство (1) решается подбором. При L_min = 21 м правая часть неравенства равна

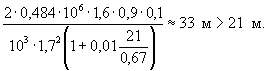
Поэтому, пролеты L_зад. не обеспечивают беззаторный пропуск ледохода под мостом.

Если требуется определить необходимый минимальный пролет, то подбирают такой L_min в знаменателе формулы (1), при котором правая часть этой формулы равнялась бы подобранному L_min. Это условие соблюдается при L_min = 33 м, т.е. имеющегося типоразмера для пролетов автодорожных мостов.

2. Для использования L_зад. = 21 м возможно устройство ледорезов (например, в виде наклонной сваи-оболочки такого же размера у передней сваи). Угол наклона ледорезной части опоры к горизонту может быть определен из формулы (2) Приложения 2. В этой формуле, кроме угла β неизвестна прочность льда на изгиб. Из формулы (3.4) и R_с = 0,242 МПа (на период ледохода), R_f = 0,75·0,242 = 0,181 МПа = 0,181·10⁶ Па.

Для L_зад. = L_min = 21 м из формулы (2)

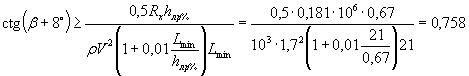
откуда β + 8 » 53° и β = 53 - 8 = 45°.

3. При устройстве ледорезной сваи с наклоном к горизонту β ≤ 45° (примем β = 44°) в период ледохода будет происходить наползание на нее льдин с дальнейшим изломом льда под действием собственного веса, т.е. будет удовлетворяться неравенство (4.5).

Тогда согласно п. 4.5 вертикальная сила на ледорезную сваю в период ледохода по формуле (4.3)

Полученное значение силы следует сравнить с величиной по формуле (4.6)

При

F = 1,12·0,181·10⁶·0,67² = 0,091 МН > 0,027 МН.

Поэтому к расчету принимаем F_из(в) = 0,027 МН.

По формуле (4.7) горизонтальная сила равна F_из(_г) = 0,027·tg (44°+ 8°) = 0,027·1,28 » 0,035 МН, что априори меньше силы по формуле (4.1), при которой происходит смятие льда.

Следовательно, при ледоходе на всю опору будет действовать горизонтальная сила F_из(_г) = 0,035 МН.

4. При первой подвижке возможность наползания льда на опору проверим по неравенству (4.4)

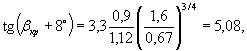
т.е. β_кр » 71° > β = 44°.

Поэтому наползание льда будет иметь место, и горизонтальную составляющую силы на наклонную опору определим по формуле (4.7) с учетом (4.6). При R_f = 0,75 R_c = 0,75·0,346 = 0,27 МН.

F_из(_г) = 1,12·0,27·0,67²·tg 52° = 0,174 МН,

что меньше F_c_м = 0,67 МН (см. пример 1.)

5. Для определения суммарной нагрузки на ряд свай при первой подвижке льда неизвестно только усилив на первую сваю, к которой подставлена наклонная свая. Пусть на уровне льда (при первой подвижке) расстояние в осях между вертикальной и наклонной сваей l =2,0 м. Тогда длина плоскости среза льда между этими сваями по формуле (4.14) l_ср = 2,0 - 0,5·1,6 cos 42,5° = 1,6 м, а сила действующая на вертикальную сваю, по формуле (4.9).

При l_ср = 2 - 1/2·1,6 cos 33,5° = 1,33 м,

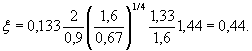
F_cp = 0,44·0,67 = 0,295 МН.

Суммарная нагрузка на всю опору (при усилиях на вторую-четвертую сваю равных F_cp = 0,477 МН (см. пример 1)

ΣF = 0,174+0,295+3·0,477 = 1,9 МН.

Нагрузка оказалась практически такой же, как при отсутствии наклонной сваи (из примера 1 ΣF = 2,1 МН), но существенно уменьшилось усилие на первую вертикальную сваю.

ПРИМЕР 3.

Для условий примера 1 подобрать толщину стенки, соединяющей сваи, чтобы суммарное усилие на опору при первой подвижке сократилось до 1 МН.

РЕШЕНИЕ:

1. Задача решается подбором. Вначале определим величину в sin α = l,6·sin 42,5° = 1,08 м.

2. При Δ = 1,0 м при F_см = 0,67 МН, ξ = 0,712 (см. пример 1) и 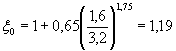по формуле (4.12) усилие на вторую-четвертую опору равно

Суммарное усилие ΣF = 0,67+3·0,105 = 0,985 МН, т.е. с первого раза подобрана требуемая толщина стенки.

3. Для иллюстрации влияния толщины стенки между сваями на величину усилий на них примем Δ = 0,5 м, т.е. меньше в sin α, и Δ = 1,2 м > в sin α.

При Δ = 0,5 м.

т.е. усилие на сваю возросло почти в три раза.

При Δ = 1,2 м 1 - Δ/в = 1 - 1,2/1,6 = 0,25 и 1 - sin 42,5° = 0,325 по формуле (4.13)

ПРИМЕР 4.

Исходные данные, как в Примере 1, но опора двухрядная. Между рядами просвет S = 0,8 м. Определить наибольшую (при первой подвижке льда) ледовую нагрузку на опору.

РЕШЕНИЕ:

1. Поскольку, S < 2h_лр% то продольные ряды свай-оболочек будут взаимодействовать друг с другом - около первых элементов рядов будет происходить "общее" смятие льда (см. рис. 3.2).

2. На первые элементы рядов будет действовать сила, определяемая по формуле (4.8).

В указанной формуле: F₁ - сила от воздействия ледяного поля (при первой подвижке) на первой элемент ряда при однорядовой опоре, т.е. f_см = 0,67 МН; К_в_n - коэффициент, определяемый по формуле (3.6) при

в = 2 в₁+S = 2·1,6+0,8 = 4,0 м

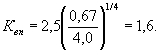
С учетом того, что К_в = 2 (согласно проведенным расчетам в Примере 1), ледовая нагрузка на каждую из двух первых свай оболочек равна

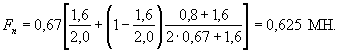
Полученный результат не надо сопоставлять с какими-либо другими расчетами, поскольку за основу при определении нагрузки взята формула (4.1), характеризующая смятие льда у сооружения (см. п. 4.2).

3. На вторые и последующие сваи-оболочки в рядах действуют силы, возникающие при срезе льда между сваями и определяемые по формуле (4.9), как в Примере 1. Отличие состоит только в том, что число плоскостей среза при двух рядах свай п_c_р = 1 (см. п. 4.12 и рис. 3.2). Тогда (см. пример 1) ξ = 0,356 и F_cp = 0,625·0,356 = 0,222 МН.

Эта сила является расчетной (см. п. 7 примера 1).

4. Суммарная ледовая нагрузка на всю опору равна

Σf = 0,625·2+2·3·0,222 = 2,78 МН.

Следует обратить внимание, что при увеличении числа свай-оболочек в два раза (по сравнению с однорядной опорой в Примере 1) ледовая нагрузка увеличилась только в 2,78/2,1=1,32 раза.

ПРИМЕР 5.

Определить наибольшую (при первой подвижке льда) ледовую нагрузку на опору в Примере 4, если направление нагрузки составляет с продольной осью рядов угол γ = 20°(см. рис. 4.1).

РЕШЕНИЕ:

1. На первые сваи-оболочки в рядах будут действовать такие же силы, как и при отсутствии косого направления воздействия ледяных полей (см. п. 4.7), т.е. по f = 0,625 МН.

2. Из примера 1 известно, что в рядах из свай-оболочек соблюдается условие l < l_max. Определим второе необходимое условие (4.15), при котором осуществляется совместная работа свай-оболочек в рядах

в₁/sin γ = 1,6/sin20° = 4,68 м > l = 3,2 м

Условие (4.15) соблюдается. Поэтому на второй-четвертый элементы в ряду, расположенном вдоль движения ледяных полей, будет действовать сила, характеризующая как смятие, так и сдвиг льда (см ряд. № 1 на левом фрагменте рис. 4.1).

Силу от воздействия льда на эти элементы ряда определяют по формуле (4.16), в которой F_см = 0,67 МН (см. п. 4 примера 1), a F_cp = 0,222 МН (см. п. 3 Примера 4).

3. На второй-четвертый элементы нижнего ряда (№ 2 на левом фрагменте рис. 4.1) будет действовать сила F_cp = 0,222 МН.

4. Суммарная ледовая нагрузка на всю опору равна

Σf = 2·0,625 + 3·0,53 + 3·0,222 = 3,51 МН.

При отсутствии косины ледовая нагрузка для такой же опоры составляет 2,78 МН (см. Пример 4).

СПИСОК ОСНОВНОЙ ЛИТЕРАТУРЫ

1. Пособие к СНиП 2.05.03-84 "Мосты и трубы" По изысканиям и проектированию железнодорожных и автодорожных мостовых переходов через водотоки". (ПМП-91). М., ПКТИтрансстрой, 1992, 411 с.

2. Наставление гидрометрическим станциям и постам. Вып. 6. Часть I Л., Гидрометеоиздат, 1978, 384 с.

3. СНиП 2.06.04-82*. Нагрузки и воздействия на гидротехнические сооружения (волновые, ледовые и от судов)/Госстрой СССР - М: ЦИТП Госстрой СССР, 1989, 40 с.

4. СНиП 2.01.14-83. Определение расчетных гидрологических характеристик /Госстрой СССР. М., Стройиздат, 1985, 36 с.

5. СНиП 2.05.03-84. Мосты и трубы /Госстрой СССР. - М: ЦИТП Госстроя СССР, 1988, 200, с