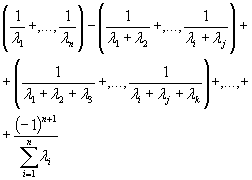|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ |
||
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р 51901.15- 2005 (МЭК 61165:1995) |
Менеджмент риска
ПРИМЕНЕНИЕ МАРКОВСКИХ МЕТОДОВ
IEC 61165:1995
Application of Markov techniques (MOD)
|
|
Москва Стандартинформ 2005 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1. ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО НИЦ КД) на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2. ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии России от 30 сентября 2005 г. № 236-ст
4. Настоящий стандарт является модифицированным по отношению к международному стандарту МЭК 61165:1995 «Применение марковских методов» (IEC 61165:1995 «Application of Markov techniques») путем внесения технических отклонений, объяснение которых приведено во введении к настоящему стандарту.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
Изменения, введенные в настоящий стандарт по отношению к международному стандарту, обусловлены необходимостью наиболее полного достижения целей национальной стандартизации
5. ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет.
Содержание
Введение
Настоящий стандарт входит в комплекс стандартов по менеджменту риска и в части методов анализа риска развивает и дополняет ГОСТ Р 51901-2002 «Управление надежностью. Анализ риска технологических систем».
Марковский анализ является одним из аналитических методов анализа надежности и может использоваться для оценки и анализа вероятностных характеристик технических систем на этапе оценки и анализа риска.
Относительные достоинства различных методов и возможность их индивидуального или комплексного применения для оценки вероятностных характеристик данной системы или компонента должны исследоваться до принятия решения об использовании методов марковского анализа. Для каждого метода необходимо изучить получаемые результаты, необходимые данные, сложность анализа и другие определяющие факторы.
В отличие от применяемого международного стандарта в настоящий стандарт не включена ссылка на МЭК 60050 (191): 1990 «Международный электротехнический словарь. Глава 191. Надежность и качество обслуживания», которые нецелесообразно применять в национальном стандарте из-за отсутствия принятого гармонизированного национального стандарта. В соответствии с этим изменено содержание раздела 3.
|
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ |
|
Менеджмент риска ПРИМЕНЕНИЕ МАРКОВСКИХ МЕТОДОВRisk management. Application of Markov techniques
|
Дата введения - 2006-02-01
1 Область применения
Настоящий стандарт устанавливает руководство по применению марковских методов анализа надежности
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ Р 51901.14-2005 (МЭК 61078:1991) Менеджмент риска. Метод структурной схемы надежности
ГОСТ Р 51901.5-2005 (МЭК 60300-3-1:2003) Менеджмент риска. Руководство по применению методов анализа надежности.
Примечание: При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный документ заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться замененным (измененным) документом. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте использованы следующие термины и определения:
3.1 элемент (unit): Компонент или набор компонентов, которые функционируют как самостоятельный объект.
Примечание: Элемент может существовать только в двух состояниях: работоспособном или неработоспособном (см. 3.3 и 3.4). Для удобства обозначения состояния элемента в настоящем стандарте используется термин «состояние элемента».
3.2 состояние системы (system state): Специфическая комбинация состояний элементов.
Примечание: Несколько состояний системы могут быть объединены в одно состояние.
3.3 работоспособное состояние (functional state): Состояние системы (элемента), в котором система (элемент) исполняет требуемую функцию.
3.4 неработоспособное состояние (failed state): Состояние системы (элемента), в котором система (элемент) не исполняет требуемую функцию.
Примечание: Система может иметь несколько различных неработоспособных состояний.
3.5 переход (transition): Изменение одного состояния системы (элемента) на другое, обычно происходящее в результате ее (его) отказа или восстановления.
Примечание: Переход может быть также вызван другими событиями, такими как человеческие ошибки, внешние события, реконфигурации программного обеспечения и т.д.
3.6 вероятность перехода (transition probability): Вероятность перехода системы (элемента) из одного состояния в другое.
3.7 начальное состояние (initial state): Состояние системы в начальный момент времени t = 0.
Примечание: После отказа система может быть восстановлена до начального состояния. Обычно система начинает функционировать в момент времени t = 0 из работоспособного состояния, в котором все элементы системы функционируют, и переходит в неработоспособное состояние через другие функциональные состояния, имеющие меньшее количество функционирующих элементов.
3.8 состояние поглощения (absorbing state): Состояние, из которого переходы невозможны.
Примечание: В состоянии поглощения система будет оставаться до тех пор, пока не будет полностью заменена функционирующей системой.
3.9 восстанавливаемая система (restorable system): Система, содержащая элементы, которые могут быть восстановлены после отказа до работоспособного состояния без обязательного появления отказа всей системы.
Примечания
1. Восстановление связано с переходами в диаграмме состояний и переходов в направлении к начальному состоянию. При этом, чтобы система функционировала, соответствующие элементы должны быть зарезервированы.
2. Для восстанавливаемой системы можно вычислить такие показатели надежности как вероятность безотказной работы, среднюю наработку до первого отказа и коэффициент готовности.
3.10 невосстанавливаемая система (non-restorable system): Система, диаграмма состояний и переходов которой содержит только переходы в направлении к состоянию отказа системы.
Примечание: Для невосстанавливаемой системы могут быть определены такие показатели надежности как вероятность безотказной работы и средняя наработка до первого отказа.
4 Обозначения и сокращения
4.1 Обозначения для диаграммы состояний и переходов
4.1.1 символ состояния (state symbol): Состояние изображается в виде круга или прямоугольника.
4.1.2 описание состояния (state description): Описание состояния, помещенное внутри символа состояния и изображенное в виде слов или алфавитно-цифровых символов, определяющих те комбинации отказавших и функционирующих элементов, которые характеризуют это состояние.
4.1.3 знак состояния (state label): Число в круге, расположенное рядом с символом состояния или, при отсутствии этого символа, без него.
Примечание: Состояние часто изображается в виде круга с числом, обозначающим состояние.
4.1.4 стрелка перехода (transition arrow): Стрелка перехода, указывающая направление перехода (в результате отказа или восстановления).
4.1.5 интенсивности (rates): Интенсивности восстановления и/или интенсивности отказов, указанные на стрелке перехода.
4.2 Другие символы и сокращения
В настоящем стандарте используются следующие символы и сокращения: R(f) - вероятность безотказной работы.
Примечание: Для вероятности безотказной работы также используется более общий символ R(tbt2);
MTTF - средняя наработка до отказа;
MTTFF - средняя наработка до первого отказа;
MTBF - средняя наработка на отказ;
MTTR - среднее время восстановления;
λ(t) - интенсивность отказов;
μ(t) - интенсивность восстановлений.
Примечание: Символ M(t) используется также для обозначения интенсивности ремонта;
A(t) - коэффициент готовности в момент времени t;
А(∞) -асимптотический коэффициент готовности.
Примечание: Символ А используется для обозначения асимптотического коэффициента готовности;
MUT - средняя продолжительность работоспособного состояния;
MDT - среднее время простоя;
Pi(t) - вероятность обнаружения системы в состоянии в момент времени t;
Δt - малый интервал времени.
4.3 Пример
На рисунке 1 изображен пример диаграммы состояний и переходов для системы с одним элементом.
![]()
0 - работоспособное состояние системы; 1 - неработоспособное состояние (отказ) системы; λ(f)Δ(t) - вероятность перехода между состояниями 0 и 1 в интервале времени Δt.
Рисунок 1 - Диаграмма состояний и переходов невосстанавливаемой системы с одним элементом
Обычно выражение λ(t)Δt заменяется на λ, поскольку в настоящем стандарте λ(t) является постоянной во времени величиной (раздел 6). На стрелках перехода чаще указывают интенсивности перехода, чем вероятности перехода. Следовательно, диаграмму, представленную на рисунке 1, можно изобразить в упрощенном виде (рисунок 2).
![]()
Рисунок 2 - Диаграмма состояний и переходов для невосстанавливаемой системы с одним элементом
5 Общие положения
При применении методов марковского анализа используют диаграмму состояний и переходов, которая является графическим представлением функционирования системы и моделирует аспекты надежности поведения системы во времени. В настоящем стандарте система рассматривается как набор элементов, каждый из которых может существовать только в одном из двух состояний: неработоспособном или работоспособном. Система в целом, однако, может существовать в различных состояниях, каждое из которых определяется специфической комбинацией работоспособного и неработоспособного состояний ее элементов. Таким образом, в момент отказа или восстановления элемента система переходит из одного состояния в следующее. Обычно эту модель называют моделью дискретных состояний с непрерывным временем. В соответствии с этим способом представления изменения состояний системы применяют методологию анализа пространства состояний.
Анализ пространства состояний применяют при исследовании надежности систем с резервированием или систем, отказ которых зависит от последовательных событий, или систем со сложными стратегиями технического обслуживания (приоритетное восстановление, проблемы организации очереди, ограниченный ресурс). Используемая для анализа надежности системы модель дискретных состояний должна отражать функционирование системы в отношении стратегий и политики технического обслуживания.
Главным преимуществом применения методов марковского анализа с учетом ограничений, описанных в разделе 6, является то, что стратегии технического обслуживания, например, приоритеты восстановления, можно легко смоделировать. Кроме того, в модели можно отразить порядок, в котором происходят многократные отказы. Необходимо отметить, что другие методы анализа надежности, например анализ дерева неисправностей и метод структурной схемы надежности, не позволяют учесть сложные стратегии технического обслуживания.
Хотя анализ пространства состояний с теоретической точки зрения является гибким и универсальным, при решении трудных практических задач необходимы специальные меры предосторожности.
Главная проблема заключается в том, что количество состояний системы и возможных переходов быстро возрастает с ростом количества элементов в системе. В случае большого количества состояний и переходов велика вероятность ошибок и искажений. Чтобы уменьшить это явление, желательно использовать некоторые правила составления диаграммы. Кроме того, используемые расчетные методы могут быть достаточно сложны и могут требовать применения специальных компьютерных программ и/или помощи экспертов в области прикладной математики.
Кроме того, что методы марковского анализа подходят для моделирования стратегий технического обслуживания, они также дают возможность графически отображать процесс отказов/восстановлений, который представляют в виде переходов от одного символа состояния к другому, вместе составляющих диаграмму состояний и переходов системы. Сумма всех вероятностей состояний равна единице. В любой момент времени системе соответствует только одно состояние в диаграмме состояний и переходов. Если по практическим причинам состояния с низкой вероятностью опущены, выполнение вышеупомянутого условия будет только приближенным.
Описанные методы моделирования могут также применяться к системам, в которых некоторые или все элементы являются невосстанавливаемыми. Очевидно, что система с невосстанавливаемыми элементами может рассматриваться как специальный случай системы с восстанавливаемыми элементами, у которых время восстановления будет бесконечным.
6 Предположения
Правила разработки диаграммы состояний и переходов, установленные в настоящем стандарте, применимы во всех случаях. Однако описание расчетных методов приводится только для случая, когда интенсивности отказов и восстановлений для всех элементов исследуемой системы постоянны во времени. Предположение о постоянстве интенсивности отказов приемлемо для компонентов многих систем, но предположение о постоянной интенсивности восстановлений должно быть проверено, если среднее время восстановления элементов не является незначительным по сравнению с соответствующим средним временем наработки на отказ. Числовые оценки в общем случае, когда интенсивности отказов или интенсивности восстановлений не постоянны во времени, в настоящем стандарте не рассматриваются.
Из сделанных предположений следует, что будущее состояние системы зависит только от существующего состояния системы, а не от того, как система оказалась в этом состоянии. Необходимо гарантировать, что диаграмма состояний и переходов обладает указанным свойством, даже если для реальной системы это не так (7.3.2).
Предположения, связанные с вероятностью перехода, можно сформулировать следующим образом:
- переходы состояний являются статистически независимыми событиями;
- интенсивность отказов λ и интенсивность восстановлений μ постоянны;
- вероятности перехода из одного состояния в другое в интервале времени Δt (Δt - мало) задаются величинами λΔt и/или μΔt.
7 Построение диаграммы состояний и переходов
7.1 Предостережения
Основная задача марковского анализа - разработка диаграммы состояний и переходов. Основные правила разработки диаграммы приведены в 7.2. Они должны быть установлены до начала проведения анализа. Это обеспечивает необходимую идентификацию отдельных состояний и, таким образом, позволяет создать четкие графические модели.
7.2 Правила
Рекомендуется использовать следующие правила построения диаграмм:
a) Каждое состояние системы должно быть изображено в виде символа (круг или прямоугольник) с идентификатором состояния (символ или число), который позволяет аналитической процедуре однозначно распознавать это состояние.
b) При необходимости символ может включать описание состояния системы или словесное, или в виде символов в соответствии с принятыми обозначениями. Если используется словесное описание, идентификатор состояния должен располагаться в круге или маленьком прямоугольнике рядом с символом состояния.
c) Состояния должны размещаться так, чтобы крайнее левое состояние было полным работоспособным состоянием системы, а крайнее правое - состоянием отказа системы. Соответственно промежуточные состояния должны быть расположены так, чтобы переход слева направо являлся результатом отказа, а переход справа налево - результатом ремонта или восстановления. Необходимо стремиться к тому, чтобы количество пересечений линий перехода было минимальным.
d) Состояния системы, соответствующие одинаковому количеству отказавших элементов, должны располагаться друг под другом.
e) Переходы между состояниями системы должны быть отмечены линиями со стрелками, соединяющими состояния. Линия со стрелкой справа представляет отказ, а линия со стрелкой слева - восстановление. Если переход между двумя состояниями может быть достигнут путем отказа или восстановления, то такой переход должен изображаться одной линией со стрелками на обоих концах. В простой диаграмме состояний и переходов отдельные линии перехода могут использоваться для индикации отказа или восстановления.
f) На линиях переходов должны быть указаны соответствующие интенсивности переходов. Их можно указать непосредственно на линиях или в отдельном списке.
g) Линии перехода, связанные с невосстанавливаемыми элементами, могут иметь только одну стрелку, которая представляет переход к отказу. Системы, у которых все элементы являются восстанавливаемыми и не имеют ограничений для технического обслуживания с немедленным восстановлением после отказа, должны изображаться на диаграмме со стрелками от и к каждому элементу. Частично восстанавливаемые системы, содержащие как восстанавливаемые, так и не восстанавливаемые элементы, или системы с приоритетами восстановления, должны изображаться с помощью линий перехода, некоторые из которых имеют две стрелки, а другие - только одну. Чтобы улучшить читаемость диаграммы, две стрелки между состояниями должны объединяться в одну там, где это возможно.
h) По возможности, каждый переход должен связывать только соседние состояния. Если отказ вызывает переход системы в другое (не соседнее) состояние, переход изображают в виде дуги.
7.3 Примеры
7.3.1 Система с одним элементом
Применение метода марковского анализа начинают с определения состояния системы. В качестве примера рассмотрим систему с одним элементом. В самом простом случае соответствующая диаграмма состояний и переходов включает только два состояния: работоспособное состояние с интенсивностью отказов λ и неработоспособное состояние с интенсивностью восстановлений μ (рисунок 3).
![]()
0-работоспособное состояние системы; 1-неработоспособное состояние системы.
Рисунок 3 - Диаграмма состояний и переходов для восстанавливаемой системы с одним элементом
Стрелка от состояния 0 к состоянию 1 обозначает появление отказа с вероятностью λΔ(t) в течение времени Δt, стрелка от состояния 1 к состоянию 0 - завершение восстановления системы с вероятностью μΔt в течение времени Δt.
Систему с одним элементом можно изобразить, используя больше чем два состояния (работоспособное и неработоспособное). Ухудшенное состояние, в котором система все еще является работоспособной, также может быть включено в диаграмму (рисунок 4).
![]()
0 - состояние полного функционирования системы; 1 - ухудшенное состояние системы; 2 - неработоспособное состояние системы (состояние поглощения) системы.
Рисунок 4 - Диаграмма состояний и переходов для системы с одним элементом с использованием трех состояний
Если восстановление может быть выполнено из состояния 2, система может быть описана диаграммой, изображенной на рисунке 5, на котором интенсивность восстановлений μ2 представляет переход из состояния 2 в состояние 1.
![]()
0 - состояние полного функционирования системы; 1 - ухудшенное состояние системы; 2 - неработоспособное состояние системы (состояние поглощения).
Рисунок 5 - Диаграмма состояний и переходов для системы, изображенной на рисунке 4, когда восстановление системы может быть выполнено из состояния 2.
Во многих случаях должен рассматриваться прямой путь системы к отказу из состояния 0 к состоянию 2. В этих случаях добавляют стрелку λ3 (рисунок 6).

0 - работоспособное состояние системы; 1 - состояние поглощения; 2 - неработоспособное состояние системы (состояние поглощения).
Рисунок 6 - Диаграмма состояний и переходов для системы, изображенной на рисунке 4, когда возможен прямой путь отказа из состояния 0 в состояние 2
Диаграмма, изображенная на рисунке 3, может использоваться для определения коэффициента готовности A(t) в момент времени t и асимптотического коэффициента готовности А(∞). Для оценки вероятности безотказности работы R(t) применима диаграмма состояний и переходов, изображенная на рисунке 7, в которой состояние 1 является состоянием поглощения.
![]()
0 - работоспособное состояние системы; 1 - состояние поглощения
Рисунок 7 - Диаграмма состояний и переходов для оценки вероятности безотказной работы системы с одним элементом
7.3.2 Система с двумя элементами
Поскольку элемент может быть представлен двумя состояниями: 0 (работоспособное) и 1 (неработоспособное), возможны четыре состояния системы с двумя элементами (0 0), (0 1), (1 0), (1 1). Если система с двумя элементами является последовательной системой, то символ (0 0) обозначает ее единственное работоспособное состояние, а (0 1), (1 0), (1 1) - неработоспособные состояния. Если в системе с двумя элементами используется нагруженный или ненагруженный резерв, то состояния (0 0), (0 1), (1 0) являются работоспособными состояниями. Далее будет рассматриваться система с двумя элементами в нагруженном резерве.
Диаграмма состояний и переходов системы (последовательной или параллельной) с двумя невосстанавливаемыми элементами изображена на рисунке 8.
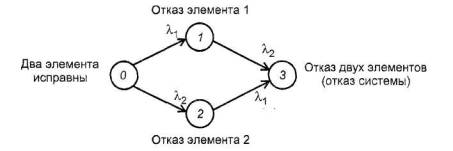
Рисунок 8 - Диаграмма состояний и переходов для системы с двумя невосстанавливаемыми элементами
Примечание: Символы состояний могут иметь вид: (0 0), (0 1), (1 0), (1 1)
Диаграмма состояний и переходов системы с двумя восстанавливаемыми элементами изображена на рисунке 9. Дополнительные стрелки указывают на восстановление с интенсивностями μi(i = 1,2).
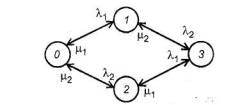
Рисунок 9 - Диаграмма состояний и переходов для системы с двумя восстанавливаемыми элементами
Общая причина отказа может быть изображена в виде прямой перехода от состояния 0 к состоянию 3 с интенсивностью λ3. (рисунок 10).
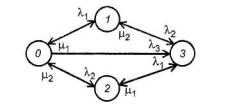
Рисунок 10 - Диаграмма состояний и переходов для системы с общей причиной отказа.
Если отказ с общей причиной отключает одновременно два элемента в восстанавливаемой системе отказ с, возможно, что время, необходимое для восстановления системы после этого отказа (возвращение из состояния 3 в состояние 0), значимо отличается от времени, необходимого для восстановления системы после отказа отдельных элементов. Таким образом, после того как система достигла неработоспособного состояния, будущие действия (тип восстановления) зависят от того, как система оказалась в этом состоянии, что нарушает предположения модели. Для восстановления этого свойства модели необходимо, чтобы действия по восстановлению системы были отражены в диаграмме в соответствии с рисунком 11.
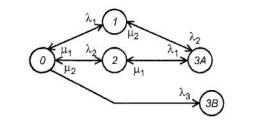
3А, 3В - неработоспособные состояния системы
Рисунок 11 - Диаграмма состояний и переходов для системы с общей причиной отказа
В качестве примера рассмотрим систему с двумя резервными генераторами, которые не включаются при низкой температуре. Когда система достигает состояния «оба генератора не включились», время восстановления будет зависеть от того, находится ли каждый генератор в неработоспособном состоянии из-за механического отказа или оба генератора вышли из строя вследствие общей причины, например из-за воздействия низкой температуры. Поэтому необходимо рассмотреть состояние «оба генератора не включились по причине независимых неисправностей» отдельно от состояния «оба генератора не включились вследствие общей причины». Однако для пользователя системы может быть важно только то, что «оба генератора отказали», а не причины этих отказов. Поэтому необходимо отразить на диаграмме также состояние «оба генератора отказали», показатель надежности которого зависит от показателей надежности формирующих его состояний (например, является суммой вероятностей состояний).
В диаграммах состояний и переходов системы могут быть учтены стратегии технического обслуживания. Предположим, что существует только одна группа ремонтных рабочих и что стратегия технического обслуживания является такой, что приоритет ремонта всегда отдается компоненту, который отказал раньше. В этом случае должен учитываться порядок появления отказов. Такая диаграмма состояний изображена на рисунке 12.
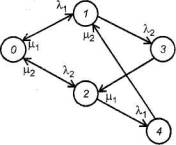
3 - два компонента отказали, первым отказал компонент 1; 4 - два компонента отказали, первым отказал компонент 2.
Рисунок 12 - Диаграмма состояний и переходов при наличии только одной группы ремонта
8 Оценки на основе диаграммы состояний и переходов
8.1 Общие положения
По диаграмме состояний и переходов может быть проведена оценка показателей надежности исследуемой системы с помощью математических методов. При этом определение таких величин как R(t) и A(t) требует значительно большего количества вычислений, чем определение установившихся величин, например таких, как MTTF, MDT, MUT и A(∞).
Оценку начинают с определения вероятностей обнаружения системы в конкретных состояниях. Вероятности, соответствующие отдельным состояниям, могут быть получены на основе матрицы переходов или путем решения дифференциальных уравнений в соответствии с приложением А.
Другие показатели надежности оценивают на основе этих вероятностей.
8.2 Оценка показателей надежности
Диаграмма состояний и переходов, используемая для оценки вероятности безотказной работы R(t), содержит, по крайней мере, одно состояние поглощения. Вероятность того, что система находится в данном состоянии в момент времени t, определяют при помощи специальных математических методов. Когда t стремится к бесконечности, вероятность, соответствующая каждому работоспособному состоянию, приближается к нулю, а вероятность состояний поглощения стремится к единице.
Распространенным показателем надежности является MTTFF. При оценке по диаграмме состояний и переходов MTTFF - среднее время пребывания системы в работоспособном состоянии до перехода в состояние поглощения.
8.3 Оценка показателей эффективности и ремонтопригодности
Диаграмма состояний и переходов, используемая для оценки коэффициентов готовности системы A(t) или А(∞), не содержит состояний поглощения.
Вероятность того, что система находится в данном состоянии в момент времени t, определяется методами, приведенными в приложении А. При t, стремящемся к бесконечности, вероятность, соответствующая каждому состоянию, стремится к постоянной величине. Коэффициент готовности системы также стремится к постоянной величине А(∞), так как он равен сумме вероятностей работоспособных состояний.
Кроме того, можно оценить две другие характеристики:
- среднее время пребывания системы в состоянии, которое является эквивалентом суммы интенсивностей перехода из этого состояния;
- частоту появления состояния, которая равна сумме Рu λu + Pvλv + ... где Рu и λu обозначают вероятность и интенсивность отказов, соответствующие состояниям u, v и т.д.
Примечание: Каждое слагаемое вида Рu λu соответствует переходу системы в смежное состояние, поэтому для определения частоты входа в состояние необходимо суммировать все такие слагаемые (см. раздел 9, пример).
Кроме того, на основе вероятностей состояний можно определить среднюю продолжительность работоспособного состояния системы (MUT) и среднее время простоя системы (MDT). MUT- фактическое среднее время пребывания в работоспособном состоянии, MDT- среднее время пребывания в неработоспособном состоянии. Также можно определить частоту появления неработоспособных состояний. Обычно это эквивалент интенсивности отказов системы (см. раздел 9, пример).
9 Упрощения и приближения
Во многих ситуациях среднее время восстановления элемента MTTR достаточно мало по сравнению с его MTTR, т.е. μ>> λ для всех элементов системы. Приближенное значение асимптотической вероятности Рi(∞) обнаружения системы в i-м состоянии, когда t стремится к бесконечности, можно легко определить. Метод основан на том, что если состояние «х» имеет один или большее количество переходов в неработоспособное состояние, искомая вероятность задается суммой Рu{∞), λu + Pv(∞)λv + ... , где Pv(∞), λv и другие члены суммы описаны в 8.3. Интенсивность переходов из этого состояния в состояние «х» обозначена Σμx. Тогда приближенная формула для Рx(∞) будет иметь следующий вид
![]()
где Рх(∞), Рu(∞) и Pv(∞) - асимптотические вероятности состояний.
Если эту процедуру повторить для каждого состояния, получим систему уравнений для вероятностей отдельных состояний. Необходимо отметить, что если для некоторых состояний системы переходы в состояние ремонта отсутствуют, то описанный приближенный метод не применим.
Описанный метод позволяет получить приближенное значение MTTFF системы. Для этого вычисляют все вероятности работоспособных состояний системы, которые затем используют для вычисления интенсивности отказов системы.
Пример - Рассмотрим диаграмму состояний и переходов, изображенную на рисунке 9. (Далее знак «∞» опущен). Все вероятности состояний являются постоянными. Величины Р1 и Р2 задаются уравнениями:
P1=λ1P0/μ1
Р2 = λ2P0/μ2
Таким образом, интенсивность отказов системы λs является частотой перехода системы в состояние отказа и задается соотношением
λS ≈ λ2P1 + λ1P2,
Таким образом, для μ >> λ, Ро ≈ 1
λs ≈ [λ2λ1/μ1 + λ1λ2/μ2]P0,
т.е. λs ≈ λ2 λ1/μ1 + λ1, λ2/μ2, так как μ>>λ и Р0 = 1.
Это выражение является известным. Его часто записывают в виде
λs≈λ1λ2[τ1 +τ2] ,
где τ - среднее время восстановления; τ1 ≈ 1/μ1, и τ2 ≈ 1/ μ2
10 Сокращенная диаграмма состояний и переходов
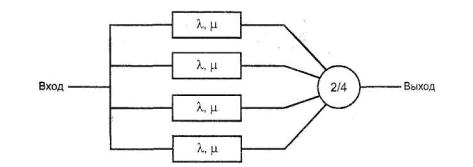
Рисунок 13 - Структурная схема надежности параллельной системы 2/4
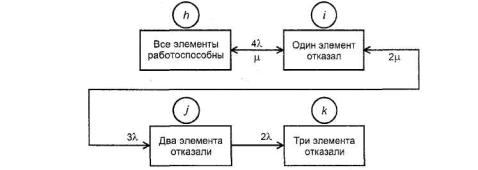
h, i, j - работоспособное состояние системы; к - неработоспособное состояние системы.
Рисунок 14 - Сокращенная диаграмма состояний и переходов для системы, изображенной на рисунке 13
Для упрощения вычислений диаграмма состояний и переходов должна включать как можно меньшее количество состояний. Если элементы зарезервированы и соединены параллельно, то все они имеют одинаковую интенсивность отказов λ и одинаковую интенсивность восстановлений μ, как показано на рисунке 13, и, если предполагается, что ремонтников столько, сколько необходимо, то диаграмма состояний и переходов может быть изображена в упрощенном виде, как показано на рисунке 14.
Решение системы линейных дифференциальных уравнений, соответствующих диаграмме, (см. приложение А), дает следующее выражение для определения средней наработки до первого отказа MTTFF:
![]()
Таким образом может быть получено точное выражение для определения MTTFF системы. Это выражение показывает способы получения формулы для сокращенных цепочек любой длины. Например для диаграммы, изображенной на рисунке 15,
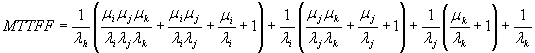

h, i, j, k - работоспособное состояние системы; 1 - неработоспособное состояние системы.
Рисунок 15 - Сокращенная диаграмма состояний и переходов для параллельной системы (четыре элемента)
11 Выражения для некоторых показателей надежности системы
Формулы для определения показателей надежности невосстанавливаемых систем приведены в таблице В.1 приложения В, а формулы для восстанавливаемых систем - в таблице В.2.
12 Представление результатов
Представление результатов должно включать, по меньшей мере, следующие элементы:
a) спецификацию показателей надежности (например, вероятность безотказности работы, коэффициент готовности, MTTF);
b) основные используемые предположения (например, постоянство интенсивности отказов и восстановлений);
c) определение выбранного метода;
d)описание диаграммы состояний и переходов, включая исследование следующих аспектов:
- отдельные описания работоспособных состояний и состояний отказа,
- по возможности, причины, по которым некоторые состояния сгруппированы, а другие не указаны,
- отдельное описание переходов между состояниями,
- выбор числовых значений для интенсивностей перехода,
- построенный путь диаграммы, включая любые предположения;
e) описание вычислений :
- методы,
- компьютерные программы (при их использовании);
f) числовые результаты:
- результаты в числовом виде и других формах,
- влияние предположений, используемых для построения диаграммы состояний и переходов или для вычислений;
- анализ чувствительности.
Приложение
А
(справочное)
Оценка некоторых показателей надежности системы, состоящей из двух элементов в нагруженном резерве
А.1 Цель
В качестве примера для определения оценки показателей надежности рассматривается система, состоящая из двух элементов, соединенных параллельно. Оцениваемые показатели - асимптотический коэффициент готовности, мгновенный коэффициент готовности, вероятность безотказной работы и MTTFF.
А.2 Моделирование
Диаграмма состояний и переходов системы изображена на рисунке А.1.
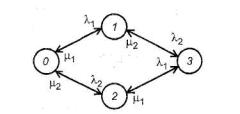
Рисунок А.1 - Диаграмма состояний и переходов для системы с двумя элементами
Диаграмму состояний и переходов для оценки вероятности безотказной работы R(t) получают из этой диаграммы путем устранения переходов восстановления от состояния 3 к состояниям 1 и 2. Состояние 3, таким образом, становится состоянием поглощения.
Предположим, что оба элемента в системе идентичны или имеют одинаковые интенсивности отказов/восстановлений. Сокращенная диаграмма изображена на рисунке А.2.
![]() .
.
Рисунок А.2 - Диаграмма состояний и переходов для параллельной системы, состоящей из двух идентичных элементов
Диаграмму состояний и переходов для оценки вероятности безотказной работы R(t) получают из этой диаграммы путем устранения перехода восстановлений от состояния 2 к состоянию 1. Состояние 2, таким образом, становится состоянием поглощения.
А.3 Метод дифференциальных уравнений
А.3.1 Метод для коэффициента готовности
Пусть P0(t), P1(t), P2(t) - вероятности пребывания системы в состояниях 0, 1 и 2, соответственно в момент времени t Следующие дифференциальные уравнения получены для диаграммы, изображенной на рисунке А.2:
![]()
![]()
![]()
При решении этой системы дифференциальных уравнений для вероятностей P0(t), P1(t), P2(t) предполагается, что в момент времени t = 0 система находится в состоянии 0, т.е:
Р0(0) = 1;
Р1(0) = 0.
Р2(0) = 0
В этом случае коэффициент готовности A(t) вычисляют по формуле:
A(t) = P0(t)+P1(t).
С помощью преобразования Лапласа можно получить это выражение через λ и μ
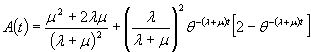
Из этого выражения вытекает выражение для определения асимптотического коэффициента готовности A(∞). Это выражение можно рассчитать иначе, если учесть, что в момент времени t = ∞ справедливы следующие равенства:
0 = 2λ Р0(∞) + μР1(∞);
0 = 2λ Р0(∞) - (λ + μ)Р1|(∞) + 2μP2(∞);
0 = λ Р1(∞) - 2μР2(∞);
Эти уравнения зависимы, так как любое уравнение может быть получено из двух других. В качестве третьего уравнения используют соотношение
Р0(∞) + Р1(∞)+Р2(∞) = 1.
В результате некоторых математических преобразований получаем формулу:
A(∞) = ![]()
А.3.2 Метод для вероятности безотказной работы
Для оценки вероятности безотказной работы и MTTFF системы, представленной на рисунке А.2, можно вывести следующие дифференциальные уравнения, предполагая, что состояние 2 является состоянием поглощения (переход восстановления из состояния 2 к состоянию 1 удален):
![]()
![]() (A.1)
(A.1)
![]()
Вероятности P(t), P1(t), P2(t) можно определить из системы дифференциальных уравнений (см. А.1), учитывая, что в момент времени t = 0 система находится в состоянии 0:
Р0(0) = 1;
Р1(0) = 0.
Р2(0) = 0
Таким образом, для вероятности безотказности работы RS справедливо уравнение
RS(t) = P0(t) + P1(t)
При помощи преобразования Лапласа можно получить выражение для RS через λ и μ
![]()
где для s1 ,s2 справедливы соотношения:
s1s2 =2λ2;
s1 + s2 = (μ + 3λ).
Выражение для MTTFF системы выводят либо из выражения для определения Rs(t)
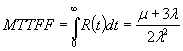
либо из системы уравнений, полученных интегрированием уравнений (см. А.1) в интервале от t = 0 до t = ∞
Приложение В (справочное)
Формулы для определения некоторых показателей надежности
Формулы для определения R(t) и MTTF невосстанавливаемых резервированных систем
|
Тип структуры |
R(t) |
MTTF |
|
1
из n |
|
|
|
1 из n |
1-(1-р)n |
|
|
(n - 1) из n |
npn-1-(n-1)pn |
|
|
2 из 3 |
Зр2-2р3 |
|
|
2 из 4 |
6р2-8р3 + 3р4 |
|
|
3 из 5 |
10р3-15р4 + 6р5 |
|
|
r из n |
|
|
|
1
из n |
|
|
|
r из n |
- |
|
|
Р = е-λt |
||
Приближенные формулы для определения интенсивности отказов восстанавливаемых параллельных систем
|
Тип структуры |
Тип резервирования |
Средняя интенсивность отказов |
|
1 из n (общая формула) |
а |
|
|
(n - 1) из n |
а |
|
|
(n - 1) из n |
а |
|
|
1 из 2 |
а |
|
|
1 из 3 |
а |
|
|
2 из 3 |
а |
|
|
1 из 2 |
а |
|
|
(n - 1) из n |
s |
|
|
Примечания: 1 Обозначения типа резервирования: а - нагруженный резерв; s - ненагруженный резерв, 2 Предположения: 1) ремонтных рабочих столько, сколько необходимо; 2) идеальный переключатель; 3) λμ < < 1. |
||
Ключевые слова: риск, менеджмент риска, анализ надежности, показатели надежности, вероятность безотказной работы, коэффициент готовности, интенсивность отказов, интенсивность восстановлений.