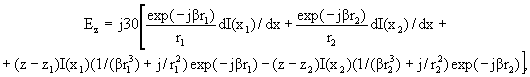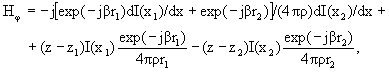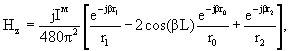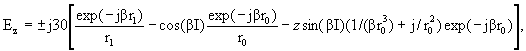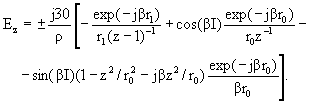ГОСУДАРСТВЕННАЯ СИСТЕМА
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКОГО
НОРМИРОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
4.3. МЕТОДЫ КОНТРОЛЯ. ФИЗИЧЕСКИЕ ФАКТОРЫ
ОПРЕДЕЛЕНИЕ
УРОВНЕЙ
ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
НА РАБОЧИХ МЕСТАХ ПЕРСОНАЛА
РАДИОПРЕДПРИЯТИЙ, ТЕХНИЧЕСКИЕ
СРЕДСТВА КОТОРЫХ РАБОТАЮТ
В НЧ, СЧ И ВЧ ДИАПАЗОНАХ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
МУК 4.3.677-97
Минздрав России
Москва
1998
1. Разработаны Бузовым А.Л., Романовым В.А., Казанским Л.С., Кольчугиным Ю.И., Юдиным В.В. (Самарский отраслевой научно-исследовательский институт радио Министерства связи Российской Федерации).
2. Представлены Госкомсвязи России письмом от 27.05.97 № НТУОТ-1/058. Одобрены Комиссией по государственному санитарно-эпидемиологическому нормированию при Минздраве России.
3. Утверждены и введены в действие Главным государственным санитарным врачом Российской Федерации от 6 ноября 1997 г.
4. Введены впервые.
СОДЕРЖАНИЕ
«УТВЕРЖДАЮ»
Главный государственный
санитарный врач Российской Федерации
Г.Г. Онищенко
06 ноября 1997 г.
МУК 4.3.677-97
Дата введения: с момента утверждения.
4.3. МЕТОДЫ КОНТРОЛЯ. ФИЗИЧЕСКИЕ ФАКТОРЫ
ОПРЕДЕЛЕНИЕ
УРОВНЕЙ
ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
НА РАБОЧИХ МЕСТАХ ПЕРСОНАЛА
РАДИОПРЕДПРИЯТИЙ, ТЕХНИЧЕСКИЕ
СРЕДСТВА КОТОРЫХ РАБОТАЮТ
В НЧ, СЧ И ВЧ ДИАПАЗОНАХ
Методические указания
1. ОБЛАСТЬ ПРИМЕНЕНИЯ
Методические указания составлены в помощь инженерам органов и учреждений санитарно-эпидемиологической службы, инженерно-техническим работникам, проектным организациям средств связи с целью обеспечения предупредительного санитарного надзора за источниками излучения кило- (НЧ), гекто- (СЧ) и декаметрового (ВЧ) диапазонов на предприятиях радиовещания и радиосвязи, а также для прогнозирования уровней напряженности электромагнитного поля при организации рабочих мест обслуживающего персонала.
2. СУЩНОСТЬ МЕТОДА
Методы контроля уровней электромагнитных полей на рабочих местах персонала радиопредприятий НЧ, СЧ и ВЧ диапазонов содержат метод расчетного прогнозирования напряженности электромагнитного поля излучающих технических средств радиосвязи и радиовещания в кило-, гекто- и декаметровом диапазонах волн, а также методику измерений уровней электромагнитного поля. Расчетные и экспериментальные исследования, производимые в соответствии с данной методикой, являются необходимыми и достаточными при проведении электромагнитной экспертизы излучающих объектов.
Метод расчетного прогнозирования электромагнитных полей на рабочих местах персонала, обслуживающего технические средства НЧ, СЧ и ВЧ диапазонов базируется на строгих решениях соответствующих электродинамических задач тонкопроволочных структур, при известных функциях распределения токов по излучателям, которые определяются на основе приближенных решений.
Методические указания распространяются на радиотехнические объекты, которые могут быть укомплектованы как техническими средствами одного частотного диапазона, так и техническими средствами различных частотных диапазонов. Электромагнитные поля технических средств могут отличаться интенсивностью, поляризацией, частотами, зависимостью от параметров почвы и т.д. Методические указания учитывают индивидуальность реальных объектов, проявляющуюся (с точки зрения электромагнитной обстановки) в различии размещения и ориентации отдельных источников излучения, в несовпадении расписаний смены волн, в неодинаковом наборе технических средств.
К основным источникам электромагнитного поля внутри технических зданий на рабочих местах обслуживающего персонала относятся:
- экраны бикоаксиальных фидеров передатчиков с симметричным выходом;
- экраны коаксиальных фидеров передатчиков с несимметричным выходом;
- щели шкафов передатчиков;
- антенны радиоцентра. В расчетном прогнозировании электромагнитное поле определяется для конкретных электрофизических моделей технических помещений с учетом тех или иных источников излучения.
3. ОСНОВНЫЕ ПОЛОЖЕНИЯ МЕТОДИКИ РАСЧЕТНОГО ПРОГНОЗИРОВАНИЯ
Особенностью электромагнитного прогнозирования в НЧ, СЧ и ВЧ диапазонах является то, что поле необходимо определять в ближней зоне излучения. При этом напряженность поля определяется как суперпозиция полей источников излучения и вторичных полей, создаваемых токами, наведенными этими источниками (т.е. первичным полем) на металлические поверхности помещений (каркасы и обшивка шкафов передатчиков, трубы водяного охлаждения, внешние поверхности экранов коаксиальных и бикоаксиальных внутренних фидеров и т.п.).
Учесть эти факторы возможно только решением соответствующей электродинамической задачи, в рамках которой находятся наведенные токи.
3.1. ИЗЛУЧЕНИЕ ИСТОЧНИКОВ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Первичное поле источников излучения рассчитывается поэтапно. В качестве сторонних источников рассматриваются поля, создаваемые токами на внешних поверхностях экранов фидеров, излучением из щелей шкафов передатчиков, а в случае неэкранированного здания - излучением антенн радиоцентра. Расчет токов экранов фидеров выполняется на основе теории длинных линий; волновые сопротивления эквивалентных линий, образованных экранами и шинами заземления, находятся путем решения двумерной электростатической задачи; в качестве возбуждающих источников рассматриваются вертикальные участки шин заземления в сечении перехода на наружный фидер, обладающие конечным индуктивным сопротивлением и возбуждающиеся за счет асимметрии тока передатчиков с симметричным выходом или за счет недостаточного экранирующего действия проволочного экрана наружного концентрического фидера передатчика с несимметричным выходом. Излучение щелей шкафов рассматривается как действие эквивалентных магнитных токов, текущих вдоль щелей. Поля, создаваемые излучением антенн рассчитываются методом, учитывающим реальные электрофизические параметры подстилающей поверхности.
3.1.1. ИЗЛУЧЕНИЕ ЭКРАНОВ БИКОАКСИАЛЬНЫХ ФИДЕРОВ ПЕРЕДАТЧИКОВ С СИММЕТРИЧНЫМ ВЫХОДОМ
Расчет поля, создаваемого излучением бикоаксиальных фидеров, выполняется за 5 этапов:
1) расчет геометрических параметров эквивалентной линии (ЭЛ), одним проводом которой является экран фидера, другим - шина заземления;
2) расчет параметров ЭЛ - волновых сопротивлений однородных участков и импедансов в сечениях стыков этих участков определенных в сторону передатчика;
3) расчет параметров выходной цепи ЭЛ (вертикальный участок шины заземления, антенный фидер) и напряжения на выходе ЭЛ, т.е. в сечении перехода на наружный концентрический фидер;
4) расчет тока ЭЛ на каждом однородном участке;
5) расчет поля, создаваемого этим током ЭЛ.
На первом этапе вводится декартова система координат таким образом, чтобы плоскость (XOY) совпадала с плоскостью земли. Азимутальная ориентация осей (OX) и (OY) может быть произвольной. Данная основная система является общей для всех фидеров и других элементов здания и используется впоследствии при всех расчетах. Фидер представляется каскадным соединением однородных отрезков ЭЛ. Из соображений унификации каждый однородный отрезок должен быть прямолинейным, т.е. его длина не должна превышать длину участка фидера между соседними поворотами. В тех случаях, когда в пределах прямолинейного участка имеется резкое изменение однородности ЭЛ (скачкообразное изменение расстояния между фидером и шиной), можно разделить этот участок на два или более однородных отрезка. Каждый однородный отрезок характеризуется декартовыми координатами его крайних точек. Для определенности точки берутся на экране фидера (а не на шине). Координаты должны образовывать упорядоченную пару векторов, очередность записи которых определяет положительное направление тока на данном отрезке (1-й вектор - начало отрезка, 2-й - конец). Определение пространственного положения отрезков ЭЛ необходимо для расчета создаваемого ее током поля.
На втором этапе выполняется расчет волновых сопротивлений ЭЛ путем решения двумерной электростатической задачи методом интегрального уравнения, которое в свою очередь решается методом моментов.
Волновое сопротивление линии передачи полностью определяются ее погонной емкостью Сс, Ф/м, которая характеризует электростатическую связь между проводами линии, т.е. определяет величину погонного заряда провода при некоторой разности потенциалов проводов в соответствии с соотношениями:
Q1 = Сл(φ1 - φ2), Q2 = Сл(φ2 - φ1), (3.1)
где Q1 и Q2 - соответственно погонные заряды провода 1 и провода 2, Кл/м, причем Q2 = -Q1 (для определенности считается, что провод 1 - экран фидера, провод 2 - шина заземления);
φ1 и φ2 - соответственно потенциалы провода 1 и провода 2, В.
Для определения погонной емкости Сл достаточно решить следующую электростатическую задачу: потенциал провода 1 φ1 задать равным, например, 1 В, потенциал провода 2 положить равным нулю, т.е. φ2 = 0 и найти погонные заряды проводов. Тогда из (3.1) находится емкость по формуле:
Сл = |Qл|/Δφ, (3.2)
где Qл - погонный заряд одного из проводников (безразлично какого), Кл/м;
Δφ = |φ1 - φ2| - абсолютное значение разности потенциалов, В.
При решении электростатической задачи о нахождении погонных зарядов проводов линии целесообразно использовать интегральное уравнение (являющееся решением известного дифференциального уравнения Пуассона):
где ρ - плотность заряда, Кл/м3;
ε0 - электрическая постоянная;
где v и v` - радиусы-векторы точек пространства (v - точка наблюдения; v` - переменная интегрирования);
r - расстояние между точками v и v`.
Поскольку заряд существует только на поверхности проводников, объемный интеграл можно заменить соответствующим поверхностным (при этом плотность заряда ρ является поверхностной, Кл/м2, в поперечном сечении относительно оси линии она будет функцией криволинейной координаты, отсчитываемой вдоль контура поперечного сечения проводника; вдоль линии - константой). Далее, поскольку потенциалы точек, лежащих на поверхности проводников известны, левую часть (3.3) можно рассматривать как заданную функцию. При таком подходе выражение (3.3) является уравнением Фредгольма 1-го рода.
Линия полагается бесконечно протяженной (в обе стороны от исследуемого сечения). Сплошные поверхности проводников заменяются равномерно заряженными полосками нулевой толщины, протяженность которых (в продольном направлении) много больше поперечных размеров линии (что соответствует ее бесконечной протяженности). Дискретное распределение заряда по полоскам является приближенным аналогом непрерывного распределения плотности заряда по сплошным поверхностям. Особенность в интегральном уравнении, имеющая место при v → v`, исключается тем, что в случае распределения заряда по поверхности величина заряда в точке v` (т.е. на бесконечно малой площадке, содержащей точку v, в которой вычисляется потенциал) стремится к нулю.
Выражения для потенциалов полосок образуют систему уравнений, которая в матричной записи имеет вид:
где [P] - комплексная матрица потенциальных коэффициентов размерностью М ´ М, каждый элемент которой P^ представляет собой коэффициент при заряде j-й полоски q^ - интеграл в (3.3), взятый по поверхности j-й полоски, подынтегральная функция которого определяется i-й и j-й полосками с учетом того, что за знак интеграла вынесена искомая функция (т.е. в подынтегральной функции q(v`) = 1 Кл); [q] - вектор-столбец погонных зарядов полосок, Кл/м; [φ] - вектор-столбец потенциалов полосок, В. Решением системы (3.4) находятся погонные заряды полосок.
Полные погонные заряды проводников находятся как соответствующие суммы зарядов образующих их полосок.
Учет влияния полупроводящей земли в методе моментов может быть осуществлен введением зеркальных изображений полосок. Эквивалентные погонные заряды зеркальных изображений полностью определяются погонными зарядами соответствующих полосок, поэтому размер матрицы /P/ в (3.4) остается при этом неизменным (к каждому элементу Pij добавляется составляющая потенциала, создаваемая на i-й полоске зеркальным изображением j-й полоски).
Волновые сопротивления однородных участков находятся по формуле
wj = 1/(C0qj) (3.5)
где C0 скорость света в воздухе.
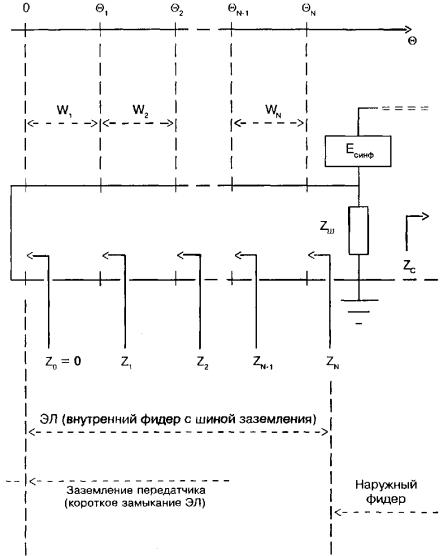
После нахождения волновых сопротивлений однородных участков полностью восстанавливается схема ЭЛ, которая показана на рис. 1. Линия состоит из N каскадно включенных участков. Каждый i-й участок характеризуется волновым сопротивлением Wi и координатой своего конца, которая представляет собой электрическое расстояние от передатчика Θi (электрическая длина i-го отрезка - есть разность Θi - Θi-1). На схеме использованы обозначения: Z1, Z2, …, ZN - входные импедансы отрезков; Zш - импеданс вертикального участка шины заземления; Zc - входной импеданс наружного фидера по однотактной волне; Eсинф - напряжение синфазной волны на выходе внутреннего фидера.
Входные импедансы отрезков находятся по рекуррентной формуле:
Z1 = jW1tg(Θ1), ![]() (3.6)
(3.6)
i = 1, 2, …, N.
На третьем этапе рассчитываются импеданс вертикального участка шины заземления Zш, входной импеданс наружного фидера по однотактной волне Zc и напряжение на выходе ЭЛ un (см. рис. 1).
Импеданс вертикального участка шины заземления Zш рассчитывается по формуле:
Zш = jωLш, (3.7)
где ω - круговая частота, рад/с;
Lш - индуктивность шины, Гн.
Схема эквивалентной линии, образованной экраном внутреннего фидера и шиной заземления
Рис. 1
Индуктивность шины Lш следует рассчитывать по формуле
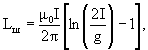
где μ0 - магнитная проницаемость воздуха;
I - длина шины;
g - величина, значение которой находится по формуле
![]()
где c - ширина шины;
K и E - полные эллиптические интегралы первого и второго рода с модулем k, определяемые из уравнения
![]()
где K', E' - полные эллиптические интегралы с дополнительным модулем
![]()
b - толщина шины.
Для расчета волнового сопротивления наружного фидера по однотактной волне (т.е. величины Zc) используется тот же метод, что и для нахождения волновых сопротивлений однородных участков.
Для оценки величины Eсинф используется нормируемый показатель - максимально допустимая асимметрия токов на выходе двухтактного каскада, т.е. предполагается, передатчик исправен. Амплитудное значение Eсинф принимается равным 2 … 3 % от амплитудного значения противофазной составляющей напряжения при 100 % модуляции.
Цепь на выходе ЭЛ (см. рис. 1) представляет собой делитель напряжения, одним плечом которого является импеданс Zc, другое образовано параллельным соединением Zш и ZN. Следовательно, напряжение в сечении ЭЛ Θ = ΘN определяется соотношением:
![]() (3.8)
(3.8)
Далее, на четвертом этапе, находится ток ЭЛ. Для этого в пределах каждого i-го однородного отрезка вводятся амплитуды падающей Ui и отраженной Vi волн напряжения, отнесенные ко входному сечению данного отрезка (так что имеет место равенство Ui + Vi = ui-1). Величины Ui и Vi находятся из условия выполнения закона Ома во входном сечении и непрерывности напряжения в ЭЛ как функции Θ. Опуская громоздкие промежуточные выкладки запишем рекуррентные соотношения для Ui, Vi и напряжений ui в сечениях Θ1, Θ2, … Θi, … ΘN-1 (напряжение un уже найдено):
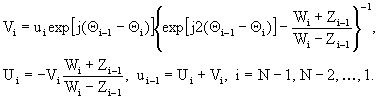 (3.9)
(3.9)
Ток i-го отрезка при этом определяется выражением:
![]() (3.10)
(3.10)
Таким образом, на первых четырех этапах находится распределение тока по каждому однородному отрезку ЭЛ.
Пятый этап. Выражения для составляющих поля Ez, Eρ, Hφ, создаваемых прямолинейным кусочно-синусоидальным током в некоторой точке наблюдения с координатами ρ, z в цилиндрической системе координат, ось аппликат которой совпадает с линией тока и направлена в соответствии с его положительным направлением:
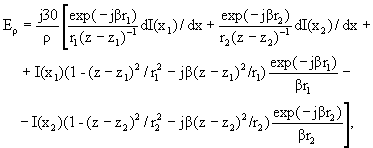 (3.12)
(3.12)
где z1 и z2 - аппликаты начала и конца данного прямолинейного однородного отрезка ЭЛ, соответственно;
r1 и r2 - расстояние до точки наблюдения от начала и конца отрезка, соответственно;
I(x) - токовая функция;
x - криволинейная координата - расстояние до передатчика по фидеру;
x1 и x2 - координаты x начала и конца отрезка, соответственно.
Аналогичным образом находится поле, создаваемое током шины (равным по модулю и противоположным по фазе току экрана фидера).
3.1.2. ИЗЛУЧЕНИЕ ЭКРАНОВ КОАКСИАЛЬНЫХ ФИДЕРОВ ПЕРЕДАТЧИКОВ С НЕСИММЕТРИЧНЫМ ВЫХОДОМ
Поле, создаваемое током коаксиального фидера передатчика с несимметричным выходом рассчитывается как и в случае бикоаксиального фидера за пять этапов. Процедура расчета отличается только третьим этапом, т.е. иначе рассчитываются параметры выходной цепи ЭЛ и ее выходное напряжение.
Рассмотрим третий этап для коаксиального фидера. В данном случае обратный ток частично течет по проволочному экрану концентрического фидера, частично - по земле. Мерой удельного веса тока земли в общем обратном токе является коэффициент прозрачности проволочного экрана kп. Суммарный обратный ток перетекает на внутреннюю поверхность экрана коаксиального фидера передатчика с проволочного экрана, шины заземления и внешней своей поверхности. Последняя составляющая и есть ток ЭЛ. В эквивалентной схеме ток земли течет по параллельному соединению импедансов Zш (вертикальный участок шины) и ZN (входной импеданс последнего N-го однородного отрезка ЭЛ, - см. рис. 1).
При расчете тока земли сначала находится коэффициент прозрачности проволочного экрана k формуле:
kп = 1 - C12/C11, (3.14)
где C12 - взаимная погонная емкость между центральным проводом и проволочным экраном концентрического фидера;
C11 - собственная емкость центрального провода.
Емкости C11 и C12 находятся решением электростатической задачи (методом, описанным в предыдущем пункте) при потенциале центрального провода фидера 1 В и при нулевых потенциалах проволочного экрана и земли: величины C11 и C12 при этом совпадают с абсолютными значениями погонных зарядов центрального проводника и экрана, соответственно. Затем вычисляется ток земли Iз формуле:
Iз = kпI0, (3.15)
где I0 - ток центрального провода, который находится как выходной ток передатчика в предположении высокого уровня согласования антенны.
Напряжение на выходе ЭЛ un рассчитывается как падение напряжения на параллельном соединении Zш и ZN при протекании тока Iз:
un = Iз/(1/Zш + 1/ZN). (3.16)
В остальном, как уже отмечалось выше, расчет аналогичен случаю бикоаксиального фидера передатчика с симметричным выходом.
3.1.3. ИЗЛУЧЕНИЕ ЩЕЛЕЙ ШКАФОВ ПЕРЕДАТЧИКОВ
Щели шкафов передатчиков рассматриваются как короткие магнитные вибраторы, возбужденные кусочно-синусоидальным эквивалентным магнитным током щели с амплитудой в пучности Iм. На основе принципа перестановочной двойственности уравнений Максвелла получены замкнутые выражения для φ-составляющей электрического, ρ- и z-составляющих магнитного полей в цилиндрической системе координат, ось аппликат которой совпадает с осью вибратора, начало координат - с его центром:
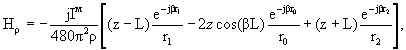 (3.18)
(3.18)
где r1, r0, r2 - расстояния до точки наблюдения от разных точек вибратора, определяемых подстрочными индексами:
- индекс «2» - начало (нижняя крайняя точка в данной системе координат);
- индекс «0» - центр (средняя точка);
- индекс «1» - конец (верхняя крайняя точка).
Для определения величины Iм используется формула (3.19), при этом считается, что величина Eφ задана. Возможны два случая:
- в ТУ на передатчики данного типа установлено требование для максимально допустимой напряженности с указанием расстояния от стенки передатчика, на котором это требование проверяется;
- в ТУ на передатчики данного типа упомянутое требование установлено либо без указания расстояния, на котором оно проверяется, либо в виде ссылки на ПДУ.
В первом случае имеются все необходимые исходные данные для вычисления эквивалентного магнитного тока щели. Во втором случае предлагается, руководствуясь величинами напряженности поля, взятыми из ТУ или (при отсутствии в ТУ) из гигиенического норматива, считать что эти значения определены на расстоянии 0,3 … 0,7 м от стенки передатчика. Тем или иным способом определенная напряженность Eφ подставляется в (3.19), в результате из этого выражения находится амплитуда эквивалентного магнитного тока в пучности Iм.
3.1.4. ИЗЛУЧЕНИЕ АНТЕНН РАДИОЦЕНТРА
Расчет поля, создаваемого излучающими антеннами радиоцентров, подробно приведен в «Методических указаниях МУК 4.3.044-96. Определение уровней электромагнитного поля, границ санитарно-защитной зоны и зон ограничения застройки в местах размещения передающих средств радиовещания и радиосвязи кило-, гекто- и декаметрового диапазонов».
3.2. РАСЧЕТ ТОКОВ, НАВЕДЕННЫХ НА МЕТАЛЛИЧЕСКИЕ ЭЛЕМЕНТЫ
Расчет токов, наведенных на металлические элементы, проводится следующим образом.
Задача решается как дифракционная методом интегрального уравнения в тонкопроволочном приближении (задача о рассеянии стороннего поля). Объект представляется как система «тонких» проводов - проволочная модель. Большинство металлических элементов внутри здания реально являются линейными проводниками (экраны фидеров, трубы водяного охлаждения, шины заземления и т.д.), экранированные стены и железобетонные перекрытия моделируются как сплошные металлические поверхности проволочными сетками. Для решения интегрального уравнения использован известный метод сшивания в дискретных точках при кусочно-синусоидальном базисе разложения токовой функции. В разделе подробно описаны основные вычислительные процедуры, выполняемые в рамках метода.
3.2.1. МЕТОД ИНТЕГРАЛЬНОГО УРАВНЕНИЯ В ТОНКОПРОВОЛОЧНОМ ПРИБЛИЖЕНИИ
Поля, создаваемые источниками, рассмотренными выше, имели бы место при отсутствии других металлических предметов. В данном случае электромагнитное поле будет подвержено влиянию проводящих (экранированных) стен здания, фидеров, шин заземления, труб водяного охлаждения, шкафов передатчиков и т.д. В результате действия источников на этих предметах наведутся токи, которые в свою очередь вызовут появление поля рассеяния. Результирующее поле будет суперпозицией первичного поля рассмотренных выше источников и вторичного - поля рассеяния на металлических телах, расположенных в здании. Первичное поле следует рассматривать как стороннее, при этом необходимо находить вторичный ток на экранах фидеров, который в сумме с первичным (найденным при моделировании этих источников) представляет реальную картину распределения тока с учетом взаимодействия фидеров между собой и с другими проводниками.
В качестве исходного интегрального уравнения используется уравнение Харрингтона. Его решение выполняется методом сшивания в точках при кусочно-синусоидальном базисе разложения токовой функции. В предыдущем подразделе подробно рассмотрены связанные с этим теоретические вопросы. Ниже дается описание конкретных вычислительных процедур.
3.2.2. МЕТОД СШИВАНИЯ В ТОЧКАХ ПРИ КУСОЧНО-СИНУСОИДАЛЬНОМ БАЗИСЕ
Решение задачи о рассеянии поля сторонних источников в здании (т.е. о наведенных токах) выполняется за 4 этапа:
1) построение тонкопроволочной модели;
2) построение на проводах сегментов с кусочно-синусоидальными базисными функциями;
3) расчет коэффициентов и свободных членов системы линейных алгебраических уравнений (СЛАУ) - аналога исходного интегрального уравнения;
4) решение СЛАУ, в результате чего находятся амплитуды токов сегментов в пучностях - коэффициенты при базисных функциях, которые совместно с последними полностью восстанавливают функцию, аппроксимирующую истинное распределение тока.
Проволочная модель представляет собой систему прямолинейных проводников. Она должна включать:
- все линейные проводники (фидеры, трубы водяного охлаждения и т.д.);
- шкафы передатчиков (в диапазонах НЧ и СЧ шкафы с превалирующим размером моделируются одним проводом большого радиуса, в диапазоне ВЧ - проволочной сеткой);
- экранированные стены и перекрытия здания (в том числе железобетонные).
Модель строится в основной декартовой системе, использованной при моделировании источников. Каждый прямолинейный проводник задается упорядоченной парой радиус-векторов крайних точек (порядок записи векторов определяет положительное направление тока). Линейные размеры ячеек сеток, моделирующих сплошные поверхности, не должны превышать 3,5 % длины волны, и быть, по крайней мере, вдвое меньше расстояния до ближайшего линейного проводника (например, фидера). С целью снижения объема вычислений следует варьировать густоту сетки в зависимости от расстояния до линейных проводников, шкафов передатчиков и др. В случае сложной конфигурации здания можно разделить объект на отдельные части, соединенные электрически малыми дверными проемами, и для каждой такой части отдельно решать задачу.
Система проводников модели представляет собой криволинейный контур L`. Для определения базисных функций на нем выделяются N коротких отрезков - сегментов. Каждый k-й сегмент определяется тремя точками: I`1,k - начало, I`0,k - средняя точка, I`2,k - конец. Соответствующая ему k-я базисная функция задается выражениями:
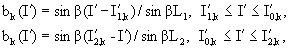 (3.20)
(3.20)
где L1 = I`0,k - I`1,k;
L2 = I`2,k - I`0,k.
В сущности, сегмент представляет собой короткий вибратор с кусочно-синусоидальным током, причем в общем случае его плечи - отрезки [I`1,k, I`0,k] и [I`0,k, I`2,k] - могут не лежать на одной прямой и иметь разную длину. Соседние сегменты частично перекрываются: средняя точка k-го сегмента I`0,k совпадает с концом (k - 1)-го и началом (k + 1)-го сегментов.
Электрические контакты между проводниками (например, в узлах сетки) описываются введением специальных сегментов, плечи каждого из которых лежат на разных проводниках. При этом автоматически выполняется закон Кирхгоффа для узла цепи.
На поверхности провода на расстоянии его радиуса у средней точки каждого сегмента вводится соответствующая точка сшивания. Кривые, соединяющие точки сшивания и проходящие по поверхности проводников образуют контур L.
Токовая функция представляется в виде разложения по системе базисных функций:
![]() (3.22)
(3.22)
где Ik - неизвестные (искомые) коэффициенты - амплитуды токов сегментов в пучностях.
Величины Ik находятся решением СЛАУ:
где каждый коэффициент Zik выражает связь между k-м и i-м сегментами и имеет смысл тангенциальной составляющей поля в точке сшивания i-го сегмента при Ik = 1 А, свободные члены Ei обусловлены действием сторонних источников. Коэффициенты Zik вычисляются следующим образом. Поскольку плечи сегмента в общем случае могут не лежать на одной прямой, удобно вычислять поле каждого плеча отдельно, суммируя затем соответствующие тангенциальные составляющие. Поле, создаваемое одним плечом, целесообразно вычислять в виде разложения по единичным векторам 1z и 1ρ цилиндрической системы координат, ось аппликат которой (OZ) совмещена с плечом, средняя точка сегмента находится в начале координат, начало (для 1-го плеча) или конец (для 2-го плеча) сегмента находится в области положительных z.
Формулы для z-й и ρ-й компонент поля, создаваемого в точке сшивания одним из плеч сегмента (в соответствующей цилиндрической системе) имеют вид:
где r1 - расстояние до точки наблюдения от начала (конца) сегмента, м;
r0 - расстояние до точки наблюдения от средней точки сегмента, м;
β = 2π/λ - волновое число;
λ - длина волны, м;
l - длина рассматриваемого плеча, м;
z и ρ - цилиндрические координаты точки наблюдения (соответственно аппликата и проекция радиус-вектора точки на плоскость z = 0, м).
Знак «+» в (3.24, 3.25) соответствует 1-му плечу сегмента, знак «-» - 2-му.
Пусть z- и ρ-компоненты поля по формулам (3.24, 3.25) рассчитаны для обоих плеч k-го сегмента, т.е. получены 4 числа. Обозначим их Em,k, m = 1, 2, 3, 4. Каждой m-й компоненте в исходной основной системе координат соответствует единичный вектор 1`m,k. С учетом этих обозначений формула для Zik может быть записана в виде:
![]() (3.26)
(3.26)
где 1i - единичный вектор, тангенциальный к L в i-й точке сшивания.
Формула для свободных членов Ei имеет вид:
Ei = j(1i, Eст(vi)), (3.27)
где Eст(vi) - стороннее поле, создаваемое всеми источниками рассмотренными выше;
vi - радиус-вектор i-й точки сшивания в исходной основной системе координат.
После вычисления коэффициентов и свободных членов составляется и решается СЛАУ (3.23).
Решение СЛАУ наиболее целесообразно выполнять методом оптимального исключения, требующим сохранения в памяти ЭВМ только верхней треугольной матрицы коэффициентов СЛАУ (включая главную диагональ) и столбца свободных членов.
3.3. РАСЧЕТ УРОВНЕЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
После решения СЛАУ (3.23) имеем систему токов:
- сторонние на экранах фидеров и эквивалентные магнитные токи щелей шкафов передатчиков;
- наведенные на металлические тела, в том числе на экраны фидеров, обтекаемые сторонними токами (полный ток экранов фидеров будет суммой сторонних и наведенных токов).
Кроме того (в случае неэкранированного здания) имеются сторонние поля создаваемые антеннам радиоцентра.
Полное поле в некоторой точке наблюдения будет суперпозицией стороннего поля антенн, поля сторонних токов (экраны фидеров, щели шкафов) и поля наведенных токов.
Электрическое поле излучения антенн находится методом, описанным выше. Для вычисления магнитного поля можно, учитывая удаленность антенн, использовать приближенный подход, основанный на предположении о волновом характере поля. При этом для антенны вертикальной поляризации в цилиндрической системе (ось аппликат вертикальна и совпадает с антенной) магнитное поле имеет только φ-составляющую:
Hφ = Ez/(120π), (3.28)
для антенны горизонтальной поляризации в такой же цилиндрической системе надо найти Eφ, тогда магнитное поле будет иметь только z-составляющую:
Hz = Eφ/(120π). (3.29)
Поле, создаваемое сторонними токами экранов фидеров, вычисляется по формулам (3.11 - 3.13), как это было описано выше; поле излучения из щелей шкафов передатчиков - по формулам (3.17 - 3.19).
Поле, создаваемое наведенными токами является суперпозицией полей отдельных сегментов. Для вычисления электрического поля необходимо методом, описанным выше, рассчитать коэффициенты СЛАУ для точки наблюдения, рассматривая ее как точку сшивания, причем контур L поочередно ориентировать вдоль базисных векторов основной декартовой системы. Тогда поле одного сегмента (пусть это будет i-й сегмент) будет произведением тока в пучности Ii на этот коэффициент.
Магнитное поле сегментов вычисляется как суперпозиция полей отдельных их плеч следующим образом. Для каждого плеча каждого сегмента строится цилиндрическая система координат так, что ось аппликат (OZ) совпадает с плечом, центральная точка сегмента находится в начале координат, его крайняя точка - в области положительных z. В такой системе магнитное поле будет иметь только φ-составляющую, которая вычисляется по формуле:
![]() (3.30)
(3.30)
где I0 - ток в пучности, т.е. коэффициент Ii для i-го сегмента, найденный в результате решения СЛАУ;
r1 и r0 - расстояния до точки наблюдения от крайней и средней точки сегмента, соответственно;
I - длина плеча;
z и ρ - цилиндрические координаты точки наблюдения. После вычисления Hφ для некоторого плеча, находятся проекции вектора магнитного поля на оси основной декартовой системы. Данная процедура выполняется для всех плеч, полное магнитное поле наведенных токов находится как сумма соответствующих проекций.
4. МЕТОДИКА ИЗМЕРЕНИЯ УРОВНЕЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Инструментальный контроль уровней ЭМП проводится с целью определения фактического состояния электромагнитной обстановки на рабочих местах обслуживающего персонала и служит средством оценки достоверности результатов расчета. Измерения проводятся:
- на этапе предупредительного санитарного надзора - при приемке радиотехнического объекта (РТО) в эксплуатацию;
- на этапе текущего санитарного надзора - при изменении технических характеристик или режимов работы (мощности излучения, антенно-фидерного тракта, направлений излучения и т.п.);
- при изменении ситуационных условий размещения технических средств станций (изменение расположения антенн, фидеров, высот их установки, азимута или угла места максимального излучения антенн, изменения расположения передатчиков);
- после проведения защитных мероприятий, направленных на снижение уровней ЭМП;
- в порядке плановых контрольных измерений (не реже одного раза в год).
При подготовке к проведению измерений проводятся следующие работы:
- согласование с заинтересованными предприятиями и организациями цели, времени и условий проведения измерений;
- определение необходимости использования средств индивидуальной защиты;
- подготовка необходимой измерительной аппаратуры. Настоящая методика распространяется на все рабочие места персонала радиопредприятий, излучающих энергию НЧ, СЧ и ВЧ диапазонов.
4.1. ОПЕРАЦИИ ИЗМЕРЕНИЙ
При проведении измерений должны выполняться следующие операции:
- измерение напряженности электрической составляющей электромагнитного поля.
- измерение напряженности магнитной составляющей электромагнитного поля.
- пересчет измеренных уровней электрической и магнитной составляющих в значения энергетической нагрузки.
4.2. СРЕДСТВА ИЗМЕРЕНИЯ
При проведении измерений должны применяться следующие образцовые и вспомогательные средства:
- селективный микровольтметр SMV-11 (SMV-6);
- специальная антенна для измерения электрической составляющей ЭМП на частотах 0,06 - 30 МГц («ОРТ»);
- специальная антенна для измерения магнитной составляющей ЭМП на частотах 0,06 - 30 МГц.
Разрешается, кроме указанных выше, применять другие измерительные селективные (WMS-4, ESH 2, ESH 3, ESHS 10) и широкополосные приборы (NFM-1, ПЗ-15 - ПЗ-22) с погрешностями не хуже, чем у приборов, перечисленных выше.
4.3. УСЛОВИЯ ИЗМЕРЕНИЙ
При проведении измерений должны соблюдаться следующие условия:
- температура окружающей среды 293 ± 5 К° (20 ± 5 С°);
- атмосферное давление 100 ± 4 кПа (750 ± 30 мм. рт. ст.);
- относительная влажность воздуха 65 ± 15 %;
- напряжение питания сети частотой 50 Гц ± 1 % и содержание гармоник до 5 % должно быть 220 В ± 2 %.
Измерения на рабочих местах проводят на расстояниях от источников ЭМП, соответствующих нахождению тела работающих, на нескольких уровнях от поверхности пола или земли с определением максимального значения напряженности ЭМП для каждого рабочего места.
Минимальное расстояние между измерительной антенной и металлическими поверхностями не должно быть менее четырех максимальных размеров антенны, при размерах антенны не более 0,25 м.
4.4. ПРОВЕДЕНИЕ ИЗМЕРЕНИЙ
4.4.1.1. Уровень напряженности поля определяют на каждой рабочей частоте радиопередающего устройства.
4.4.1.2. Включают селективный микровольтметр и прогревают его в течение времени, указанном в инструкции по эксплуатации.
4.4.1.3. Специальную антенну для измерения электрической составляющей ЭМП располагают в выбранной плоскости XOY по оси X в соответствующей точке измерения.
4.4.1.4. Включают (если оно не работает) радиопередающее устройство в режим непрерывного излучения.
4.4.1.5. Устанавливают и калибруют частоту прибора SMV-11.
4.4.1.6. Настраивают прибор на измеряемый сигнал.
4.4.1.7. Проводят калибровку усиления.
4.4.1.8. Отсчитывают измеренное значение напряжения по сумме ослабления на делителях и по показанию индикаторного прибора в дБ.
4.4.1.9. Определяют напряженность поля по сумме измеренного значения напряжения и калибровочного коэффициента специальной измерительной антенны на данной частоте в дБ.
4.4.1.10. Производят пересчет значения напряженности поля Ex, выраженной в дБ относительно 1 мкВ, в В/м по формуле
Ex (В/м) = 100,05Е(дБ)×10-6.
4.4.1.11. Ориентируют измерительную антенну по оси Y, повторяют действия по пп. 4.4.1.7 - 4.4.1.10, определяя Ey.
4.4.1.12. Устанавливают измерительную антенну ортогонально к плоскости XOY, повторяют действия по пп. 4.4.1.7 - 4.4.1.10, определяя Ez.
4.4.1.13. Повторяют измерения составляющих Ex, Ey, Ez еще два раза. Выбирают наибольшие из измеренных значений.
4.4.1.14. Повторяют действия по пп. 4.4.1.7 - 4.4.1.13, поместив антенну в другую точку пространства на рабочем месте обслуживающего персонала (на другую высоту). Выбирают наибольшие из измеренных значений.
4.4.1.15. Повторяют действие по п. 4.4.1.14 так, чтобы на одном рабочем месте были проведены измерения не менее, чем в трех точках. Выбирают наибольшие из измеренных значений.
4.4.1.16. Производят пересчет измеренных значений в значение суммарной составляющей по формуле
![]() .
.
4.4.2. Измерение уровня напряженности магнитной составляющей ЭМП в диапазоне частот 0,06 - 30 МГц.
4.4.2.1. Измерения проводят согласно п. 4.4.1, заменив антенну для измерения электрической составляющей на специальную антенну для измерения магнитной составляющей.
4.4.2.2. Производят пересчет измеренных значений в значение суммарной составляющей по формуле
![]() .
.
4.4.3. Проводят измерения электрической и магнитной составляющих ЭМП, создаваемого другими радиопередающими устройствами на их рабочих частотах согласно пп. 4.4.1 - 4.4.2.
Результаты измерений оформляются протоколом.