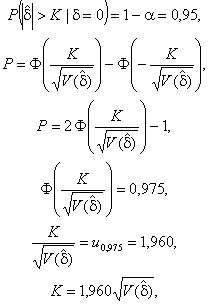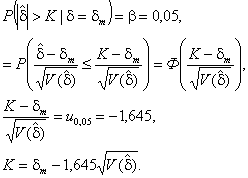ГОСТ Р ИСО 5725-4-2002
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ
И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ
И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Часть 4
Основные методы определения правильности
стандартного метода измерений
ГОССТАНДАРТ РОССИИ
Москва
Предисловие
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологической службы» Госстандарта России (ВНИИМС), Всероссийским научно-исследовательским институтом стандартизации (ВНИИСтандарт), Всероссийским научно-исследовательским институтом классификации, терминологии и информации по стандартизации и качеству (ВНИИКИ) Госстандарта России
ВНЕСЕН Управлением метрологии и Научно-техническим управлением Госстандарта России
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 23 апреля 2002 г. № 161-ст
3 Настоящий стандарт представляет собой полный аутентичный текст международного стандарта ИСО 5725-4:1994 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений»
4 ВВЕДЕН ВПЕРВЫЕ
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ К ГОСУДАРСТВЕННЫМ СТАНДАРТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002 ПОД ОБЩИМ ЗАГОЛОВКОМ «ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ»
Целью разработки государственных стандартов Российской Федерации ГОСТ Р ИСО 5725-1-2002, ГОСТ Р ИСО 5725-2-2002, ГОСТ Р ИСО 5725-3-2002, ГОСТ Р ИСО 5725-4-2002, ГОСТ Р ИСО 5725-5-2002, ГОСТ Р ИСО 5725-6-2002, далее - ГОСТ Р ИСО 5725, является прямое применение в Российской Федерации шести частей основополагающего Международного стандарта ИСО 5725 под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений» в практической деятельности по метрологии (разработке, аттестации и применению методик выполнения измерений), стандартизации методов контроля (испытаний, измерений, анализа), испытаниям продукции, в том числе для целей подтверждения соответствия, оценке компетентности испытательных лабораторий согласно требованиям ГОСТ Р ИСО/МЭК 17025-2000.
ГОСТ Р ИСО 5725 представляют собой полный аутентичный текст шести частей международного стандарта ИСО 5725, в том числе:
ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения»;
ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»;
ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений»;
ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике».
Каждая часть содержит аутентичный перевод предисловия и введения к международному стандарту ИСО 5725, а также предисловие к государственным стандартам Российской Федерации (ГОСТ Р ИСО 5725-1-2002 - ГОСТ Р ИСО 5725-6-2002) и издается самостоятельно.
Пользование частями 2 - 6 ГОСТ Р ИСО 5725 в отдельности возможно только совместно с частью 1 (ГОСТ Р ИСО 5725-1), в которой установлены основные положения и определения, касающиеся всех частей ГОСТ Р ИСО 5725.
В соответствии с основными положениями ИСО 5725-1 (пункт 1.2) настоящий стандарт распространяется на методы измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающие в качестве результата измерений единственное значение. При этом это единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
Стандарты ИСО 5725 могут применяться для оценки точности выполнения измерений различных физических величин, характеризующих измеряемые свойства того или иного объекта, в соответствии со стандартизованной процедурой. При этом в пункте 1.2 ИСО 5725-1 особо отмечено, что стандарт может применяться для оценки точности выполнения измерений состава и свойств очень широкой номенклатуры материалов, включая жидкости, порошкообразные и твердые материалы - продукты материального производства или существующие в природе, при условии, что учитывают любую неоднородность материала.
Применяемый в международных стандартах термин «стандартный метод измерений» адекватен отечественному термину «стандартизованный метод измерений».
В ИСО 5725: 1994 - 1998 и ИСО/МЭК 17025-99 понятие «метод измерений» («measurement method») включает совокупность операций и правил, выполнение которых обеспечивает получение результатов с известной точностью. Таким образом, понятие «метод измерений» по ИСО 5725 и ИСО/МЭК 17025 адекватно понятию «методика выполнения измерений (МВИ)» по ГОСТ Р 8.563-96 «Государственная система обеспечения единства измерений. Методики выполнения измерений» (пункт 3.1) и соответственно значительно шире по смыслу, чем определение термина «метод измерений» в Рекомендации по межгосударственной стандартизации РМГ 29-99 «Государственная система обеспечения единства измерений. Метрология. Основные термины и определения» (пункт 7.2).
Более того, в оригинале ИСО 5725 очень часто употребляется в качестве понятия «метод измерений» и английский термин «test method», перевод которого на русский язык - «метод испытаний» (см. примечание 1 к пункту 3.2 ИСО 5725-1) и который по смыслу совпадает с термином 6.2 ИСО 5725-1 «standard measurement method» (стандартизованный метод измерений). Соответственно в качестве термина «результат измерений» в оригинале стандарта чаще используется английский термин «test result» (см. пункт 3.2 ИСО 5725-1), причем в контексте как с термином «test method» (см. пункт 3.2), так и с термином «measurement method» (см. в оригинале, например, пункты 1.2 или 7.2.1 ИСО 5725-1).
При этом следует иметь в виду, что область применения ИСО 5725 - точность стандартизованных методов измерений, в том числе предназначенных для целей испытаний продукции, позволяющих количественно оценить характеристики свойств (показателей качества и безопасности) объекта испытаний (продукции). Именно поэтому во всех частях стандарта результаты измерений характеристик образцов, взятых в качестве выборки из партии изделий (или проб, отобранных из партии материала), являются основой для получения результатов испытаний всей партии (объекта испытаний). Когда объектом испытаний является конкретный образец (test speciment, sample), результаты измерений и испытаний могут совпадать. Такой подход имеет место в примерах по определению показателей точности стандартного (стандартизованного) метода измерений, содержащихся в ИСО 5725.
Следует отметить, что в отечественной метрологии точность (accuracy) и погрешность (error) результатов измерений, как правило, определяются сравнением результата измерений с истинным или действительным (условно истинным) значением измеряемой физической величины (являющимися фактически эталонными значениями измеряемых величин, выраженными в узаконенных единицах).
В условиях отсутствия необходимых эталонов, обеспечивающих воспроизведение, хранение и передачу соответствующих значений единиц величин, необходимых для оценки погрешности (точности) результатов измерений, и в отечественной, и в международной практике за действительное значение зачастую принимают общее среднее значение (математическое ожидание) установленной (заданной) совокупности результатов измерений. В ИСО 5725 эта ситуация отражена в термине «принятое опорное значение» (см. пункты 3.5 и 3.6 ГОСТ Р ИСО 5725-1) и рекомендуется ГОСТ Р ИСО 5725-1 для использования в этих случаях и в отечественной практике.
Термины «правильность» (trueness) и «прецизионность» (precision) в отечественных нормативных документах по метрологии до настоящего времени не использовались. При этом «правильность» - степень близости результата измерений к истинному или условно истинному (действительному) значению измеряемой величины или в случае отсутствия эталона измеряемой величины - степень близости среднего значения, полученного на основании большой серии результатов измерений (или результатов испытаний) к принятому опорному значению. Показателем правильности обычно является значение систематической погрешности (см. пункт 3.7 ГОСТ Р ИСО 5725-1).
В свою очередь «прецизионность» - степень близости друг к другу независимых результатов измерений, полученных в конкретных установленных условиях. Эта характеристика зависит только от случайных факторов и не связана с истинным или условно истинным значением измеряемой величины (см. пункт 3.12 ГОСТ Р ИСО 5725-1). Мера прецизионности обычно вычисляется как стандартное (среднеквадратическое) отклонение результатов измерений, выполненных в определенных условиях. Количественные значения мер прецизионности существенно зависят от заданных условий. Экстремальные показатели прецизионности - повторяемость, сходимость (repeatability) и воспроизводимость (reproducibility) регламентируют и в отечественных нормативных документах, в том числе в большинстве государственных стандартов на методы контроля (испытаний, измерений, анализа) (см. пункты 3.12 - 3.20 ГОСТ Р ИСО 5725-1).
В соответствии с ИСО 5725 цель государственных стандартов ГОСТ Р ИСО 5725 состоит в том, чтобы:
а) изложить основные положения, которые следует иметь в виду при оценке точности (правильности и прецизионности) методов и результатов измерений при их применении, а также при планировании экспериментов по оценке различных показателей точности (ГОСТ Р ИСО 5725-1);
б) регламентировать основной способ экспериментальной оценки повторяемости (сходимости) и воспроизводимости методов и результатов измерений (ГОСТ Р ИСО 5725-2);
в) регламентировать процедуру получения промежуточных показателей прецизионности методов и результатов измерений, изложив условия их применения и методы оценки (ГОСТ Р ИСО 5725-3);
г) регламентировать основные способы определения правильности методов и результатов измерений (ГОСТ Р ИСО 5725-4);
д) регламентировать для применения в определенных обстоятельствах несколько альтернатив основным способам (ГОСТ Р ИСО 5725-2 и ГОСТ Р ИСО 5725-4) определения прецизионности и правильности методов и результатов измерений, приведенных в ГОСТ Р ИСО 5725-5;
е) изложить некоторые практические применения показателей правильности и прецизионности (ГОСТ Р ИСО 5725-6).
Представленные в виде таблицы рекомендации по применению основных положений ГОСТ Р ИСО 5725 в деятельности по метрологии, стандартизации, испытаниям, оценке компетентности испытательных лабораторий со ссылками на нормы государственных стандартов Российской Федерации, содержащих требования к выполнению соответствующих работ, приведены в приложении к предисловию в ГОСТ Р ИСО 5725-1.
Алгоритмы проведения экспериментов по оценке повторяемости, воспроизводимости, промежуточных показателей прецизионности, показателей правильности (характеристик систематической погрешности) методов и результатов измерений рекомендуется внедрять через программы экспериментальных метрологических исследований показателей точности (характеристик погрешности) результатов измерений, выполняемых по разрабатываемой МВИ, и (или) через программы контроля показателей точности применяемых МВИ.
Использование приведенных в приложениях А к каждому стандарту условных обозначений в качестве обязательных рекомендуется только для тех показателей точности, которые до настоящего времени в отечественной метрологической практике не использовались (например, для показателей по пунктам 3.9 - 3.12 ГОСТ Р ИСО 5725-1). Для остальных показателей и критериев используемые в ГОСТ Р ИСО 5725 условные обозначения, как правило, могут применяться наряду с условными обозначениями этих показателей и критериев, принятых в действующих отечественных документах (например, предел повторяемости (сходимости) с условным обозначением r по пункту 3.16 ГОСТ Р ИСО 5725-1 наряду с условным обозначением d, принятым для этого показателя в ряде рекомендаций по метрологии, а также в государственных стандартах на методы испытаний продукции).
ПРЕДИСЛОВИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
Международная организация по стандартизации (ИСО) является Всемирной федерацией национальных организаций по стандартизации (комитетов - членов ИСО). Разработка международных стандартов обычно осуществляется техническими комитетами ИСО. Каждый член ИСО, заинтересованный в деятельности соответствующего технического комитета, имеет право быть представленным в этом комитете. Правительственные и неправительственные международные организации, сотрудничающие с ИСО, также принимают участие в этой работе. ИСО тесно сотрудничает с Международной электротехнической комиссией (МЭК) по всем вопросам стандартизации в области электротехники.
Проекты международных стандартов, принятые техническими комитетами, направляются техническим комитетам - членам ИСО на голосование перед их утверждением Советом ИСО в качестве международных стандартов. Стандарты утверждаются в качестве международных в соответствии с установленными в ИСО требованиями: в случае их одобрения по меньшей мере 75 % комитетов - членов ИСО, принимавших участие в голосовании.
Международный стандарт ИСО 5725-4 был подготовлен Техническим комитетом ИСО/ТК 69 «Применение статистических методов», Подкомитетом ПК 6 «Методы и результаты измерений».
ИСО 5725 состоит из следующих частей под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений»:
Часть 1. Основные положения и определения
Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
Часть 4. Основные методы определения правильности стандартного метода измерений
Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
Часть 6. Использование значений точности на практике
ИСО 5725 (части 1 - 6) в совокупности аннулирует и заменяет ИСО 5725:1986, область распространения которого была расширена включением правильности (в дополнение к прецизионности) и условий промежуточной прецизионности (в дополнение к условиям повторяемости и воспроизводимости).
Приложение А является обязательным для настоящей части стандарта ИСО 5725, приложения В, С и D - справочные.
ВВЕДЕНИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
0.1 В ИСО 5725 для описания точности метода измерений используются два термина: «правильность» и «прецизионность». Термин «правильность» характеризует степень близости среднего арифметического значения большого числа результатов измерений к истинному или принятому опорному значению, термин «прецизионность» - степень близости результатов измерений друг к другу.
0.2 Общие положения об этих понятиях представлены в ИСО 5725-1 и поэтому здесь не повторяются. Эта часть ИСО 5725 должна читаться в сочетании с ИСО 5725-1, поскольку в ней даны определения и общие положения.
0.3 Правильность метода измерений имеет смысл в тех случаях, когда можно получить представление об истинном значении измеряемой характеристики (свойства). Хотя для некоторых методов измерений истинное значение измеряемой величины точно неизвестно, возможно получение ее опорного значения, например, когда имеются в распоряжении соответствующие стандартные образцы1 или когда принятое опорное значение может быть установлено сличением с другим методом измерений или приготовленным образцом известного состава. При этом правильность метода измерений можно исследовать сопоставлением принятого опорного значения измеряемой величины с уровнем результатов измерений, полученных этим методом. Правильность, как правило, выражается термином «систематическая погрешность». Например, в химическом анализе систематическая погрешность появляется в случаях, когда метод измерений не позволяет полностью извлечь элемент или когда наличие одного элемента влияет на определение другого.
1 Термин «стандартные образцы (СО)» в ИСО 5725 и ИСО/МЭК 17025 соответствует английскому термину «reference materials (RM)»; в необходимых случаях в тексте оригинала ИСО 5725-4, ИСО 5725-6 и ИСО/МЭК 17025 (пункт 5.6.3.2) используют термин «certified reference materials (CRM)», что в переводе на русский язык означает «аттестованные стандартные образцы» (см., например, пункт 4.2.1 ГОСТ Р ИСО 5725-4). В ГОСТ Р ИСО 5725, а также в ГОСТ Р ИСО/МЭК 17025-2000 этот термин (CRM) используют применительно к государственным и отраслевым стандартным образцам (ГСО и ОСО) по ГОСТ 8.315-97. Термин «стандартные образцы предприятия (лаборатории) (СОП)» соответствует английскому термину «internal reference materials» или «private reference materials prepared by the laboratory»; последнее словосочетание переводится как «собственные стандартные образцы, приготовленные лабораторией» (см., например, пункт 6.2.2.1с ИСО 5725-6).
0.4 В настоящей части стандарта ИСО 5725 рассматриваются две меры правильности.
a) Систематическая погрешность метода1: если метод измерений может дать увеличение смещенного значения измеряемой величины, сохраняющееся независимо от того, где и когда выполнялось измерение, то представляет интерес установить «систематическую погрешность метода измерений» (согласно определению, данному в ИСО 5725-1). Это требует проведения эксперимента, охватывающего много лабораторий, как описано в ИСО 5725-2.
b) Систематическая погрешность лаборатории1: измерения в пределах одной лаборатории могут обнаруживать «лабораторную систематическую погрешность» (согласно определению, данному в ИСО 5725-1) (при реализации конкретного метода измерений). Если для ее оценки проводят эксперимент, он должен быть осуществлен так, чтобы оценка была действительна только на момент его проведения. Чтобы доказать, что систематическая погрешность лаборатории при реализации конкретного метода измерений не меняется во времени, требуется проведение дальнейших регулярных измерений; для этой цели можно использовать метод, описанный в ИСО 5725-6.
1 Соответствующие определения даны в пунктах 3.7-3.10 ГОСТ Р ИСО 5725-1.
ГОСТ Р ИСО 5725-4-2002
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Часть 4
Основные методы определения правильности стандартного метода измерений
Accuracy (trueness and precision) of measurement methods and results. Part 4. Basic methods for the determination of the trueness of a standard measurement method
Дата введения 2002-11-01
1 Область применения
1.1 Настоящий стандарт описывает основные способы оценки систематической погрешности метода измерений и систематической погрешности результатов измерений в лаборатории при его реализации.
1.2 Настоящий стандарт относится исключительно к методам измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающим в качестве результата измерений единственное значение. При этом это единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
1.3 Чтобы измерения выполнялись по единой процедуре, важно, чтобы метод измерений был стандартизован. Все измерения необходимо выполнять согласно стандартному методу.
1.4 Количественные оценки значений систематической погрешности отражают возможности метода измерений давать корректный (истинный) результат. Когда значение систематической погрешности метода измерений приводится совместно с результатом измерений, полученным данным методом, то подразумевают, что одни и те же характеристики измеряют строго одинаковым образом.
1.5 Настоящий стандарт может применяться лишь в случае, если принятое опорное значение может быть установлено в качестве условно истинного значения, например с применением эталонов или соответствующих стандартных образцов, либо ссылкой на эталонный метод измерений, либо приготовлением образца известного состава.
Стандартными образцами могли бы быть:
a) аттестованные стандартные образцы;
b) материалы с известными свойствами, подготовленные для проведения эксперимента;
c) материалы, свойства которых были установлены путем измерений альтернативным методом, известным тем, что его систематическая погрешность пренебрежимо мала.
1.6 В настоящем стандарте рассматривают только случаи, когда достаточно оценить систематическую погрешность на одном уровне измеряемой характеристики в данное время. Это не применимо в случаях, когда систематическая погрешность при измерении одной характеристики подвержена влиянию уровня второй характеристики (то есть не рассматриваются взаимные влияния).
Сопоставление правильности двух методов измерений рассматривается в ГОСТ Р ИСО 5725-6.
Примечание 1 - Поскольку в настоящем стандарте систематическую погрешность рассматривают только на одном уровне в данное время, индекс j для уровня опускают.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Общие положения и определения
ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
3 Определения
В настоящем стандарте применяют термины с определениями, представленные в ИСО 3534-1 [1] и в ГОСТ Р ИСО 5725-1.
Условные обозначения и сокращения, используемые в ГОСТ Р ИСО 5725, представлены в приложении А.
4 Определение систематической погрешности стандартного метода измерений посредством межлабораторного эксперимента
4.1 Статистическая модель
В базовой модели, описанной в 5.1 ГОСТ Р ИСО 5725-1, общее среднее значение m может быть заменено на
m = m + d, (1)
где m - принятое опорное значение измеряемой характеристики;
d - систематическая погрешность метода измерений.
Модель принимает следующий вид
y = m + d + B + e. (2)
Равенство (2) используют в случае, когда интерес представляет d. Здесь B представляет собой лабораторную составляющую систематической погрешности стандартного метода измерений, то есть составляющую результата измерений, представляющую межлабораторную вариацию.
Систематическую погрешность лаборатории D представляют следующим выражением
D = d + B, (3)
поэтому модель может быть записана в виде
y = m + D + e. (4)
Равенство (4) используют в случае, когда интерес представляет А.
4.2 Требования к стандартному образцу
В случае использования стандартных образцов должны удовлетворяться требования, приведенные в 4.2.1 и 4.2.2. Стандартные образцы должны быть гомогенными.
4.2.1 Выбор стандартных образцов
4.2.1.1 Стандартный образец должен иметь известные характеристики, соответствующие уровню измеряемой характеристики, на котором предполагается применить стандартный метод измерений, например, уровню концентрации. В некоторых случаях важно будет включить в оценочный эксперимент серию стандартных образцов, каждый из которых соответствует отличному от другого уровню характеристики, поскольку систематические погрешности стандартного метода измерений могут быть различными на разных уровнях. Стандартный образец должен иметь матрицу, как можно более близкую к матрице материала, испытуемого стандартным методом измерений, например углерод в угле или углерод в стали.
4.2.1.2 Количество стандартного образца должно быть достаточным для выполнения полной программы эксперимента, включая некоторый резерв, если это будет признано необходимым.
4.2.1.3 Стандартный образец должен иметь стабильные характеристики в течение всего эксперимента. Имеют место три случая:
a) характеристики стабильны - в каких бы то ни было мерах предосторожности нет необходимости;
b) аттестованное значение характеристики может изменяться в зависимости от условий хранения: контейнер должен храниться как до, так и после его открытия таким образом, как это описано в аттестате на стандартный образец;
c) характеристики изменяются во времени по известному закону: представляется аттестат, содержащий аттестованное значение характеристики, установленное в определенное время.
4.2.1.4 Возможное различие между аттестованным и истинным значением, выраженное через неопределенность стандартного образца (см. Руководство ИСО 35 [2]), в методах, приводимых в настоящем стандарте, не принимают во внимание.
4.2.2 Проверка и распределение стандартного образца
В случаях, когда перед распределением происходит разделение единицы стандартного образца, это должно выполняться осторожно, чтобы избежать внесения какой-либо дополнительной погрешности. Для справок следует воспользоваться соответствующими международными стандартами по разделению (разделу) проб. Единицы стандартных образцов для распределения должны отбираться по случайному принципу. Если имеет место неразрушающий измерительный контроль, возможно предоставить всем лабораториям, участвующим в межлабораторном эксперименте, одну и ту же единицу стандартного образца, однако это увеличит продолжительность эксперимента.
4.3 Основные требования к схемам организации эксперимента по оценке систематической погрешности метода измерений
4.3.1 Целью эксперимента является оценка значения систематической погрешности метода измерений и установление, является ли она статистически значимой. Если установлено, что систематическая погрешность не является статистически значимой, то целью является определение значения максимальной систематической погрешности, которая могла бы, с определенной вероятностью, оставаться необнаруживаемой в результатах эксперимента.
4.3.2 Программа эксперимента - аналогична программе эксперимента по оценке прецизионности, описанного в 4.1 ГОСТ Р ИСО 5725-2. Различия заключаются в следующем:
a) существует дополнительное требование к использованию принятого опорного значения и
b) количество участвующих лабораторий и число результатов измерений должны также удовлетворять требованиям 4.5.
4.4 Ссылки на ГОСТ Р ИСО 5725-1 и ГОСТ Р ИСО 5725-2
Используют раздел 6 ГОСТ Р ИСО 5725-1 и разделы 5 и 6 ГОСТ Р ИСО 5725-2. При чтении частей 1 и 2 ГОСТ Р ИСО 5725 в контексте части 4 вместо терминов «прецизионность» или «повторяемость и воспроизводимость» следует употреблять термин «правильность».
4.5 Необходимое количество лабораторий
Количество лабораторий и результатов измерений, требующихся на каждом уровне, взаимозависимы. Необходимое количество лабораторий рассматривают в 6.3 ГОСТ Р ИСО 5725-1. Указания в отношении их количества, приведены ниже.
Для того, чтобы в результате эксперимента можно было достаточно надежно оценить систематическую погрешность метода (см. приложение С), минимальное количество лабораторий p и результатов измерений n должно удовлетворять следующему неравенству
где dm - заданное значение систематической погрешности, которое участник эксперимента желает обнаружить в результатах эксперимента;
sR - стандартное отклонение воспроизводимости метода измерений.
А как функция р и п задается следующим выражением
где g = sR/sr; (7)
sr - стандартное отклонение повторяемости метода измерений.
Значения А представлены в таблице 1.
В идеальном случае выбор сочетания количества лабораторий и повторно получаемых результатов измерений на лабораторию должен удовлетворять требованию, описанному уравнением (5) при значении dm, задаваемом экспериментатором. Однако из практических соображений выбор количества лабораторий обычно представляет собой компромисс между наличием ресурсов и желанием снизить значение dm до удовлетворительного уровня. Если воспроизводимость метода измерений невысока, то тогда практически невозможно будет достигнуть высокой степени определенности при оценке систематической погрешности. Когда sR > sr (то есть g > 1), как это часто происходит, получением более чем двух результатов измерений на лабораторию из расчета на уровень мало чего можно достичь.
Таблица 1 - Значения неопределенности оценки систематической погрешности метода измерений
|
g = 1 |
g = 2 |
g = 5 |
|||||||
|
n = 2 |
n = 3 |
n = 4 |
n = 2 |
n = 3 |
n = 4 |
n = 2 |
n = 3 |
n = 4 |
|
|
5 |
0,62 |
0,51 |
0,44 |
0,82 |
0,80 |
0,79 |
0,87 |
0,86 |
0,86 |
|
10 |
0,44 |
0,36 |
0,31 |
0,58 |
0,57 |
0,56 |
0,61 |
0,61 |
0,61 |
|
15 |
0,36 |
0,29 |
0,25 |
0,47 |
0,46 |
0,46 |
0,50 |
0,50 |
0,50 |
|
20 |
0,31 |
0,25 |
0,22 |
0,41 |
0,40 |
0,40 |
0,43 |
0,43 |
0,43 |
|
25 |
0,28 |
0,23 |
0,20 |
0,37 |
0,36 |
0,35 |
0,39 |
0,39 |
0,39 |
|
30 |
0,25 |
0,21 |
0,18 |
0,33 |
0,33 |
0,32 |
0,35 |
0,35 |
0,35 |
|
35 |
0,23 |
0,19 |
0,17 |
0,31 |
0,30 |
0,30 |
0,33 |
0,33 |
0,33 |
|
40 |
0,22 |
0,18 |
0,15 |
0,29 |
0,28 |
0,28 |
0,31 |
0,31 |
0,31 |
4.6 Статистическая оценка
Результаты измерений должны быть обработаны согласно ГОСТ Р ИСО 5725-2. В частности, если выявляются выбросы, должны быть предприняты необходимые меры, чтобы изучить причины их появления, включая переоценку соответствия принятого опорного значения.
4.7 Интерпретация результатов статистической оценки
4.7.1 Проверка прецизионности
Прецизионность метода измерений выражают через sr (оценку стандартного отклонения повторяемости) и sr (оценку стандартного отклонения воспроизводимости). В равенствах (8) - (10) принято допущение, заключающееся в равном количестве (n) результатов измерений в каждой лаборатории. Если это условие не соблюдается, то для расчета sr и sr должны быть использованы соответствующие формулы, приведенные в ГОСТ Р ИСО 5725-2.
4.7.1.1 Оценку sr2 дисперсии повторяемости для p участвующих в эксперименте лабораторий рассчитывают следующим образом
![]() (9)
(9)
где si2 и ![]() - соответственно дисперсия и среднее
значение n результатов измерений yik, полученных в
лаборатории i.
- соответственно дисперсия и среднее
значение n результатов измерений yik, полученных в
лаборатории i.
Для подтверждения, что между внутрилабораторными дисперсиями не существует никаких существенных различий, к дисперсиям si2 необходимо применить критерий Кохрена, описанный в ГОСТ Р ИСО 5725-2. С целью более тщательного исследования потенциальных выбросов должны быть также построены диаграммы Манделя h и k, приведенные в ГОСТ Р ИСО 5725-2.
Если стандартное отклонение повторяемости стандартного метода измерений ранее не было определено в соответствии с ГОСТ Р ИСО 5725-2, то sr будет считаться его наилучшей оценкой. Если стандартное отклонение повторяемости sr стандартного метода было определено в соответствии с ГОСТ Р ИСО 5725-2, то значение дисперсии sr2 может быть оценено следующим соотношением
![]() (11)
(11)
Статистику C сравнивают с критическим значением
![]()
где ![]() представляет собой (1
- a)-квантиль c2-распределения с
n[ = p(n - 1)] степенями
свободы. Если не установлено иначе, то a принимают равным 0,05.
представляет собой (1
- a)-квантиль c2-распределения с
n[ = p(n - 1)] степенями
свободы. Если не установлено иначе, то a принимают равным 0,05.
a) Если C £ Ccrit, то sr2 не значимо больше sr2.
b) Если C > Ccrit, то sr2 значимо больше sr2.
В первом случае для оценки систематической погрешности метода измерений будет использовано стандартное отклонение повторяемости sr. В последнем случае необходимо исследовать причины расхождения и, возможно, повторить эксперимент.
4.7.1.2 Оценку sR2 дисперсии воспроизводимости для p участвующих в эксперименте лабораторий рассчитывают следующим образом
![]() (12)
(12)
![]() (13)
(13)
Если стандартное отклонение воспроизводимости стандартного метода измерений ранее не было определено в соответствии с ГОСТ Р ИСО 5725-2, то sR будет его наилучшей оценкой. Если стандартные отклонения воспроизводимости sR и повторяемости sr стандартного метода измерений были определены в соответствии с ГОСТ Р ИСО 5725-2, то sr может быть косвенно оценено путем вычисления следующего соотношения
![]() (14)
(14)
Статистику C¢ сравнивают с критическим значением
![]()
где ![]() представляет собой (1
- a)-квантиль c2-распределения с
n [ = p - 1] степенями
свободы. Если не установлено иначе, то a принимают равным 0,05.
представляет собой (1
- a)-квантиль c2-распределения с
n [ = p - 1] степенями
свободы. Если не установлено иначе, то a принимают равным 0,05.
a) Если C¢ £ Ccrit, то sR2 - (1 - 1/n)sr2 не значимо больше sR2 - (1 - 1/n)sr2.
b) Если C¢ > Ccrit, то sR2 - (1 - 1/n)sr2 значимо больше sR2 - (1 - 1/n)sr2.
В первом случае для оценки правильности метода измерений будут использованы стандартные отклонения повторяемости sr и воспроизводимости sR. В последнем случае перед оценкой систематической погрешности стандартного метода измерений должно быть произведено тщательное исследование рабочих условий выполнения измерений в каждой лаборатории. Может оказаться, что некоторые лаборатории не пользовались требуемым оборудованием либо не работали в заданных условиях. При химическом анализе трудности могут возникнуть, например, из-за недостаточного контроля в лаборатории температуры, влажности окружающего воздуха, наличия в воздухе загрязняющих веществ и т.д. В результате для получения ожидаемых значений прецизионности может оказаться необходимым повторить эксперимент.
4.7.2 Оценка систематической погрешности стандартного метода измерений
Оценку систематической погрешности, полученной при оценке компетентности лабораторий, выражают равенством
![]() (15)
(15)
где ![]() может быть
положительным или отрицательным.
может быть
положительным или отрицательным.
Если абсолютная величина оцениваемой систематической погрешности меньше или равна половине ширины интервала неопределенности, установленной в соответствии с Руководством ИСО 35 [2], то нет оснований говорить о наличии систематической погрешности.
Вариация оценки систематической погрешности метода измерений является следствием изменчивости результатов измерительного процесса и выражается как стандартное отклонение, определяемое следующим образом
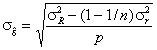 (16)
(16)
в случае известных значений прецизионности, или
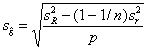 (17)
(17)
в случае неизвестных значений прецизионности.
Приближенно 95 %-ный доверительный интервал для систематической погрешности метода измерений может быть рассчитан следующим образом
![]() (18)
(18)
где А определяется равенством (6).
Если значение sR неизвестно, то вместо него должна быть использована его оценка sr, и A должно быть рассчитано при g = sR/sr.
Если доверительный интервал включает в себя нулевое значение, систематическая погрешность метода измерений при уровне значимости a = 5 % незначима; в противном случае ее следует считать значимой.
5 Определение систематической погрешности лаборатории при реализации стандартного метода измерений
Как будет описано ниже, эксперименты одной лаборатории используют для оценки систематической погрешности лаборатории (при реализации конкретного стандартного метода измерений) при условии, что в результате межлабораторного эксперимента по оценке прецизионности, в соответствии с ГОСТ Р ИСО 5725-2, было установлено стандартное отклонение повторяемости метода.
5.1 Выполнение эксперимента
Эксперимент должен строго соответствовать стандартному методу, а измерения должны выполняться в условиях повторяемости. Перед оценкой правильности нужно проверить прецизионность при реализации лабораторией стандартного метода измерений. Это подразумевает сопоставление внутрилабораторного стандартного отклонения с установленным стандартным отклонением повторяемости метода.
Программа эксперимента включает измерения, требуемые от одной лаборатории в эксперименте по оценке прецизионности, описанном в ГОСТ Р ИСО 5725-2. Помимо ограничения до одной лаборатории, единственным существенным различием является дополнительное требование использования принятого опорного значения.
При попытке измерить систематическую погрешность результатов лаборатории при реализации стандартного метода измерений могут оказаться не заслуживающими внимания большие затраты на такого рода эксперимент: возможно усилия могли бы затрачиваться с большей пользой, если бы проводились проверки по интервалам, как это описано в ГОСТ Р ИСО 5725-6. Если повторяемость метода измерений низка, то будет практически невозможно достичь высокой степени определенности в оценке систематической погрешности лаборатории.
5.2 Ссылки на ГОСТ Р ИСО 5725-1 и ГОСТ Р ИСО 5725-2
При чтении частей 1 и 2 ГОСТ Р ИСО 5725 в контексте части 4 вместо терминов «прецизионность» или «повторяемость и воспроизводимость» следует употреблять термин «правильность». Применительно к ГОСТ Р ИСО 5725-2 количество лабораторий составит p = 1, и это может оказаться удобным в том смысле, что один человек может сочетать в себе «исполнителя» и «инспектора».
5.3 Количество результатов измерений
Неопределенность в оценке систематической погрешности лабораторий при реализации конкретного метода измерений зависит от повторяемости метода измерений и количества полученных результатов измерений.
Для того, чтобы в итоге эксперимента можно было с высокой вероятностью обнаружить установленное заранее значение систематической погрешности результатов измерений в лаборатории (см. приложение С), число результатов измерений n должно удовлетворять следующему неравенству
где Dm - заданное значение систематической погрешности лаборатории, которое хочет обнаружить экспериментатор по результатам эксперимента;
sr - стандартное отклонение повторяемости метода измерений и
5.4 Выбор стандартных образцов
В случае применения стандартного образца здесь также применяют требования, описанные в 4.2.1.
5.5 Статистический анализ
5.5.1 Проверка внутрилабораторного стандартного отклонения
Рассчитывают
среднее значение ![]() n результатов измерений и sW, а также оценку
внутрилабораторного стандартного отклонения sW, используя
следующие формулы:
n результатов измерений и sW, а также оценку
внутрилабораторного стандартного отклонения sW, используя
следующие формулы:
![]() (21)
(21)
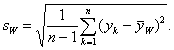 (22)
(22)
Результаты измерений должны быть тщательно исследованы на наличие выбросов с использованием критерия Граббса, как это описано в 7.3.4 ГОСТ Р ИСО 5725-2.
Если известно стандартное отклонение повторяемости sr для стандартного метода измерений, то оценка sW может быть получена по следующей процедуре.
Вычисляют отношение
![]()
![]() (23)
(23)
и сравнивают его с критическим значением
![]()
где ![]() представляет собой (1
- a)-квантиль c2-распределения с
n [ = п - 1] степенями свободы. Если не
установлено иначе, то a принимают
равным 0,05.
представляет собой (1
- a)-квантиль c2-распределения с
n [ = п - 1] степенями свободы. Если не
установлено иначе, то a принимают
равным 0,05.
a) Если C" £ C"crit, то sW не значимо больше sr.
b) Если C" > C"crit, то sW значимо больше sr.
В первом случае для оценки систематической погрешности лаборатории используют стандартное отклонение повторяемости sr метода измерений.
В последнем случае необходимо рассмотреть вопрос о повторении эксперимента с подтверждением на всех стадиях, что стандартный метод измерений реализуется надлежащим образом.
5.5.2 Оценка систематической погрешности лаборатории при реализации стандартного метода измерений
Оценку
![]() , систематической погрешности лаборатории D определяют по
формуле
, систематической погрешности лаборатории D определяют по
формуле
![]() (24)
(24)
Вариация оценки систематической погрешности лаборатории является следствием изменчивости результатов измерительного процесса, ее выражают как стандартное отклонение, определяемое следующим образом
![]() (25)
(25)
в случае известного значения стандартного отклонения повторяемости, или
![]() (26)
(26)
в случае, когда значение стандартного отклонения повторяемости неизвестно.
95 %-ный доверительный интервал систематической погрешности лаборатории определяется неравенством
![]() (27)
(27)
где AW рассчитывают по формуле (20).
Если sr неизвестно, то вместо него должна быть использована его оценка sr.
Если доверительный интервал включает в себя нулевое значение, систематическая погрешность лаборатории на уровне значимости a = 5 % незначима; в противном случае ее следует считать значимой.
Систематическая погрешность лаборатории при реализации стандартного метода измерений более детально рассматривается в ГОСТ Р ИСО 5725-6.
6 Доклад совету экспертов и решения, им принимаемые
6.1 Доклад эксперта по статистике
Завершив статистический анализ, эксперт по статистике должен составить доклад и представить его на рассмотрение совету экспертов.
В докладе должна быть представлена следующая информация:
a) полный перечень наблюдений, полученных от операторов и/или инспекторов, имеющих отношение к стандартному методу измерений;
b) полный перечень лабораторий, которые были исключены как выпадающие лаборатории, с указанием причин их исключения;
c) полный перечень квазивыбросов и/или выбросов, которые были обнаружены, с пояснениями, были ли они объяснены и исправлены или исключены;
d) конечные результаты соответствующих средних значений и показателей прецизионности (в виде таблицы);
e) выводы, является ли значимой систематическая погрешность стандартного метода измерений по отношению к используемому принятому опорному значению; если да, то в доклад должны быть внесены оценки систематической погрешности для каждого уровня.
6.2 Решения совета экспертов
Совет экспертов должен обсудить доклад эксперта по статистике и принять решения по следующим вопросам.
a) Являются ли несогласующиеся результаты измерений следствием недостатков в описании метода измерений?
b) Какие меры должны быть приняты в отношении выпадающих лабораторий?
c) Указывают ли результаты выпадающих лабораторий и/или комментарии, полученные от операторов и инспекторов, на необходимость усовершенствования стандартного метода измерений? Если да, то какие усовершенствования требуются?
d) Подтверждают ли результаты эксперимента по оценке точности приемлемость метода измерений для его признания в качестве стандартного? Какие меры предполагается принять относительно его опубликования?
7 Использование данных о правильности
Согласно разделу 7 ГОСТ Р ИСО 5725-1.
ПРИЛОЖЕНИЕ А
Условные обозначения и сокращения, используемые в ГОСТ Р ИСО 5725
a Отсекаемый на оси ординат отрезок в соотношении s = a + bm
A Показатель, используемый для расчета неопределенности оценки
b Угловой коэффициент прямой в соотношении s = a + bm
B Лабораторная составляющая систематической погрешности измерений при реализации конкретного метода - разность между систематической погрешностью лаборатории при реализации конкретного метода измерений (конкретной МВИ) и систематической погрешностью метода измерений
B0 Составляющая величины B, представляющая все факторы, которые не изменяются в условиях промежуточной прецизионности
B(1), B(2) и т.д. Составляющие величины B, представляющие факторы, которые изменяются в условиях промежуточной прецизионности
c Отсекаемый на оси ординат отрезок в соотношении lgs = c + dlgm
C, C¢, C" Тестовые статистики
Ccrit, C¢crit, C"сrit Критические значения для статистик
CDp Критическая разность для вероятности P
CRp Критический диапазон для вероятности P
d Угловой коэффициент прямой в соотношении lgs = c + dlgm
e Составляющая результата измерений, представляющая случайную погрешность каждого результата измерений
f Коэффициент критического диапазона
Fp(n1, n2) р-квантиль F-распределения с n1 и n2 степенями свободы
G Статистика Граббса
h Статистика Манделя для межлабораторной совместимости
k Статистика Манделя для внутрилабораторной совместимости
LCL Нижний предел контроля (действия либо предупреждения)
m Общее среднее значение измеряемой характеристики; уровень
M Количество факторов, рассматриваемых в условиях промежуточной прецизионности
N Количество повторений (итераций)
n Количество результатов измерений, полученных в одной лаборатории на одном уровне (т.е. в пределах ячейки - базового элемента)
p Количество лабораторий, участвующих в межлабораторном эксперименте
P Вероятность
q Количество уровней измеряемой характеристики в межлабораторном эксперименте
r Предел повторяемости (сходимости)
R Предел воспроизводимости
RM Стандартный образец
s Оценка стандартного отклонения
![]() Прогнозируемое
стандартное отклонение
Прогнозируемое
стандартное отклонение
T Итог или сумма какого-либо выражения
t Количество объектов испытаний или групп обектов
UCL Верхний предел контроля (действия либо предупреждения)
W Весовой коэффициент, используемый при расчете взвешенной регрессии
w Диапазон изменения выборки результатов измерений
x Заданная величина, используемая для критерия Граббса
y Результат измерений (испытаний)
![]() Среднее арифметическое
значение результатов измерений (испытаний)
Среднее арифметическое
значение результатов измерений (испытаний)
![]() Общее среднее
значение результатов измерений (испытаний)
Общее среднее
значение результатов измерений (испытаний)
a Уровень значимости
b Вероятность ошибки второго рода
g Отношение стандартного отклонения воспроизводимости к стандартному отклонению повторяемости (сходимости) (sR/sr)
D Систематическая погрешность лаборатории при реализации конкретного стандартного метода измерений (конкретной МВИ)
![]() Оценка
Д
Оценка
Д
d Систематическая погрешность метода измерений
![]() Оценка
d
Оценка
d
l Поддающаяся обнаружению разность между систематическими погрешностями двух лабораторий при реализации одного и того же метода измерений или систематическими погрешностями двух методов измерений (МВИ) одного и того же назначения на идентичных образцах
m Истинное или принятое опорное значение измеряемой величины (характеристики)
n Число степеней свободы
r Поддающееся обнаружению соотношение между стандартными отклонениями повторяемости (сходимости) для методов В и А
s Истинное (действительное) значение стандартного отклонения
t Составляющая результата измерений, представляющая изменение, обусловленное временем, прошедшим с момента последней калибровки
j Поддающееся обнаружению соотношение между квадратными корнями из межлабораторных средних квадратов для методов В и А
![]() p-квантиль c2-распределения с
n степенями
свободы
p-квантиль c2-распределения с
n степенями
свободы
Символы, используемые в качестве подстрочных индексов
C Различие, определяемое калибровкой
E Различие, определяемое оборудованием
i Идентификатор для конкретной лаборатории
I() Идентификатор для промежуточных мер прецизионности; в скобках - идентификация типа промежуточной ситуации
j Идентификатор для уровня (ГОСТ Р ИСО 5725-2)
Идентификатор для группы испытаний или для фактора (ГОСТ Р ИСО 5725-3)
k Идентификатор для конкретного результата испытаний в лаборатории i на уровне j
L Межлабораторный
m Идентификатор для поддающейся обнаружению систематической погрешности
M Различие, обусловленное неидентичностью проб (образцов)
O Различие, определяемое сменой оператора
P Вероятность
r Повторяемость
R Воспроизводимость
T Различие, обусловленное периодом (временем), в течение которого проводят измерения или оценочный эксперимент
W Внутрилабораторный
1, 2, 3... Для результатов измерений, нумеруемых в порядке их получения
(1), (2), (3)... Для результатов измерений (испытаний), нумеруемых в порядке возрастания измеряемой величины
ПРИЛОЖЕНИЕ В
(справочное)
Пример эксперимента по оценке точности
В.1 Описание эксперимента
Эксперимент по оценке точности определения содержания марганца в железных рудах методом атомной абсорбции проводился Техническим комитетом ИСО/ТК 102 «Железные руды» с использованием пяти исследуемых образцов с принятыми опорными значениями (m), приведенными в таблице В.1 (эти значения лабораториям не сообщались). Каждая лаборатория получила для каждого уровня по две наугад отобранные колбы с исследуемой пробой и провела параллельные анализы из каждой колбы. Две колбы использовались для подтверждения отсутствия различий между ними. Анализы были выполнены таким образом, чтобы в случае отсутствия различий между колбами четыре результата анализа могли быть признаны полученными в условиях повторяемости. Анализ результатов показал, что различие между колбами действительно было несущественным; пробы были признаны гомогенными. Такие результаты от каждой лаборатории могут быть признаны параллельными определениями в условиях повторяемости. Результаты анализов представлены в таблице В.2. Средние значения по лабораториям и дисперсии для каждого из пяти исследуемых образцов представлены в таблице В.3.
В.2 Оценка прецизионности
С целью оценки прецизионности химико-аналитического метода данные были подвергнуты анализу согласно процедуре, описанной в ГОСТ Р ИСО 5725-2. Результаты измерений для каждого уровня представлены на рисунках В.1 - В.5.
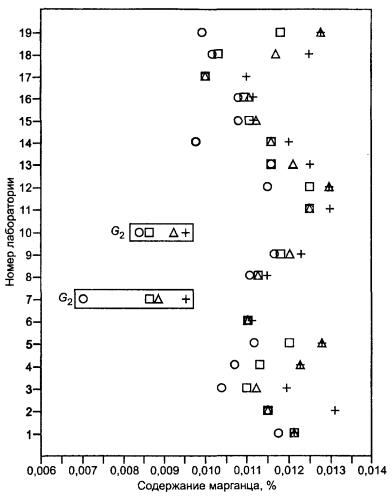
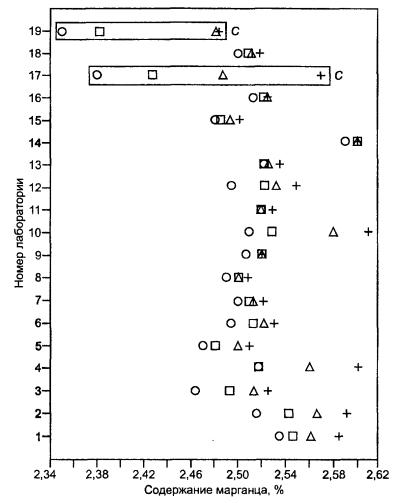
Квазивыбросы и выбросы как для критерия Кохрена, так и для критерия Граббса были идентифицированы и сведены в таблицу В.4. Точки на рисунках В.1 - В.5 в прямоугольных рамках означают, что соответствующие результаты измерений были идентифицированы как выбросы. Таблица В.4 демонстрирует, что в качестве выбросов были идентифицированы семь результатов; среди них пять принадлежали двум лабораториям (№ 10 и № 19). Один результат был идентифицирован как квазивыброс; он принадлежал той же лаборатории (№ 10).
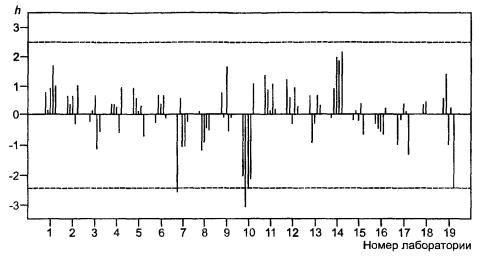
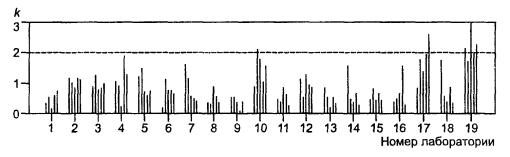
Значения статистик h и k представлены на рисунках В.6 и В.7. Значения h (рисунок В.6) отчетливо свидетельствуют, что лаборатория № 10 получает очень низкие результаты; два из них (уровни 2 и 3) были идентифицированы как выбросы. По этой причине было решено полностью исключить результаты лаборатории № 10; это должно бы стать предметом особого рассмотрения и принятия необходимых мер. Кроме того, были отбракованы данные на уровне 1 в лаборатории № 7, идентифицированные как выброс согласно критерию Граббса. Значения k (рисунок В.7) свидетельствуют о том, что лаборатории № 10, № 17 и № 19 имеют тенденцию к получению несколько более высокой внутрилабораторной вариации по сравнению с остальными. Здесь опять же необходимо принять соответствующие меры в форме обследования этих лабораторий или, в случае необходимости, в форме ужесточения процедуры выполнения измерений. Было также решено отбраковать выбросы, идентифицированные согласно критерию Кохрена; т.е. данные на уровнях 3 и 5 в лаборатории № 19 и на уровне 5 в лаборатории № 17.
Затем на основе оставшихся данных были рассчитаны стандартные отклонения повторяемости и воспроизводимости. Результаты расчета суммированы в таблице В.5 и представлены в виде графика в функции уровня на рисунке В.8. Рисунок В.8 свидетельствует о том, что имеет место линейная зависимость показателей прецизионности от уровня концентрации, причем соответствующие уравнения линейной регрессии стандартных отклонений повторяемости и воспроизводимости в функции от уровней концентрации выглядят следующим образом:
sr = 0,000579 + 0,00885m,
sr = 0,000737 + 0,01557m.
В.3 Оценка правильности
Правильность метода измерений была оценена путем расчета 95 %-ных доверительных интервалов систематической погрешности метода с использованием соотношения (19) и определения положения этих интервалов относительно нуля (таблица В.5). Поскольку на уровнях 3 - 5 эти доверительные интервалы охватывают нулевое значение, систематическая погрешность данного метода измерений не является значимой на уровнях высоких концентраций марганца 3 - 5; поскольку на уровнях 1 и 2 доверительные интервалы не охватывают нулевого значения, систематическая погрешность является значимой на уровнях низких концентраций 1 и 2.
В.4 Дальнейший анализ
Из
исходных данных может быть получена более подробная информация посредством
выполнения дополнительного анализа, такого как регрессионный анализ для ![]() в функции от m.
в функции от m.
Таблица В.1 - Содержание марганца в железных рудах. Принятые опорные значения
|
1 |
2 |
3 |
4 |
5 |
|
|
Принятое опорное значение m, % Mn |
0,0100 |
0,0930 |
0,4010 |
0,7770 |
2,5300 |
Таблица В.2 - Содержание марганца в железных рудах. Результаты анализа, в процентах Mn
|
Номер колбы |
Уровень |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
|||||||
|
1 |
1 |
0,0118 |
0,0121 |
0,0880 |
0,0875 |
0,408 |
0,407 |
0,791 |
0,791 |
2,584 |
2,560 |
|
2 |
0,0121 |
0,0121 |
0,0865 |
0,0867 |
0,407 |
0,408 |
0,794 |
0,801 |
2,535 |
2,545 |
|
|
2 |
1 |
0,0131 |
0,0115 |
0,0894 |
0.0861 |
0,411 |
0,405 |
0,760 |
0,766 |
2,543 |
2,591 |
|
2 |
0,0115 |
0,0115 |
0,0887 |
0,0867 |
0,406 |
0,399 |
0,766 |
0,783 |
2,516 |
2,567 |
|
|
3 |
1 |
0,0118 |
0,0112 |
0,0864 |
0,0849 |
0,410 |
0,403 |
0,752 |
0,767 |
2,526 |
2,463 |
|
2 |
0,0110 |
0,0104 |
0,0867 |
0,0896 |
0,408 |
0,400 |
0,755 |
0,753 |
2,515 |
2,493 |
|
|
4 |
1 |
0,0107 |
0,0121 |
0,0881 |
0,0892 |
0,402 |
0,402 |
0,780 |
0,750 |
2,560 |
2,520 |
|
2 |
0,0114 |
0,0121 |
0,0861 |
0,0874 |
0,404 |
0,402 |
0,777 |
0,750 |
2,600 |
2,520 |
|
|
5 |
1 |
0,0120 |
0,0128 |
0,0904 |
0,0904 |
0,404 |
0,400 |
0,775 |
0,775 |
2,470 |
2,510 |
|
2 |
0,0112 |
0,0128 |
0,0862 |
0,0870 |
0,404 |
0,396 |
0,770 |
0,780 |
2,500 |
2,480 |
|
|
6 |
1 |
0,0111 |
0,0110 |
0,0892 |
0,0893 |
0,402 |
0,398 |
0,786 |
0,782 |
2,531 |
2,514 |
|
2 |
0,0110 |
0,0111 |
0,0900 |
0,0864 |
0,408 |
0,404 |
0,780 |
0,772 |
2,524 |
2,494 |
|
|
7 |
1 |
0,0088 |
0,0095 |
0,0893 |
0,0895 |
0,390 |
0,390 |
0,754 |
0,762 |
2,510 |
2,521 |
|
2 |
0,0070 |
0,0086 |
0,0859 |
0,0886 |
0,395 |
0,395 |
0,758 |
0,756 |
2,500 |
2,513 |
|
|
8 |
1 |
0,0115 |
0,0112 |
0,0823 |
0,0823 |
0,390 |
0,396 |
0,761 |
0,765 |
2,501 |
2,499 |
|
2 |
0,0113 |
0,0113 |
0,0828 |
0,0829 |
0,400 |
0,389 |
0,770 |
0,766 |
2,507 |
2,490 |
|
|
9 |
1 |
0,0123 |
0,0120 |
0,0862 |
0,0866 |
0,414 |
0,414 |
0,765 |
0,765 |
2,523 |
2,520 |
|
2 |
0,0117 |
0,0118 |
0,0865 |
0,0876 |
0,411 |
0,414 |
0,765 |
0,765 |
2,521 |
2,508 |
|
|
10 |
1 |
0,0095 |
0,0086 |
0,0780 |
0,0720 |
0,390 |
0,370 |
0,746 |
0,730 |
2,530 |
2,580 |
|
2 |
0,0092 |
0,0084 |
0,0780 |
0,0730 |
0,392 |
0,374 |
0,750 |
0,738 |
2,510 |
2,610 |
|
|
11 |
1 |
0,0125 |
0,0125 |
0,0900 |
0,0890 |
0,405 |
0,395 |
0,790 |
0,780 |
2,520 |
2,520 |
|
2 |
0,0130 |
0,0125 |
0,0890 |
0,0895 |
0,400 |
0,405 |
0,785 |
0,790 |
2,530 |
2,520 |
|
|
12 |
1 |
0,0125 |
0,0130 |
0,0885 |
0,0890 |
0,405 |
0,395 |
0,790 |
0,780 |
2,535 |
2,525 |
|
2 |
0,0115 |
0,0130 |
0,0890 |
0,0875 |
0,405 |
0,390 |
0,775 |
0,790 |
2,550 |
2,495 |
|
|
13 |
1 |
0,0125 |
0,0116 |
0,0842 |
0,0832 |
0,399 |
0,399 |
0,784 |
0,777 |
2,523 |
2,523 |
|
2 |
0,0121 |
0,0116 |
0,0832 |
0,0828 |
0,398 |
0,399 |
0,782 |
0,777 |
2,527 |
2,537 |
|
|
14 |
1 |
0,0116 |
0,0120 |
0,0898 |
0,0890 |
0,418 |
0,416 |
0,797 |
0,800 |
2,602 |
2,602 |
|
2 |
0,0098 |
0,0116 |
0,0900 |
0,0902 |
0,415 |
0,415 |
0,801 |
0,790 |
2,592 |
2,602 |
|
|
15 |
1 |
0,0108 |
0,0112 |
0,0871 |
0,0860 |
0,399 |
0,400 |
0,775 |
0,774 |
2,488 |
2,495 |
|
2 |
0,0112 |
0,0111 |
0,0883 |
0,0861 |
0,397 |
0,401 |
0,783 |
0,773 |
2,503 |
2,485 |
|
|
16 |
1 |
0,0109 |
0,0108 |
0,0846 |
0,0858 |
0,392 |
0,400 |
0,779 |
0,769 |
2,528 |
2,516 |
|
2 |
0,0111 |
0,0110 |
0,0849 |
0,0855 |
0,396 |
0,397 |
0,751 |
0,753 |
2,528 |
2,525 |
|
|
17 |
1 |
0,0100 |
0,0110 |
0,0849 |
0,0880 |
0,409 |
0,410 |
0,766 |
0,794 |
2,571 |
2,380 |
|
2 |
0,0100 |
0,0100 |
0,0830 |
0,0890 |
0,392 |
0,402 |
0,755 |
0,775 |
2,429 |
2,488 |
|
|
18 |
1 |
0,0117 |
0,0102 |
0,0880 |
0,0881 |
0,405 |
0,404 |
0,771 |
0,773 |
2,520 |
2,511 |
|
2 |
0,0125 |
0,0103 |
0,0868 |
0,0882 |
0,402 |
0,403 |
0,778 |
0,763 |
2,514 |
2,503 |
|
|
19 |
1 |
0,0099 |
0,0128 |
0,0945 |
0,0905 |
0,398 |
0,375 |
0,770 |
0,767 |
2,483 |
2,351 |
|
2 |
0,0118 |
0,0128 |
0,0924 |
0,0884 |
0,418 |
0,382 |
0,799 |
0,760 |
2,485 |
2,382 |
|
Таблица В.3 - Содержание марганца в железных рудах. Лабораторные средние значения и лабораторные дисперсии
|
Уровень |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
Лабораторное среднее значение |
|||||
|
1 |
0,01203 |
0,08718 |
0,40750 |
0,79425 |
2,55600 |
|
2 |
0,01190 |
0,08773 |
0,40525 |
0,76875 |
2,55425 |
|
3 |
0,01110 |
0,08690 |
0,40525 |
0,75675 |
2,49925 |
|
4 |
0,01158 |
0,08770 |
0,40250 |
0,76425 |
2,55000 |
|
5 |
0,01220 |
0,08850 |
0,40100 |
0,77500 |
2,49000 |
|
6 |
0,01105 |
0,08873 |
0,40300 |
0,78000 |
2,51575 |
|
7 |
0,00848 |
0,08833 |
0,39250 |
0,75750 |
2,51100 |
|
8 |
0,01133 |
0,08258 |
0,39375 |
0,76550 |
2,49925 |
|
9 |
0,01195 |
0,08673 |
0,41325 |
0,76500 |
2,51800 |
|
10 |
0,00893 |
0,07525 |
0,38150 |
0,74100 |
2,55750 |
|
11 |
0,01263 |
0,08938 |
0,40125 |
0,78625 |
2,52250 |
|
12 |
0,01250 |
0,08850 |
0,39875 |
0,78375 |
2,52625 |
|
13 |
0,01195 |
0,08335 |
0,39875 |
0,78000 |
2,52750 |
|
14 |
0,01125 |
0,08975 |
0,41600 |
0,79700 |
2,59950 |
|
15 |
0,01108 |
0,08688 |
0,39925 |
0,77625 |
2,49275 |
|
16 |
0,01095 |
0,08520 |
0,39625 |
0,76300 |
2,52425 |
|
17 |
0,01025 |
0,08623 |
0,40325 |
0,77250 |
2,46700 |
|
18 |
0,01118 |
0,08778 |
0,40350 |
0,77125 |
2,51200 |
|
19 |
0,01183 |
0,09145 |
0,39325 |
0,77400 |
2,42525 |
|
Лабораторная дисперсия |
|||||
|
1 |
0,2250 ´ 10-7 |
0,4892 ´ 10-6 |
0,3333 ´ 10-6 |
0,2225 ´ 10-4 |
0,4540 ´ 10-3 |
|
2 |
0,6400 ´ 10-6 |
0,2482 ´ 10-5 |
0,2425 ´ 10-4 |
0,9825 ´ 10-4 |
0,1034 ´ 10-2 |
|
3 |
0,3333 ´ 10-6 |
0,3860 ´ 10-5 |
0,2092 ´ 10-4 |
0,4825 ´ 10-4 |
0,7722 ´ 10-3 |
|
4 |
0,4492 ´ 10-6 |
0,1687 ´ 10-5 |
0,1000 ´ 10-5 |
0,2722 ´ 10-3 |
0,1467 ´ 10-2 |
|
5 |
0,5867 ´ 10-6 |
0,4920 ´ 10-5 |
0,1467 ´ 10-4 |
0,1667 ´ 10-4 |
0,3333 ´ 10-3 |
|
6 |
0,3333 ´ 10-8 |
0,2529 ´ 10-5 |
0,1733 ´ 10-4 |
0,3467 ´ 10-4 |
0,2589 ´ 10-3 |
|
7 |
0,1116 ´ 10-5 |
0,2763 ´ 10-5 |
0,8333 ´ 10-5 |
0,1167 ´ 10-4 |
0,7533 ´ 10-4 |
|
8 |
0,1583 ´ 10-7 |
0,1025 ´ 10-6 |
0,2692 ´ 10-4 |
0,1367 ´ 10-4 |
0,4958 ´ 10-4 |
|
9 |
0,7000 ´ 10-7 |
0,3692 ´ 10-6 |
0,2250 ´ 10-5 |
0 |
0,4600 ´ 10-4 |
|
10 |
0,2625 ´ 10-6 |
0,1025 ´ 10-4 |
0,1237 ´ 10-3 |
0,7867 ´ 10-4 |
0,2092 ´ 10-3 |
|
11 |
0,6250 ´ 10-7 |
0,2292 ´ 10-6 |
0,2292 ´ 10-4 |
0,2292 ´ 10-4 |
0,2500 ´ 10-4 |
|
12 |
0,5000 ´ 10-6 |
0,5000 ´ 10-6 |
0,5625 ´ 10-4 |
0,5625 ´ 10-4 |
0,5396 ´ 10-2 |
|
13 |
0,1900 ´ 10-6 |
0,3567 ´ 10-6 |
0,2500 ´ 10-6 |
0,1267 ´ 10-4 |
0,4367 ´ 10-4 |
|
14 |
0,9700 ´ 10-6 |
0,2767 ´ 10-6 |
0,2000 ´ 10-5 |
0,2467 ´ 10-4 |
0,2500 ´ 10-4 |
|
15 |
0,3583 ´ 10-7 |
0,1149 ´ 10-5 |
0,2917 ´ 10-5 |
0,2092 ´ 10-4 |
0,6425 ´ 10-4 |
|
16 |
0,1667 ´ 10-7 |
0,3000 ´ 10-6 |
0,1092 ´ 10-4 |
0,1787 ´ 10-3 |
0,3225 ´ 10-4 |
|
17 |
0,2500 ´ 10-6 |
0,7669 ´ 10-5 |
0,6892 ´ 10-4 |
0,2723 ´ 10-3 |
0,6757 ´ 10-2 |
|
18 |
0,1249 ´ 10-5 |
0,4292 ´ 10-6 |
0,1667 ´ 10-5 |
0,3892 ´ 10-4 |
0,5000 ´ 10-4 |
|
19 |
0,1869 ´ 10-5 |
0,6803 ´ 10-5 |
0,3649 ´ 10-3 |
0,2953 ´ 10-3 |
0,4763 ´ 10-2 |
Таблица В.4 - Содержание марганца в железных рудах. Выбросы и квазивыбросы
|
Номер лаборатории |
Вычисленная статистика1 |
Критическое значение статистики |
|
|
Перечень выбросов (a = 0,01) |
|||
|
1 |
7 |
G2 = 0,295 |
G2(19) = 0,3398 |
|
|
10 |
|
|
|
2 |
10 |
G1 = 3,305 |
G1(19) = 2,968 |
|
3 |
19 |
C = 0,474 |
C(4, 19) = 0,276 |
|
|
10 |
C = 0,305 |
C(4, 18) = 0,288 |
|
4 |
- |
- |
- |
|
5 |
17 |
C = 0,358 |
C(4, 19) = 0,276 |
|
|
19 |
C = 0,393 |
C(4, 18) = 0,288 |
|
Перечень квазивыбросов (a = 0,05) |
|||
|
1 |
- |
- |
- |
|
2 |
- |
- |
- |
|
3 |
- |
- |
- |
|
4 |
- |
- |
- |
|
5 |
10 |
C = 0,284 |
C(4, 17) = 0,250 |
|
С - критерий Кохрена; G1 - критерий Граббса для одного выброса; G2 - критерий Граббса для двух выбросов. |
|||
Таблица В.5 - Содержание марганца в железных рудах. Оценка стандартных отклонений повторяемости, воспроизводимости и систематической погрешности метода измерений
|
Уровень |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
n |
4 |
4 |
4 |
4 |
4 |
|
p |
17 |
18 |
17 |
18 |
16 |
|
sr |
0,00065 |
0,00143 |
0,00407 |
0,00895 |
0,01815 |
|
sR |
0,00084 |
0,00248 |
0,00706 |
0,01385 |
0,03246 |
|
g |
1,29 |
1,73 |
1,73 |
1,54 |
1,79 |
|
A |
0,3528 |
0,3999 |
0,4117 |
0,3830 |
0,4287 |
|
AsR |
0,000296 |
0,000991 |
0,002906 |
0,005301 |
0,013916 |
|
|
0,0116 |
0,0874 |
0,4024 |
0,7739 |
2,5249 |
|
m |
0,0100 |
0,0930 |
0,4010 |
0,7770 |
2,5300 |
|
|
0,0016 |
-0,0056 |
0,0014 |
-0,0031 |
-0,0051 |
|
|
0,0013 |
-0,0066 |
-0,0015 |
-0,0084 |
-0,0190 |
|
|
0,0019 |
-0,0046 |
0,0043 |
0,0022 |
0,0088 |
|
* Условные обозначения см. в приложении А. |
|||||
Примечание - Точки в прямоугольных рамках означают, что соответствующие результаты измерений были идентифицированы как выбросы согласно критерию Граббса для двух выбросов (G2).
Рисунок В.1 - Содержание марганца в железных рудах. Результаты измерений на уровне 1
Примечание - Точки в прямоугольной рамке означают, что соответствующие результаты измерений были идентифицированы как выбросы согласно критерию Граббса для одного выброса (G1).
Рисунок В.2 - Содержание марганца в железных рудах. Результаты измерений на уровне 2
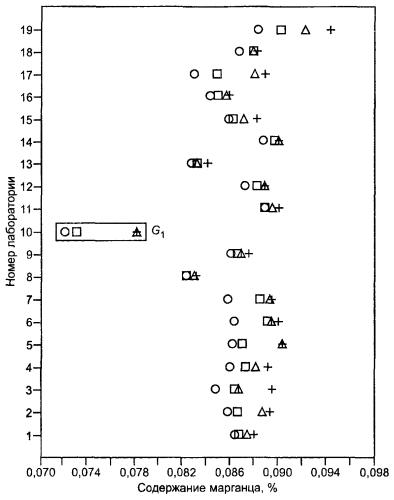
Примечание - Точки в прямоугольных рамках означают, что соответствующие результаты измерений были идентифицированы как выбросы согласно критерию Кохрена (C).
Рисунок В.3 - Содержание марганца в железных рудах. Результаты измерений на уровне 3
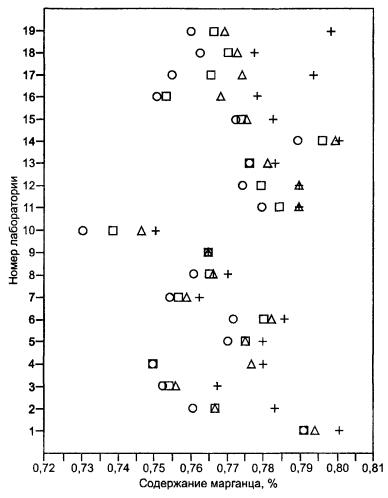
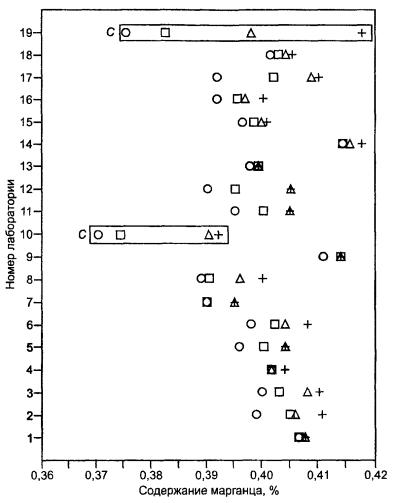
Рисунок В.4 - Содержание марганца в железных рудах. Результаты измерений на уровне 4
Примечание - Точки в прямоугольных рамках означают, что результаты измерений были идентифицированы как выбросы согласно критерию Кохрена (C).
Рисунок В.5 - Содержание марганца в железных рудах. Результаты измерений на уровне 5
Рисунок В.6 - Содержание марганца в железных рудах. Значения h, сгруппированные по лабораториям
Рисунок В.7 - Содержание марганца в железных рудах. Значения k, сгруппированные по лабораториям
Рисунок В.8 - Содержание марганца в железных рудах. Стандартные отклонения повторяемости и воспроизводимости как линейные функции уровня концентрации m
ПРИЛОЖЕНИЕ С
(справочное)
Вывод соотношений
С.1. Формулы (5) и (6) (см. 4.5)
Минимальное количество лабораторий p и результатов измерений n вычисляют, исходя из требований удовлетворения двух следующих условий:
a) измерение должно сделать возможным обнаружение, что систематическая погрешность равна нулю с вероятностью 1 - a = 0,95;
b) измерение должно сделать возможным обнаружение ожидаемого значения систематической погрешности dm с вероятностью 1 - b = 0,95.
Первое условие развито согласно 4.7.2, где доверительный интервал для систематической погрешности метода измерений d использован для выполнения статистической проверки гипотезы, что систематическая погрешность равна нулю (H0: d = 0), альтернативно гипотезе, что систематическая погрешность не равна нулю (H1: d ¹ 0).
Эквивалентной
формой этой проверки является сравнение абсолютного значения оценки
систематической погрешности метода измерений ![]() с критическим значением K и отклонением
гипотезы H0 (d = 0), если
с критическим значением K и отклонением
гипотезы H0 (d = 0), если ![]() (и принятием гипотезы H0 (d = 0), если
(и принятием гипотезы H0 (d = 0), если ![]() ).
).
K может быть вычислена, используя требование, что вероятность отклонения гипотезы H0, если она истинна, должна быть равна выбранному уровню значимости a = 5 %:
![]()
Найдем критическое значение K на основе соотношений:
где Ф() - интегральная функция распределения стандартного нормального распределения;
up - p-квантиль стандартного нормального распределения;
![]() - дисперсия оценки
систематической погрешности метода измерений:
- дисперсия оценки
систематической погрешности метода измерений:
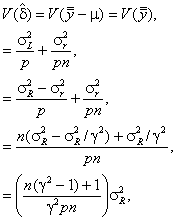
где g = sR/sr, а sl2 представляет собой межлабораторную дисперсию, так что sR2 = sL2 + sr2.
Для альтернативной гипотезы потребуем выполнения условия, при котором в результате эксперимента станет возможным определить ожидаемое значение систематической погрешности dm с вероятностью 1 - b = 0,95:
![]()
что дает
Приравняв два выражения (С.1 и С.2), для K получим
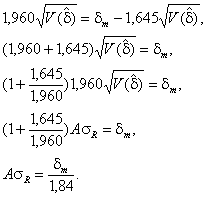
С.2 Формулы (19) и (20) (см. 5.3)
Данные
уравнения получаются сразу, если в предшествующем выводе (С.1) d, dm, ![]() ,
, ![]() и A заменить на D, Dm,
и A заменить на D, Dm, ![]() ,
, ![]() и AW соответственно,
а выражение для
и AW соответственно,
а выражение для ![]() заменить на
заменить на ![]()
ПРИЛОЖЕНИЕ D
(справочное)
Библиография
[2] ISO Guide 35: 1989. Certification of reference materials - General and statistical principles
Ключевые слова: измерение, испытания, метод измерений, стандартизация метода измерений, результаты измерений, результаты испытаний, точность, правильность, прецизионность, систематическая погрешность, повторяемость, воспроизводимость, случайная погрешность, эксперимент по оценке точности, альтернативный метод измерений, статистический анализ